1.公式推導
1.1兩個問題
ICA算法會帶來2個不確定性:
????????幅值不確定性和順序不確定性。
![]()
1.2 推導
觀測數據?x?是盲源?s 的線性混合:x?=?As? ??? ? ? ? ???(1)
![]()
????????此時,W矩陣是未知的,ICA算法的目的便是找到一個最優的矩陣W,實現對矩陣S^的求解。如果直接采用線性代數的方法對(2)式進行求解,顯然是不可行的。因此需要增加額外的條件讓(2)式更容易求解。
????????ICA算法通過假設Si 為兩兩相互獨立的隨機變量,由矩陣A變換后,成為兩兩非相互獨立的隨機變量Xi從而進行求解。這個條件也限制了Xi中最多只能有一個呈高斯分布的隨機變量,否則,就不能滿足Xi之間兩兩非相互獨立的條件。?
上文解釋:
????????當獨立的源信號?Si??被混合矩陣?A?線性組合后,得到的觀測信號?Xi??會失去獨立性,變成 “兩兩非相互獨立”。ICA 的求解邏輯就是 “源信號?Si??獨立 → 混合后?Xi??非獨立”,進行反向操作:
- 從觀測信號?X(非獨立)出發,假設它由 “獨立源?S?混合” 而來;
- 通過算法尋找一個 “解混矩陣?W”(即你提到的?W?矩陣 ),使得?W?X?的結果盡可能接近 “獨立的源信號?S”;
- 最終,當?W?X?恢復出 “兩兩獨立” 的特性時,就認為找到了源信號?S?的近似解?S^。
?為什么限制 “最多一個高斯分布”?
????????如果源信號?Si??中有兩個或以上是高斯分布,混合后的觀測信號?Xi??會因 “高斯分布的線性組合仍為高斯分布”,導致?Xi??之間的 “非獨立性” 無法區分(數學上,多個獨立高斯信號混合后,無法通過統計方法唯一解混 )。因此,ICA 要求源信號?Si??中最多一個是高斯分布,才能保證混合后的?Xi??有 “可解混” 的非獨立性。????????
限制一個高斯分布的證明過程:
????????已知高斯分布的概率密度函數是:
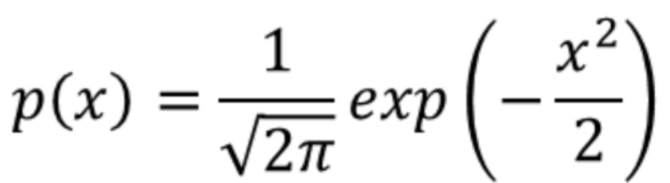
????????假設混合信號x1,x2都滿足高斯分布,其聯合概率分布函數可以寫成:
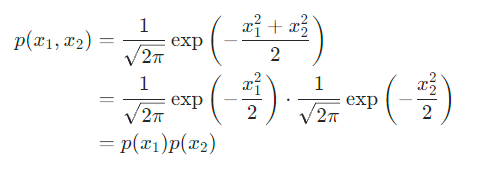
????????根據概率論中對相互獨立的定義,x1,x2相互獨立,從而無法滿足ICA算法中,混合信號xi之間兩兩非相互獨立的要求。
繼續證明:
????????ICA 算法的目的是得到兩兩相互獨立的Si?,因此需要對求解結果之間的獨立性進行評結,評估的方式是對結果的非高斯性進行量化評估。
????????根據 (3) 式,X由多獨立成分混合成的,為了簡化問題,假設這些獨立成分有相同的分布。現在考慮其中一個獨立成分的求解。

????????此時,y?可以視為?Si??的線性組合。根據中心極限定理 (多個獨立隨機變量的線性組合/或均值,其分布會隨著組合項數的增加,逐漸趨近于高斯分布),y?比任何一個?Si??都更加接近高斯分布。通過尋找一個?w,讓?wT·x?的高斯性盡可能的低,從而讓?y?接近某個?Si?,這是 ICA 算法的核心思路。最理想的情況是向量中只有一個非零值,此時,y?就等價于某個?s。
????????對隨機變量的非高斯性進行量化評價通常有以下幾種方法,假設隨機變量?y?的期望為 0,方差為 1。
1.3 評估隨機變量的非高斯性(峰度)
假設隨機變量的期望為0,方差為1
1.峰度
峰度定義為:
![]()
通過假設y的方差為 1,(8) 式可以簡化為:
![]()
若y符合高斯分布,則峰度kurt(y)=0,對于大多數非高斯隨機變量為非零值。
峰度有以下性質:對于兩個獨立的隨機變量x1?,x2?,有:
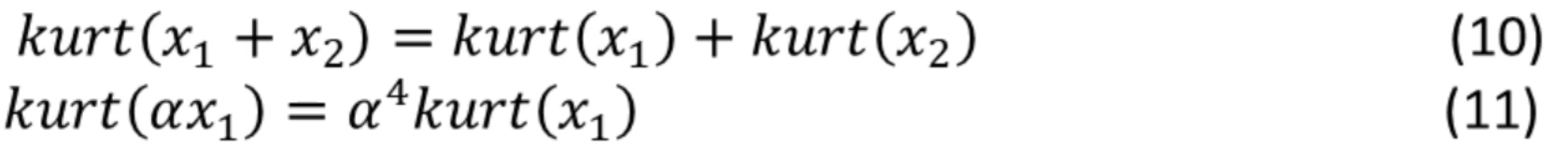
假設有獨立成分?s1?,s2?,有峰度?kurt(s1?),kurt(s2?),尋找其中的一個獨立成分y:
根據(式7),且![]() (獨立成分的方差為1,期望為0,Si的平方的期望為1)
(獨立成分的方差為1,期望為0,Si的平方的期望為1)
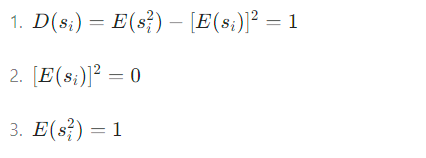
?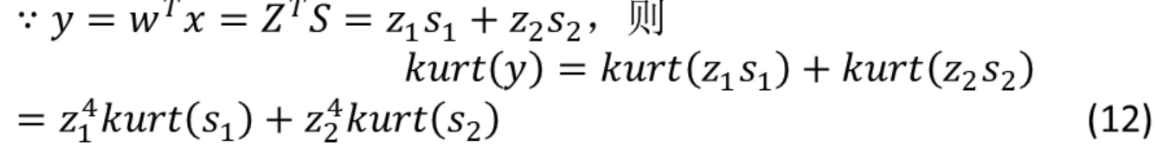
獨立成分的方差為1,期望為0,即
![]()
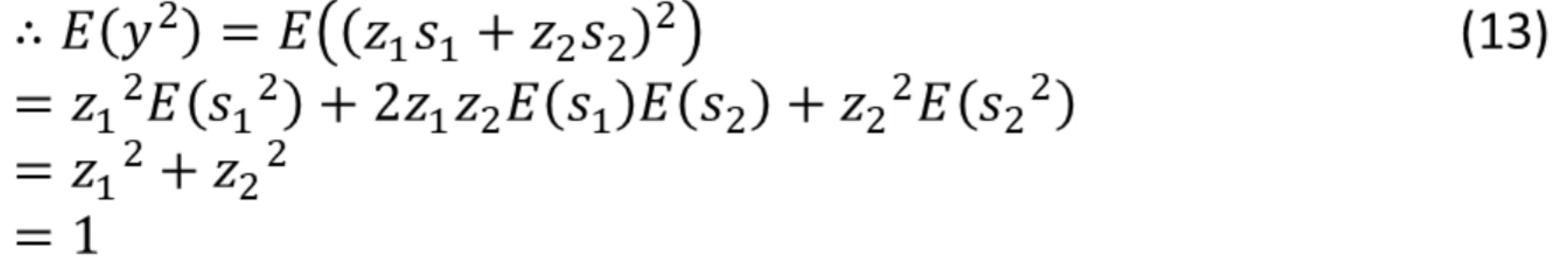
?由 (12) 式得:
![]()
????????通過讓 (14) 式的值最大化,減小y的高斯性。最理想的情況下,z1?,z2?中一個為 0,一個非零。此時,非零的zi?等于 1 或 - 1,y等價于某個±si?。
????????實際應用中,需要計算∣kurt(y)∣到最大值的梯度,從而迭代w的值,然而峰值并不是衡量高斯性的最好方法 。
1.4 評估隨機變量的非高斯性(負熵)
負熵定義:
![]()
其中,Ygaussian??是與?y?有相同協方差矩陣的隨機變量。
????????負熵總是非負的,當?y?是高斯分布時,負熵為 0。這是對高斯性的最佳衡量方式,缺點是計算復雜,因此可以使用一些近似的方法求負熵。??
1.4.1 高階矩
假設y期望為0,方差為1,則:
![]()
1.4.2 最大熵近似原理?
假設y期望為0,方差為1,則:
![]()
其中,v為高斯變量,G為非二次函數,需自行定義。一些比較好的G如下所示:
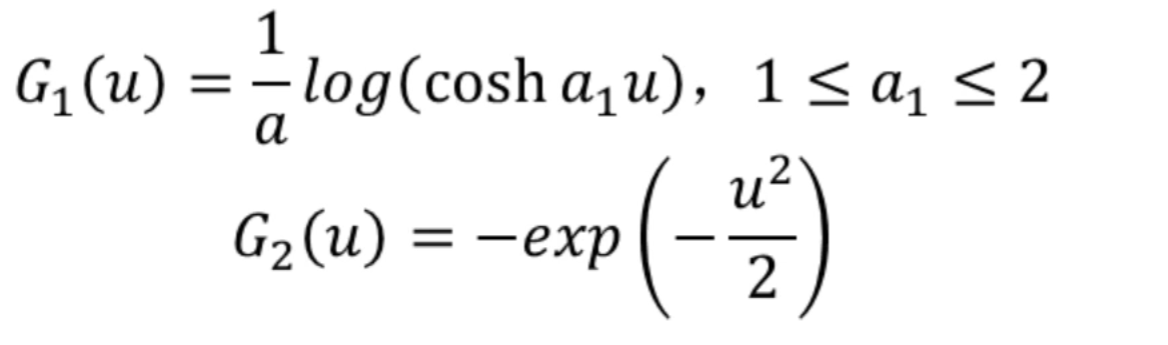
1.5 最小化互信息
見文 ICA學習(1)的?6.?最小化多重信息的簡化部分
總結:最下化互信息即最大化負熵。
2. ICA的預處理
2.1 中心化
????????中心化是非常基礎,也是很有必要的預處理過程。假設向量 x 的期望是 m,將向量 x 的所有元素減去 m,可以使向量 x 的均值變為 0。中心化可以表達為:
????????E(x?E(x))=0? ? ? ? ? ? ? ? ? ? (26)
)







![[數據庫]Neo4j圖數據庫搭建快速入門](http://pic.xiahunao.cn/[數據庫]Neo4j圖數據庫搭建快速入門)






)



