文章目錄
- 相機標定
- 目標
- 基礎原理
- 代碼
- 配置
- 校準
- 去畸變
- 1、使用 cv.undistort()
- 2、使用**重映射**方法
- 重投影誤差
- 練習
- 姿態估計
- 目標
- 基礎
- 渲染立方體
- 極線幾何
- 目標
- 基礎概念
- 代碼
- 練習
- 從立體圖像生成深度圖
- 目標
- 基礎概念
- 代碼
- 附加資源
- 練習
相機標定
https://docs.opencv.org/4.x/dc/dbb/tutorial_py_calibration.html
目標
在本節中,我們將學習以下內容:
- 由相機引起的畸變類型
- 如何找到相機的內參和外參屬性
- 如何基于這些屬性對圖像進行去畸變處理
基礎原理
某些針孔相機會對圖像引入明顯的畸變。主要有兩種畸變類型:徑向畸變和切向畸變。
徑向畸變會導致直線在圖像中呈現彎曲。距離圖像中心越遠的點,徑向畸變效應越顯著。例如下圖展示了一個標有紅線的棋盤兩邊緣,但可以看到棋盤邊框并非直線且與紅線不重合,所有本應筆直的線條都出現了外凸現象。更多細節可參考光學畸變。

后續章節將引入若干新參數,詳見相機標定與三維重建。
徑向畸變的數學模型如下:
\[x_{畸變} = x( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6) \\
y_{畸變} = y( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6)\]
切向畸變則是由于鏡頭與成像平面不完全平行所導致,使得圖像某些區域看起來比實際更近。其數學模型為:
\[x_{畸變} = x + [ 2p_1xy + p_2(r2+2x2)] \\
y_{畸變} = y + [ p_1(r^2+ 2y^2)+ 2p_2xy]\]
簡而言之,我們需要求解五個畸變系數:
\[畸變系數=(k_1 \hspace{10pt} k_2 \hspace{10pt} p_1 \hspace{10pt} p_2 \hspace{10pt} k_3)\]
此外還需獲取相機的內參和外參。內參是相機特有參數,包括焦距(\(f_x,f_y\))和光心坐標(\(c_x, c_y\))。這些參數可構成相機矩陣用于消除鏡頭畸變,該矩陣對于特定相機具有唯一性,計算后可重復用于同相機拍攝的其他圖像。其3x3矩陣形式為:
\[相機矩陣 = \left [ \begin{matrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{matrix} \right ]\]
外參則對應旋轉和平移向量,用于將三維點坐標轉換到特定坐標系。
在立體視覺應用中,需先校正這些畸變。為求解參數,需要提供已知圖案的樣本圖像(如棋盤格)。通過識別圖案中已知相對位置的特定點(如棋盤角點),結合這些點在現實空間和圖像中的坐標,即可解算畸變系數。為獲得理想結果,至少需要10組測試圖案。
代碼
如前所述,我們至少需要10個測試圖案來進行相機標定。OpenCV自帶了一些棋盤格圖像(參見 samples/data/left01.jpg – left14.jpg),因此我們將使用這些圖像。以一張棋盤格圖像為例,相機標定所需的關鍵輸入數據是:一組3D真實世界點坐標及其在圖像中對應的2D坐標點。我們可以輕松從圖像中獲取2D圖像點(這些圖像點是棋盤格中兩個黑色方塊相接的位置)。
那么真實世界空間中的3D點如何確定呢?這些圖像是由固定相機拍攝的,棋盤格被放置在不同位置和方向。因此我們需要知道\((X,Y,Z))坐標值。但為了簡化,我們可以假設棋盤格始終保持在XY平面(即Z恒為0),相機則相應移動。這種設定讓我們只需找出X,Y值。對于X,Y值,我們可以簡單地傳遞(0,0)、(1,0)、(2,0)等點坐標來表示位置。這種情況下,得到的結果將以棋盤格方塊的尺寸為比例單位。但如果我們知道方塊的實際尺寸(比如30毫米),就可以傳遞(0,0)、(30,0)、(60,0)等值,這樣結果將以毫米為單位(本例中由于我們未實際測量那些圖像的方塊尺寸,所以使用方塊尺寸作為單位)。
3D點被稱為對象點,2D圖像點則稱為圖像點。
配置
要在棋盤上尋找圖案,我們可以使用函數 cv.findChessboardCorners()。我們還需要指定要尋找的圖案類型,例如8x8網格、5x5網格等。本例中我們使用7x6網格(通常棋盤有8x8個方格和7x7個內部角點)。該函數會返回角點坐標和一個布爾值retval——若成功檢測到圖案則返回True。這些角點會按特定順序排列(從左到右,從上到下)。
注意:此函數可能無法在所有圖像中找到目標圖案。因此,較好的做法是編寫代碼啟動攝像頭并逐幀檢測目標圖案。一旦檢測到圖案,就計算角點坐標并存入列表。同時,在讀取下一幀前設置適當間隔,以便調整棋盤方向。重復此過程直至獲得足夠數量的有效圖案。例如本文提供的14張樣本圖像中,我們也不確定有多少是有效的,因此需要全部讀取并篩選出有效圖像。
除了棋盤,我們也可以使用圓形網格。此時需改用 cv.findCirclesGrid() 函數來檢測圖案。使用圓形網格進行相機校準時,所需圖像數量更少。
檢測到角點后,可通過 cv.cornerSubPix() 提高其精度。還可以用 cv.drawChessboardCorners() 可視化圖案。以下代碼包含了上述所有步驟:
import numpy as np
import cv2 as cv
import glob# termination criteria
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001)# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)# Arrays to store object points and image points from all the images.
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.images = glob.glob('*.jpg')for fname in images:img = cv.imread(fname)gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)# Find the chess board cornersret, corners = cv.findChessboardCorners(gray, (7,6), None)# If found, add object points, image points (after refining them)if ret == True:objpoints.append(objp)corners2 = cv.cornerSubPix(gray,corners, (11,11), (-1,-1), criteria)imgpoints.append(corners2)# Draw and display the cornerscv.drawChessboardCorners(img, (7,6), corners2, ret)cv.imshow('img', img)cv.waitKey(500)cv.destroyAllWindows()
一張繪有圖案的圖片如下所示:

校準
現在我們已經獲得了物體點和圖像點,可以進行校準了。我們可以使用函數 cv.calibrateCamera(),該函數會返回相機矩陣、畸變系數、旋轉和平移向量等參數。
ret, mtx, dist, rvecs, tvecs = cv.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
去畸變
現在我們可以對圖像進行去畸變處理。OpenCV提供了兩種方法來實現這一功能。但首先,我們可以基于自由縮放參數使用**cv.getOptimalNewCameraMatrix()**來優化相機矩陣。如果縮放參數alpha=0,函數會返回去除最多無用像素的去畸變圖像,甚至可能裁切掉圖像角落的部分像素。若alpha=1,則保留所有像素并在圖像邊緣添加黑色區域。該函數還會返回一個圖像ROI區域,可用于裁剪最終結果。
這里我們以新圖像為例(本章第一個圖像left12.jpg)
img = cv.imread('left12.jpg')
h, w = img.shape[:2]
newcameramtx, roi = cv.getOptimalNewCameraMatrix(mtx, dist, (w,h), 1, (w,h))
1、使用 cv.undistort()
這是最簡單的方法。只需調用該函數,并使用之前獲取的ROI對結果進行裁剪。
# undistort
dst = cv.undistort(img, mtx, dist, None, newcameramtx)# crop the image
x, y, w, h = roi
dst = dst[y:y+h, x:x+w]
cv.imwrite('calibresult.png', dst)
2、使用重映射方法
這種方式稍復雜一些。首先需要找到一個從畸變圖像到無畸變圖像的映射函數,然后使用remap函數進行處理。
# undistort
mapx, mapy = cv.initUndistortRectifyMap(mtx, dist, None, newcameramtx, (w,h), 5)
dst = cv.remap(img, mapx, mapy, cv.INTER_LINEAR)# crop the image
x, y, w, h = roi
dst = dst[y:y+h, x:x+w]
cv.imwrite('calibresult.png', dst)
不過,這兩種方法得出的結果相同。查看下方結果:

從結果中可以看到所有邊緣都保持筆直。
現在,你可以使用NumPy的寫入函數(如np.savez、np.savetxt等)存儲相機矩陣和畸變系數,以便后續使用。
重投影誤差
重投影誤差能有效評估所找到參數的精確程度。該誤差值越接近零,表示我們獲得的參數越準確。在已知內參矩陣、畸變系數、旋轉矩陣和平移矩陣的情況下,我們需要先使用 cv.projectPoints() 將物體點轉換為圖像點。然后,可以計算通過該變換得到的點與角點檢測算法找到的點之間的絕對范數。要計算平均誤差,需對所有標定圖像計算得到的誤差取算術平均值。
mean_error = 0
for i in range(len(objpoints)):imgpoints2, _ = cv.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)error = cv.norm(imgpoints[i], imgpoints2, cv.NORM_L2)/len(imgpoints2)mean_error += errorprint( "total error: {}".format(mean_error/len(objpoints)) )
練習
1、嘗試使用圓形網格進行相機標定。
本文檔由 doxygen 1.12.0 生成于 2025年4月30日 星期三 23:08:42,針對 OpenCV 項目
姿態估計
https://docs.opencv.org/4.x/d7/d53/tutorial_py_pose.html
目標
在本節中,
- 我們將學習利用 calib3d 模塊在圖像中創建一些 3D 效果。
基礎
這部分內容會比較簡短。在上次關于相機校準的課程中,你已經獲取了相機矩陣、畸變系數等參數。給定一個標定板圖像,我們可以利用這些信息來計算其姿態(即物體在空間中的位置和方向),例如物體的旋轉角度、位移情況等。對于平面物體,我們可以假設Z=0,這樣問題就轉化為:相機在空間中如何擺放才能觀測到我們的標定板圖像。因此,如果我們知道物體在空間中的位置,就可以繪制一些2D圖形來模擬3D效果。下面我們來看看具體實現方法。
我們的目標是:在棋盤格的第一個角點繪制3D坐標軸(X、Y、Z軸),其中X軸用藍色表示,Y軸用綠色表示,Z軸用紅色表示。最終效果中,Z軸應該看起來垂直于棋盤格平面。
首先,我們需要從之前的校準結果中加載相機矩陣和畸變系數。
import numpy as np
import cv2 as cv
import glob# Load previously saved data
with np.load('B.npz') as X:mtx, dist, _, _ = [X[i] for i in ('mtx','dist','rvecs','tvecs')]
現在我們來創建一個函數 draw,它接收棋盤角點(通過 cv.findChessboardCorners() 獲取)和 坐標軸點 作為參數,用于繪制3D坐標軸。
def draw(img, corners, imgpts):corner = tuple(corners[0].ravel().astype("int32"))imgpts = imgpts.astype("int32")img = cv.line(img, corner, tuple(imgpts[0].ravel()), (255,0,0), 5)img = cv.line(img, corner, tuple(imgpts[1].ravel()), (0,255,0), 5)img = cv.line(img, corner, tuple(imgpts[2].ravel()), (0,0,255), 5)return img
與之前的情況類似,我們創建終止條件、對象點(棋盤角點的3D坐標)和軸點。軸點是用于繪制坐標軸的3D空間點。我們繪制長度為3的坐標軸(單位將基于棋盤方格尺寸,因為校準時使用了該尺寸)。因此,X軸從(0,0,0)繪制到(3,0,0),Y軸同理。Z軸則從(0,0,0)繪制到(0,0,-3),負號表示該軸向相機方向延伸。
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)axis = np.float32([[3,0,0], [0,3,0], [0,0,-3]]).reshape(-1,3)
按照慣例,我們首先加載每張圖像。搜索7x6的網格,如果找到,就用亞角點像素進行細化。接著,為了計算旋轉和平移矩陣,我們調用函數 cv.solvePnPRansac()。得到這些變換矩陣后,我們將其用于將坐標軸點投影到圖像平面。簡而言之,就是找到3D空間中(3,0,0)、(0,3,0)、(0,0,3)各點在圖像平面對應的位置。獲取這些點后,通過generateImage()函數從第一個角點向這些點繪制連線。搞定!
for fname in glob.glob('left*.jpg'):img = cv.imread(fname)gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)ret, corners = cv.findChessboardCorners(gray, (7,6),None)if ret == True:corners2 = cv.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)# Find the rotation and translation vectors.ret,rvecs, tvecs = cv.solvePnP(objp, corners2, mtx, dist)# project 3D points to image planeimgpts, jac = cv.projectPoints(axis, rvecs, tvecs, mtx, dist)img = draw(img,corners2,imgpts)cv.imshow('img',img)k = cv.waitKey(0) & 0xFFif k == ord('s'):cv.imwrite(fname[:6]+'.png', img)cv.destroyAllWindows()
以下是部分結果展示。請注意,每個坐標軸的長度為3個方格:

渲染立方體
如需繪制立方體,請按以下方式修改 generateImage() 函數及坐標點。
修改后的 generateImage() 函數:
def draw(img, corners, imgpts):imgpts = np.int32(imgpts).reshape(-1,2)# draw ground floor in greenimg = cv.drawContours(img, [imgpts[:4]],-1,(0,255,0),-3)# draw pillars in blue colorfor i,j in zip(range(4),range(4,8)):img = cv.line(img, tuple(imgpts[i]), tuple(imgpts[j]),(255),3)# draw top layer in red colorimg = cv.drawContours(img, [imgpts[4:]],-1,(0,0,255),3)return img
修改后的坐標軸點。它們是三維空間中立方體的8個角點:
axis = np.float32([[0,0,0], [0,3,0], [3,3,0], [3,0,0],[0,0,-3],[0,3,-3],[3,3,-3],[3,0,-3] ])
看看下面的結果:

如果你對圖形學、增強現實等領域感興趣,可以使用OpenGL來渲染更復雜的圖形。
生成于2025年4月30日星期三 23:08:42,由doxygen 1.12.0為OpenCV生成
極線幾何
https://docs.opencv.org/4.x/da/de9/tutorial_py_epipolar_geometry.html
目標
在本節中,
- 我們將學習多視圖幾何的基礎知識
- 我們將了解什么是極點(epipole)、極線(epipolar lines)、極線約束(epipolar constraint)等概念
基礎概念
當我們使用針孔相機拍攝圖像時,會丟失一個重要信息——圖像的深度。由于這是從3D到2D的轉換,我們無法知道圖像中每個點距離相機有多遠。因此,能否利用這些相機獲取深度信息成為一個關鍵問題。解決方案就是使用多個相機。人類視覺系統采用類似原理,通過雙目(兩只眼睛)實現立體視覺。下面我們來看看OpenCV在這方面提供的功能。
(Gary Bradsky所著的《Learning OpenCV》包含該領域的豐富信息。)
在探討深度圖像之前,我們先了解多視圖幾何中的一些基礎概念。本節將重點介紹極線幾何。觀察下圖展示的雙相機拍攝同一場景的基本配置:
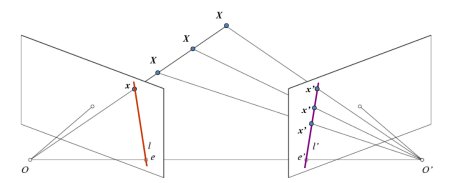
如果僅使用左相機,我們無法確定圖像中點\(x\)對應的3D空間點,因為直線\(OX\)上的所有點在成像平面上都會投影到同一位置。但若同時考慮右相機圖像,此時直線\(OX\)上的不同點會在右平面投影為不同位置(\(x’\))。通過這兩幅圖像,我們就能三角測量出正確的3D點坐標,這就是核心原理。
在右平面上,\(OX\)直線上不同點的投影會形成一條直線(\(l’\)),我們稱之為點\(x\)對應的極線。這意味著要在右圖像中尋找點\(x\),只需沿這條極線搜索即可(設想一下:要在另一幅圖像中尋找匹配點,無需搜索整個圖像,只需沿極線搜索即可。這種方式能提高性能和精度)。這個原理稱為極線約束。同理,所有點在另一幅圖像中都有對應的極線。平面\(XOO’\)被稱為極平面。
\(O\)和\(O’\)分別代表兩個相機的光心。從圖示配置可以看出,右相機\(O’\)的投影會出現在左圖像的\(e\)點處,這個點稱為極點。極點是連接兩個相機光心的直線與成像平面的交點。同理,\(e’\)是左相機的極點。某些情況下,極點可能位于圖像外部(即一個相機無法看到另一個相機)。
所有極線都會通過其對應的極點。因此要確定極點位置,可以通過多條極線的交點來實現。
本節重點在于尋找極線和極點。但在此之前,我們還需要兩個關鍵要素:基礎矩陣(F)和本質矩陣(E)。本質矩陣包含平移和旋轉信息,用于描述第二個相機相對于第一個相機在全局坐標系中的位置。見下圖(圖片來源:Gary Bradsky《Learning OpenCV》):
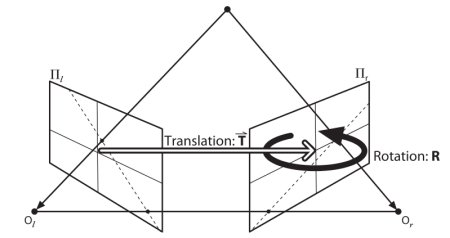
但實際測量通常采用像素坐標,對吧?基礎矩陣不僅包含與本質矩陣相同的信息,還包含兩個相機的內參信息,因此可以在像素坐標系中建立兩個相機的關聯(如果使用校正后的圖像并通過焦距歸一化點坐標,則\(F=E\))。簡而言之,基礎矩陣F能將一個圖像中的點映射到另一個圖像中的極線上。該矩陣通過兩幅圖像的匹配點計算得出,使用8點算法時至少需要8對匹配點。建議使用更多匹配點并結合RANSAC算法以獲得更穩健的結果。
代碼
首先,我們需要在兩幅圖像之間找到盡可能多的匹配點,以計算基礎矩陣。為此,我們使用基于FLANN匹配器的SIFT描述符,并采用比率測試方法。
import numpy as np
import cv2 as cv
from matplotlib import pyplot as pltimg1 = cv.imread('myleft.jpg', cv.IMREAD_GRAYSCALE) #queryimage # left image
img2 = cv.imread('myright.jpg', cv.IMREAD_GRAYSCALE) #trainimage # right imagesift = cv.SIFT_create()# find the keypoints and descriptors with SIFT
kp1, des1 = sift.detectAndCompute(img1,None)
kp2, des2 = sift.detectAndCompute(img2,None)# FLANN parameters
FLANN_INDEX_KDTREE = 1
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
search_params = dict(checks=50)flann = cv.FlannBasedMatcher(index_params,search_params)
matches = flann.knnMatch(des1,des2,k=2)pts1 = []
pts2 = []# ratio test as per Lowe's paper
for i,(m,n) in enumerate(matches):if m.distance < 0.8*n.distance:pts2.append(kp2[m.trainIdx].pt)pts1.append(kp1[m.queryIdx].pt)
現在我們得到了兩幅圖像的最佳匹配點列表。接下來計算基礎矩陣(Fundamental Matrix)。
def drawlines(img1,img2,lines,pts1,pts2):''' img1 - image on which we draw the epilines for the points in img2lines - corresponding epilines '''r,c = img1.shapeimg1 = cv.cvtColor(img1,cv.COLOR_GRAY2BGR)img2 = cv.cvtColor(img2,cv.COLOR_GRAY2BGR)for r,pt1,pt2 in zip(lines,pts1,pts2):color = tuple(np.random.randint(0,255,3).tolist())x0,y0 = map(int, [0, -r[2]/r[1] ])x1,y1 = map(int, [c, -(r[2]+r[0]*c)/r[1] ])img1 = cv.line(img1, (x0,y0), (x1,y1), color,1)img1 = cv.circle(img1,tuple(pt1),5,color,-1)img2 = cv.circle(img2,tuple(pt2),5,color,-1)return img1,img2
接下來我們尋找極線。在第一幅圖像中點的對應極線會被繪制在第二幅圖像上,因此這里正確指定圖像非常重要。我們會得到一個線條數組,為此我們定義一個新函數來在圖像上繪制這些線條。
def drawlines(img1,img2,lines,pts1,pts2):''' img1 - image on which we draw the epilines for the points in img2lines - corresponding epilines '''r,c = img1.shapeimg1 = cv.cvtColor(img1,cv.COLOR_GRAY2BGR)img2 = cv.cvtColor(img2,cv.COLOR_GRAY2BGR)for r,pt1,pt2 in zip(lines,pts1,pts2):color = tuple(np.random.randint(0,255,3).tolist())x0,y0 = map(int, [0, -r[2]/r[1] ])x1,y1 = map(int, [c, -(r[2]+r[0]*c)/r[1] ])img1 = cv.line(img1, (x0,y0), (x1,y1), color,1)img1 = cv.circle(img1,tuple(pt1),5,color,-1)img2 = cv.circle(img2,tuple(pt2),5,color,-1)return img1,img2
現在我們在兩張圖像中找到并繪制對極線。
# Find epilines corresponding to points in right image (second image) and
# drawing its lines on left image
lines1 = cv.computeCorrespondEpilines(pts2.reshape(-1,1,2), 2,F)
lines1 = lines1.reshape(-1,3)
img5,img6 = drawlines(img1,img2,lines1,pts1,pts2)# Find epilines corresponding to points in left image (first image) and
# drawing its lines on right image
lines2 = cv.computeCorrespondEpilines(pts1.reshape(-1,1,2), 1,F)
lines2 = lines2.reshape(-1,3)
img3,img4 = drawlines(img2,img1,lines2,pts2,pts1)plt.subplot(121),plt.imshow(img5)
plt.subplot(122),plt.imshow(img3)
plt.show()
以下是我們的處理結果:

從左側圖像可以看出,所有極線都在圖像右側外的一個點匯聚。這個交匯點就是極點。
為了獲得更好的效果,建議使用高分辨率且包含大量非共面點的圖像。
練習
1、一個重要議題是相機的前向運動。此時在兩幅圖像中極點會出現在相同位置,而極線會從固定點發散。參見此討論。
2、基礎矩陣估計對匹配質量、異常值等非常敏感。當所有選定匹配點都位于同一平面時,情況會變得更糟。查看此討論。
生成于 2025年4月30日 星期三 23:08:42,使用 doxygen 1.12.0 為 OpenCV 生成
從立體圖像生成深度圖
https://docs.opencv.org/4.x/dd/d53/tutorial_py_depthmap.html
目標
在本節課程中,
- 我們將學習如何從立體圖像創建深度圖。
基礎概念
在上節課中,我們學習了極線約束等基礎概念及相關術語。我們還了解到,如果擁有同一場景的兩幅圖像,就能以直觀的方式從中獲取深度信息。下圖及簡單數學公式將驗證這一原理(圖片來源):
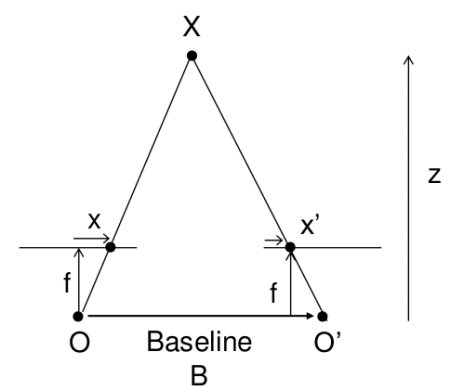
上圖展示了一組相似三角形。通過建立等價方程可得到以下結果:
\[視差 = x - x’ = \frac{Bf}{Z}\]
其中,\(x\)和\(x’\)分別表示三維場景點在圖像平面上的對應點與各自相機中心之間的距離。\(B\)代表雙相機間距(已知參數),\(f\)為相機焦距(已知參數)。簡而言之,該公式表明場景點的深度與對應圖像點及其相機中心距離差成反比。基于此原理,我們可以計算圖像中所有像素的深度值。
該過程需要在兩幅圖像間尋找對應匹配點。此前我們已經了解極線約束如何加速并提升該操作的準確性。找到匹配點后即可計算視差。接下來我們將學習如何通過OpenCV實現這一過程。
代碼
以下代碼片段展示了一個創建視差圖的簡單流程。
import numpy as np
import cv2 as cv
from matplotlib import pyplot as pltimgL = cv.imread('tsukuba_l.png', cv.IMREAD_GRAYSCALE)
imgR = cv.imread('tsukuba_r.png', cv.IMREAD_GRAYSCALE)stereo = cv.StereoBM.create(numDisparities=16, blockSize=15)
disparity = stereo.compute(imgL,imgR)
plt.imshow(disparity,'gray')
plt.show()
下圖展示了原始圖像(左)及其視差圖(右)。可以看到結果中存在大量噪聲污染。通過調整 numDisparities 和 blockSize 的數值,可以獲得更好的效果。

熟悉 StereoBM 后,您需要微調以下參數以獲得更平滑的結果:
- texture_threshold:過濾掉紋理不足、無法進行可靠匹配的區域
- Speckle range 和 size:基于塊的匹配器常在物體邊界處產生"斑點",此時匹配窗口會同時捕捉前景和背景。該場景中,匹配器還會在桌面的投影紋理上找到小的偽匹配。通過
speckle_size(視為斑點的最大像素數)和speckle_range(判定為同一斑點的視差值相近度)參數控制的斑點濾波器可消除這些偽影 - Number of disparities:滑動窗口的像素范圍。值越大可見深度范圍越廣,但計算量也越大
- min_disparity:從左側像素的x坐標開始搜索的偏移量
- uniqueness_ratio:后過濾步驟。若最佳匹配視差與搜索范圍內其他視差相比優勢不足,則過濾該像素。當紋理閾值和斑點過濾仍存在偽匹配時可調整此參數
- prefilter_size 和 prefilter_cap:預處理階段用于歸一化圖像亮度并增強紋理(為塊匹配做準備),通常無需調整
這些參數需在算法初始化后通過專用設置器配置,例如 setTextureThreshold、setSpeckleRange、setUniquenessRatio 等。詳見 cv::StereoBM 文檔。
附加資源
- ROS立體圖像處理維基頁面
練習
1、OpenCV示例中包含一個生成視差圖及其3D重建的案例。請查看OpenCV-Python示例中的stereo_match.py文件。
生成于2025年4月30日 星期三 23:08:42,由doxygen 1.12.0為OpenCV生成
2-=025-07-19(六)










)
 - 一個簡單web項目-實現鏈路跟蹤)



)



