?????????Hello大家好！很高興我們又見面啦！給生活添點passion，開始今天的編程之路！

我的博客：<但凡.

我的專欄：《編程之路》、《數據結構與算法之美》、《C++修煉之路》、《Linux修煉：終端之內 洞悉真理》

感謝你打開這篇博客！希望這篇博客能為你帶來幫助，也歡迎一起交流探討，共同成長。

? ? ? ? 拓撲排序其實是圖相關的內容，但是當時我忘了這一部分了，所以單獨拿一篇文章來補充上。

目錄

1、拓撲排序概述

2、拓撲排序的實現?

基于鄰接表的實現

Kahn算法實現（基于入度）

關鍵注意事項

3、應用場景擴展

---

?

1、拓撲排序概述

????????拓撲排序是對有向無環圖（DAG）的頂點進行線性排序，使得對于圖中的每一條有向邊 (u, v)，頂點 u 在排序中總是位于頂點 v 的前面。常用于任務調度、依賴解析等場景。

? ? ? ? 簡單來說，拓撲排序就是每次從入度為0的點開始，每次都走入度為0的點，直到遍歷完所有的頂點。拓撲排序只適用于有向無環圖，并且，拓撲排序的結果可能不唯一。

2、拓撲排序的實現?

基于鄰接表的實現

以下是使用鄰接表和深度優先搜索（DFS）的C++實現：

#include <iostream>
#include <vector>
#include <stack>
#include <list>
using namespace std;class Graph {int V; // 頂點數list<int>* adj; // 鄰接表void topologicalSortUtil(int v, bool visited[], stack<int>& Stack);public:Graph(int V);void addEdge(int v, int w);void topologicalSort();
};Graph::Graph(int V) {this->V = V;adj = new list<int>[V];
}void Graph::addEdge(int v, int w) {adj[v].push_back(w); // 添加邊v->w
}void Graph::topologicalSortUtil(int v, bool visited[], stack<int>& Stack) {visited[v] = true;for (auto i = adj[v].begin(); i != adj[v].end(); ++i)if (!visited[*i])topologicalSortUtil(*i, visited, Stack);Stack.push(v);
}void Graph::topologicalSort() {stack<int> Stack;bool* visited = new bool[V];for (int i = 0; i < V; i++)visited[i] = false;for (int i = 0; i < V; i++)if (!visited[i])topologicalSortUtil(i, visited, Stack);while (!Stack.empty()) {cout << Stack.top() << " ";Stack.pop();}
}int main() {Graph g(6);g.addEdge(5, 2);g.addEdge(5, 0);g.addEdge(4, 0);g.addEdge(4, 1);g.addEdge(2, 3);g.addEdge(3, 1);cout << "拓撲排序結果: ";g.topologicalSort();return 0;
}

? ? ? ? 我們來分析以下上面的算法，其實關于dfs，還是那句“一條路走到黑”來概括更為合適。我們在只要遍歷到入度為0的點，就以這個點為起點開始dfs，在dfs過程中遇到的所有點都先加入棧，最后，再依次彈出棧。光說不好理解，我們看圖來理解一下：

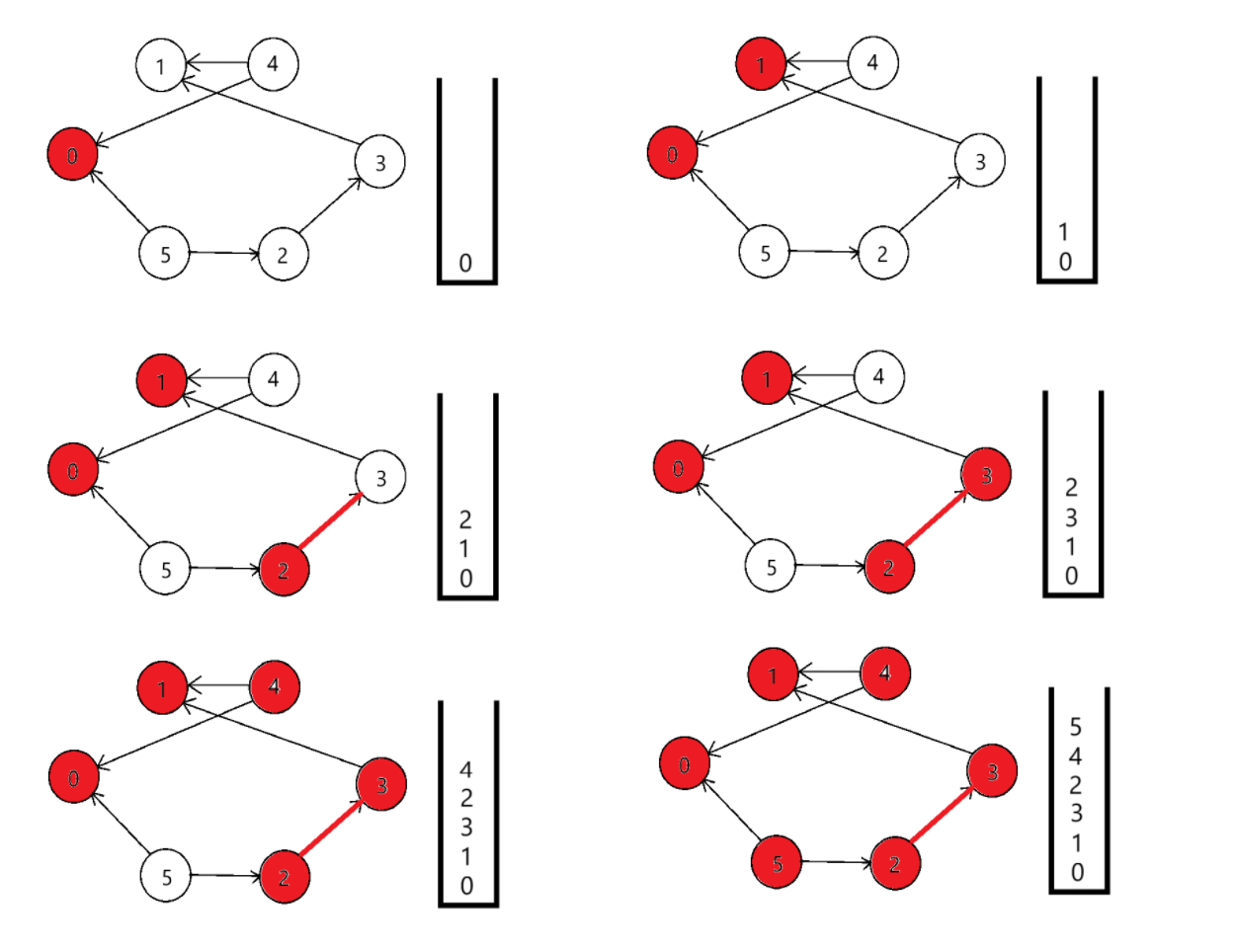
? ? ? ? 最后再依次出棧，就是拓撲排序。?

Kahn算法實現（基于入度）

? ? ? ? 其實一般提到拓撲排序，都是基于Kahn算法實現的。Kahn算法通過維護入度表實現拓撲排序，步驟如下：

#include <iostream>
#include <vector>
#include <queue>
using namespace std;vector<int> topologicalSort(int V, vector<vector<int>>& adj) {vector<int> inDegree(V, 0);queue<int> q;vector<int> result;// 計算每個頂點的入度for (int u = 0; u < V; u++)for (int v : adj[u])inDegree[v]++;// 入度為0的頂點入隊for (int i = 0; i < V; i++)if (inDegree[i] == 0) q.push(i);while (!q.empty()) {int u = q.front();q.pop();result.push_back(u);for (int v : adj[u])if (--inDegree[v] == 0)q.push(v);}if (result.size() != V) {cout << "圖中存在環！" << endl;return {};}return result;
}int main() {int V = 6;vector<vector<int>> adj(V);adj[5] = {2, 0};adj[4] = {0, 1};adj[2] = {3};adj[3] = {1};vector<int> sorted = topologicalSort(V, adj);for (int v : sorted) cout << v << " ";return 0;
}

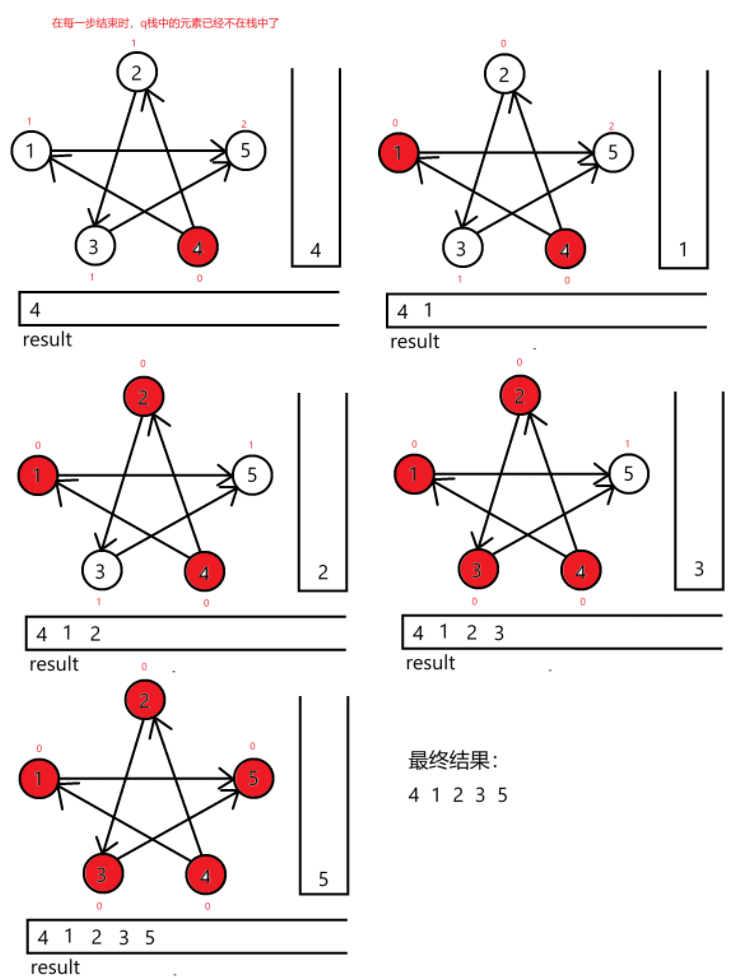
? ? ? ? 我們還是根據圖來理解一下：

?

關鍵注意事項

• 兩種方法時間復雜度均為 O(V+E)，其中V為頂點數，E為邊數
• DFS實現的結果是逆序的，需要通過棧反轉輸出
• Kahn算法可以直接檢測圖中是否存在環（當結果集大小不等于頂點數時）

3、應用場景擴展

拓撲排序可應用于：

• 編譯器中的指令調度
• 軟件包依賴管理（如apt-get/yum）
• 課程選修順序規劃
• 任務調度系統

????????兩種實現方式各有優劣：DFS代碼簡潔但需要額外空間存儲棧；Kahn算法更直觀且能直接檢測環，但需要維護入度表。根據具體場景選擇合適實現。但是我個人認為還是Kahn算法更好想一些。

? ? ? ? 好了，今天的內容就分享到這，我們下期再見！?

?