TASK01【datawhale組隊學習】地瓜機器人具身智能概述

https://github.com/datawhalechina/ai-hardware-robotics
參考資料地址

具身智能（Embodied AI）具身智能 = 智能的大腦 + 行動的身體。
比例（Proportional）、積分（Integral）、微分（Derivative）

具身智能，指的是能夠通過 物理身體（如機器人、自動駕駛汽車等）在真實世界中進行感知、交互和學習的智能系統。它強調智能體必須擁有一個“身體”（Body），并通過這個身體與環境互動，從而獲得對世界更深層次、更符合物理規律的理解。

具身智能概述

重要三要素身體、大腦、環境

身體（Body）：智能體的物理形態，包括各種傳感器（如攝像頭、激光雷達、觸覺傳感器）用于感知，以及執行器（如電機、機械臂、輪子）用于行動。
大腦（Brain）：即智能算法的核心，負責處理來自傳感器的數據，進行思考、決策，并向執行器發出指令。這通常涉及到深度學習、強化學習、大語言模型等前沿AI技術。
環境（Environment）：智能體所處的物理世界。它是智能體學習和實踐的舞臺，充滿著不確定性、動態變化和復雜的物理規律。

發展的脈絡

第一階段（20 世紀中葉 - 20 世紀末）：

理論構想的提出與早期實體機器人的嘗試。控制論創始人等率先提出機器與環境交互的理念，為具身智能奠定理論基礎。
標志性成果是世界首臺移動機器人 Shakey 的誕生，它首次實現了感知、推理和行動的系統整合，雖行動遲緩，但開啟了具身智能從概念到實體的探索。
第二階段（21 世紀初 - 2020 年）：
深度學習技術推動機器人感知與學習能力的躍升。算力提升讓計算機視覺技術成熟，賦予機器人更敏銳的 “視覺”；強化學習使機器人能通過試錯自主學習復雜技能。
突出成果體現在運動控制與平衡能力的飛躍，以波士頓動力為代表，其大狗機器人、Atlas 人形機器人等展現了具身智能在動態運動上的驚人水平。
第三階段（2021 年 - 至今）：
大語言模型（LLM）成為具身智能的 “大腦”，帶來范式轉移。LLM 的通用理解和推理能力，讓機器人能理解復雜指令并分解為具體行動步驟。
代表性突破包括谷歌 RT-2 模型實現 “視覺 - 語言 - 行動” 端到端控制、特斯拉 Optimus 依托自動駕駛技術打造通用人形機器人、Figure AI 與 OpenAI 合作整合對話推理能力，推動具身智能向通用化邁進。

面臨的挑戰

核心挑戰：
“Sim-to-Real”的鴻溝：在模擬器中訓練好的模型，轉移到現實世界時往往會“水土不服”，因為現實世界充滿了模擬器無法窮盡的細節和意外。
泛化能力：如何讓機器人在面對從未見過的物體和環境時，依然能做出正確的決策和行動，這是實現“通用”的關鍵。
數據稀缺：與互聯網上取之不盡的文本和圖片數據不同，高質量的機器人交互數據既昂貴又難以獲取。
安全性與倫理：一個擁有強大物理能力的AI系統，如何確保其行為的安全、可控和符合人類倫理，是一個必須嚴肅對待的問題。

PID_control

首先學習 PID控制算法掌握基礎控制原理
了解不同控制參數對系統響應的影響
嘗試調整PID參數以獲得最佳控制效果
進階學習高級控制算法（待更新）

PID控制算法是工業自動化中最常用的控制算法之一。
什么是PID算法：PID通過計算當前輸出與期望輸出之間的誤差，并根據該誤差的比例（P）、積分（I）和微分（D）來調整控制輸入，從而實現對系統的精確控制。

工作原理

PID控制器通過以下三個基本組件來計算控制輸入：

比例（P）：【快速相應誤差】直接對誤差進行比例放大，可以迅速減少誤差，但可能導致系統不穩定。
- 舉例：如果當前溫度 20℃（誤差 5℃），P 環節會讓空調加大制熱功率（比如開 50% 功率）；如果誤差減小到 1℃，功率就降低到 10%。
- 特點：能快速縮小誤差，但單獨使用時，可能因為 “慣性” 導致系統在目標值附近波動（比如溫度超過 25℃后，空調才開始減小功率），難以完全消除誤差（稱為 “穩態誤差”）。
積分（I）：【消除累積誤差】對誤差進行積分，可以消除系統的靜態誤差，但可能導致系統響應變慢。根據誤差的 “累積時間” 調整 —— 如果誤差長期存在（比如溫度一直差 1℃），積分環節會逐漸加大控制力度，直到誤差徹底消除。
- 舉例：如果溫度穩定在 24℃（誤差 1℃），P 環節可能認為誤差小而停止調整，但 I 環節會累計這個 1℃的誤差（比如累計 10 分鐘后），驅動空調略微加大功率，最終讓溫度達到 25℃。
- 特點：解決 P 環節的 “穩態誤差”，但響應較慢，單獨使用可能導致系統超調（比如溫度超過 25℃后還在加熱）。
微分（D）：【預測誤差變化趨勢】對誤差的導數進行預測，可以預測誤差的變化趨勢，從而提前進行調整，提高系統的響應速度和穩定性。
- 舉例：如果溫度從 20℃快速升到 24℃（1 分鐘內升了 4℃），D 環節會預測 “可能很快超過 25℃”，提前讓空調減小制熱功率，避免溫度過高。
- 作用：根據誤差的 “變化速度” 調整 —— 如果誤差突然變大（或變小），D 環節會提前輸出反向控制信號，抑制系統的劇烈變化。

$e (t)$ 是當前誤差，即期望輸出與實際輸出之間的差值。

$K_p$ 是比例系數。
$K_i$ 是積分系數。
$K_d$ 是微分系數。

實現步驟

計算誤差：計算當前輸出與期望輸出之間的誤差。
- 比例項：根據比例系數和誤差計算比例項。
- 積分項：對誤差進行積分，并根據積分系數計算積分項。
- 微分項：計算誤差的導數，并根據微分系數計算微分項。
計算控制輸入：將比例項、積分項和微分項相加，得到控制輸入。
應用控制輸入：將控制輸入應用于被控系統。

整體公式：
$K_p \cdot e(t) + K_i \int_{0}^{t} e(\tau) \, d\tau + K_d \cdot \frac{de(t)}{dt}$

一般情況下，我們是通過波形圖的穩定以及響應來判定PID算法的效果的。
一般情況下，我們可以先設置一個較大的比例系數，然后逐漸減小比例系數，直到系統的響應變得平滑。
積分項的作用是消除系統的靜態誤差，但是積分項的引入會使系統的響應變慢。
微分項的作用是預測誤差的變化趨勢，從而提前進行調整，提高系統的響應速度和穩定性。

一般來說，位置PID控制算法可以穩定大部分的控制，但是根據不同的應用情景，也有不同的優化算法

積分分離PID
$K_P e(k) + \beta K_I \sum_{i=0}^{k} e(i) + K_D \left[ e(k) - e(k - 1) \right]$
變速積分的PID控制
$K_P e(k) + K_I \sum_{i=0}^{k} \alpha e(i) + K_D \left[ e(k) - e(k - 1) \right]$
不完全微分PID控制
$uD(k)=KD(1?α)[e(k)?e(k?1)]+αuD(k?1)u_D (k) = K_D (1 - \alpha) \left[ e(k) - e(k - 1) \right] + \alpha u_D (k - 1)$
示例代碼：

class PID:# pid的初始化賦值def __init__(self, Kp, Ki, Kd, setpoint=0, sample_time=0.01):self.Kp = Kpself.Ki = Kiself.Kd = Kdself.setpoint = setpointself.sample_time = sample_timeself.prev_error = 0self.integral = 0# pid的cal_processdef update(self, measured_value):error = self.setpoint - measured_value # 計算誤差self.integral += error * self.sample_time # 積分derivative = (error - self.prev_error) / self. sample_time # 微分output = self.Kp * error + self.Ki * self.integral + self.Kd * derivative # 計算控制輸入self.prev_error = error # 保存誤差return outputpid = PID(Kp=1.0, Ki=0.1, Kd=0.01, setpoint=100)
measured_value = 90  # 假設的當前測量值
control_input = pid.update(measured_value)print(f"Control Input: {control_input}")

c語言示例代碼

void pid_init(pid_type_def *pid,uint8_t mode,float max_output,float max_iout,const float PID[3])
{pid->mode=mode;pid->max_output=max_output;pid->max_ioutput=max_iout;pid->Dbuf[0]=pid->Dbuf[1]=pid->Dbuf[2];pid->error[0]=pid->error[1]=pid->error[2]=pid->pout=pid->iout=pid->dout=0.0f;
}float PID_calc(pid_type_def *pid,float ref,float set,float PID[3])
{pid->kp=PID[0];pid->ki=PID[1];pid->kd=PID[2];pid->error[2]=pid->error[1];pid->error[1]=pid->error[0];pid->set=set;pid->cur=ref;pid->error[0]=set-ref;if (pid->mode ==PID_POSITION){pid->pout=pid->kp*pid->error[0];pid->iout+=pid->ki*pid->error[0];pid->Dbuf[2]=pid->Dbuf[1];pid->Dbuf[1]=pid->Dbuf[0];pid->Dbuf[0]=pid->error[0]-pid->error[1];if (pid->iout>pid->max_ioutput){pid->iout=pid->max_ioutput;}else if (pid->iout<-pid->max_ioutput){pid->iout=-pid->max_ioutput;}if (pid->iout*pid->error[0]<0){pid->iout=0;}if (pid->cur>0.707*pid->set || pid->cur<0.707*pid->set){pid->dout=pid->kd*pid->Dbuf[0];}else{pid->dout=0;}pid->output=pid->pout+pid->iout+pid->dout;if (pid->output>pid->max_output){pid->output=pid->max_output;}}else if (pid->mode==PID_DELTA){pid->pout=pid->kp*(pid->error[0]-pid->error[1]);pid->iout=pid->ki*pid->error[0];if (pid->iout>pid->max_ioutput){pid->iout=pid->max_ioutput;}		else if (pid->iout<-pid->max_ioutput){pid->iout=-pid->max_ioutput;}if (pid->iout*pid->error[0]<0){pid->iout=0;}pid->Dbuf[2]=pid->Dbuf[1];pid->Dbuf[1]=pid->Dbuf[0];pid->Dbuf[0]=pid->error[0]-2.0f*pid->error[1]+pid->error[2];if (pid->cur>0.707*pid->set || pid->cur<0.707*pid->set){pid->dout=pid->kd*pid->Dbuf[0];}else{pid->dout=0;}pid->output+=pid->pout+pid->iout+pid->dout;if (pid->output>pid->max_output){pid->output=pid->max_output;}}return pid->output;
}

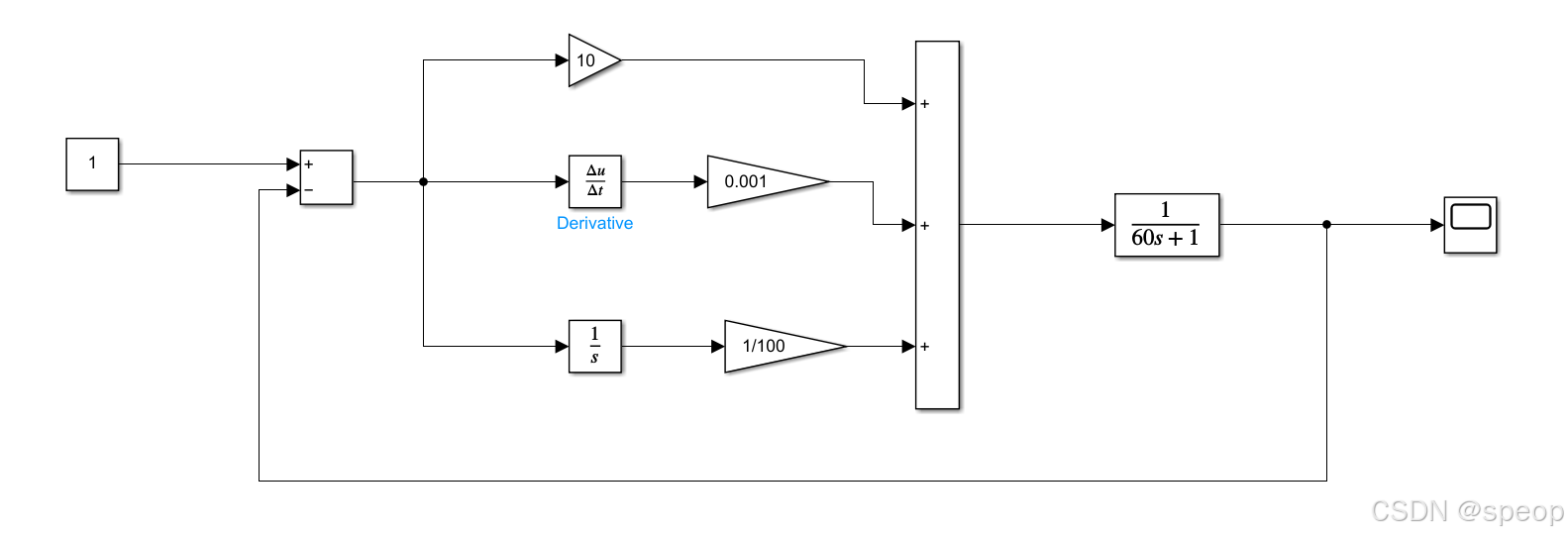
舉例分析 matlab-simulink

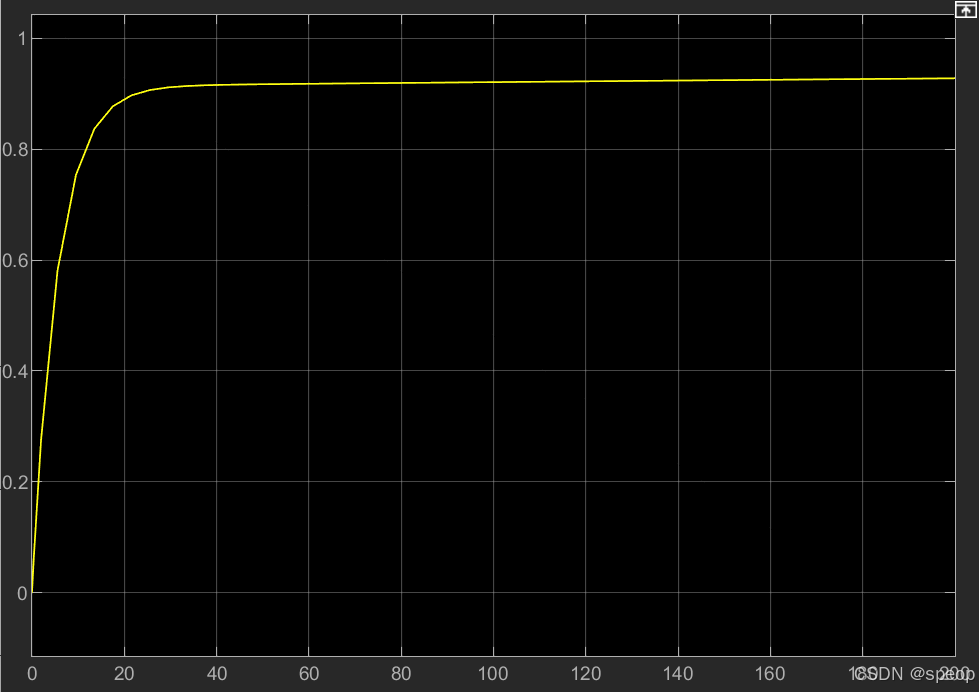
這是當P是10,I是0.001,D是0.01的時候matlab的simulink仿真圖以及他的效果圖,采樣周期T是200.
在這里插入圖片描述
說明存在穩態誤差，這個時候要增加i，使得不存在穩態誤差

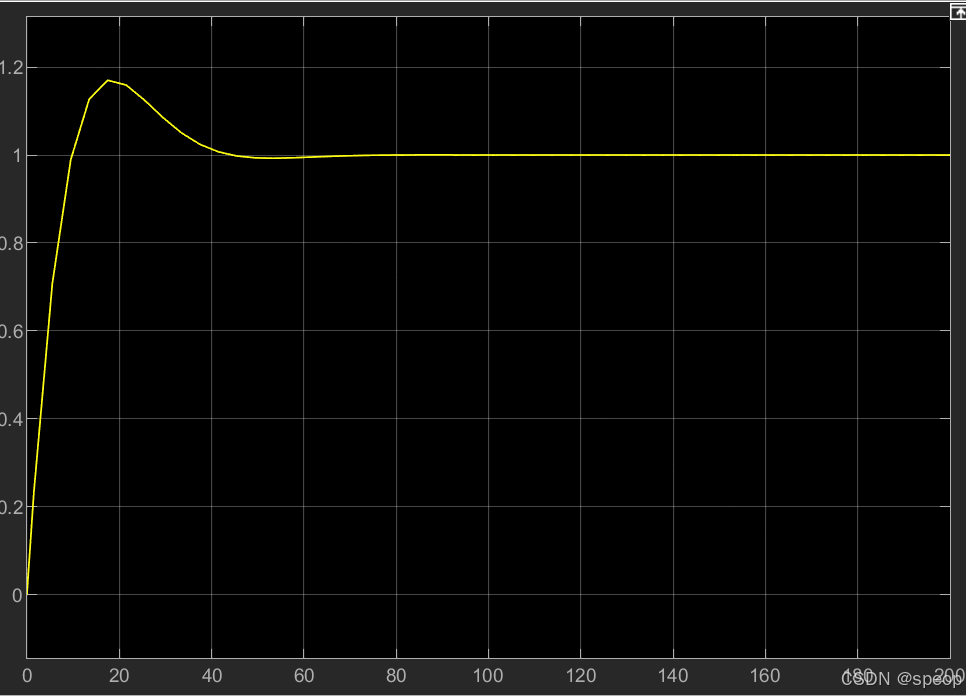
增加I的數值以后，發現超調，準備增加D

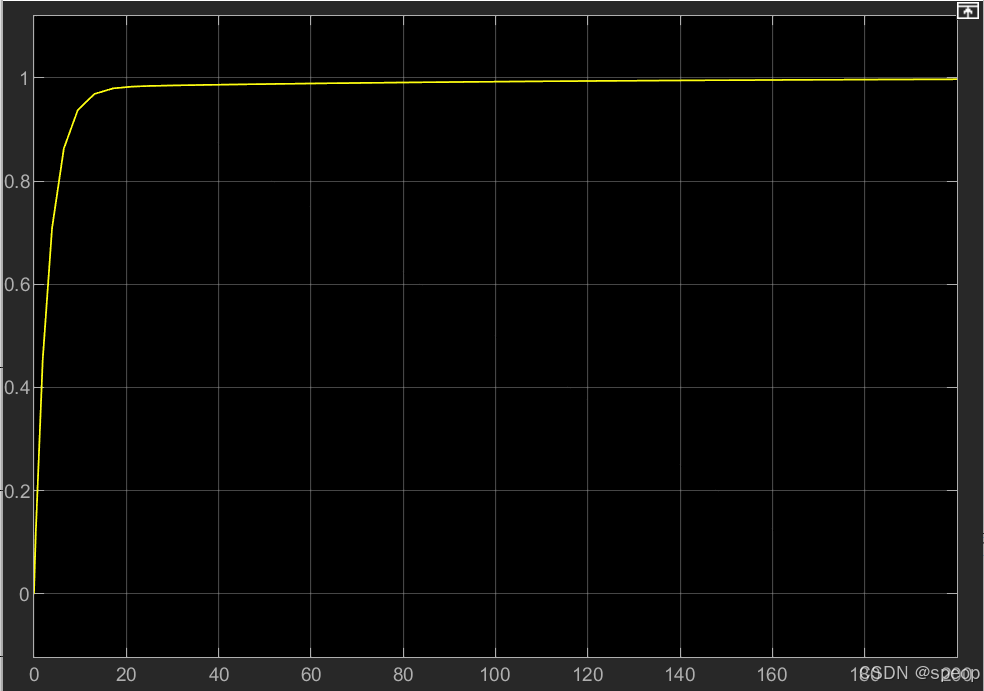
在這里插入圖片描述
最好的效果如下

優化以及其他情況的PID計算：

            參數整定找最佳， 從小到大順序查。先是比例后積分， 最后再把微分加。曲線振蕩很頻繁， 比例度盤要放大。曲線漂浮繞大彎， 比例度盤往小扳。曲線偏離回復慢， 積分時間往下降。曲線波動周期長， 積分時間再加長。曲線振蕩頻率快， 先把微分降下來。動差大來波動慢， 微分時間應加長。理想曲線兩個波， 前高后低四比一。一看二調多分析， 調節質量不會低。