統計學核心概念與現實應用精解（偏機器學習）

統計學聽起來似乎很復雜，但其實它的核心就是兩個概念：概率分布和期望。這兩個概念就像是我們日常生活中的決策助手。

概率分布描述了隨機事件各種可能結果出現的可能性大小。比如，擲骰子時每個點數出現的概率，這就是一個典型的概率分布。而期望則更像是一個長期的平均結果，它告訴我們如果多次重復某一行為，平均下來會得到什么結果。比如，長期玩骰子游戲，平均每次能贏多少錢。

在統計學中，所有的分析歸根結底都是圍繞這兩個概念展開的。就像物理學家用 E=mc2 這個公式統一了能量和質量的關系一樣，統計學家用概率分布和期望這兩個概念建立了一個理解不確定性的完整框架。

無論是簡單的拋硬幣、擲骰子，還是復雜的金融投資、風險評估，都可以用這兩個概念來建模和分析。概率分布幫助我們了解可能的結果及其可能性，而期望則幫助我們在不確定性中做出更合理的決策。

期望

1. 期望：加權平均的藝術

1.1 加權平均的深層含義

期望的核心是?用概率作為權重的加權平均，它與普通平均數的區別在于：

普通平均數：假設所有結果 “平等”（權重相同），如擲骰子點數的普通平均為? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? $(1+2+3+4+5+6)/6 = 3.5$ 。
期望（加權平均）：允許不同結果有不同權重（概率），適用于現實中 “可能性不均等” 的場景。案例：某股票未來一年漲 30% 的概率是 40%，跌 10% 的概率是 60%，其收益率期望為： $30\% \times 0.4 + (-10\%) \times 0.6 = 6\%$ ?這里漲跌幅的概率（40% 和 60%）就是權重，直接影響最終期望收益。

1.2?從頻率到概率的橋梁

期望的加權平均思想，本質上是將?統計頻率?抽象為?理論概率。

試驗層面：拋硬幣 1000 次，正面出現 502 次，頻率為 50.2%，接近理論概率 50%，此時期望近似為? $1 \times 0.502 + 0 \times 0.498 \approx 0.502$ 。
理論層面：直接用理論概率計算期望? $E(X) = 1 \times 0.5 + 0 \times 0.5 = 0.5$ ，無需依賴試驗次數。

2. 離散型期望：從骰子到投資的精準計算

2.1?公式細節與案例擴展

通用公式：

$E(X) = \sum_{i=1}^{n} x_i \cdot p_i \quad (\sum_{i=1}^{n} p_i = 1)$

?案例 1：抽獎游戲的 “陷阱” 某抽獎箱有 100 張獎券，其中 1 張一等獎（獎金 500 元），5 張二等獎（獎金 100 元），其余為謝謝參與。抽獎一次的期望收益為：

$E(X) = 500 \times \frac{1}{100} + 100 \times \frac{5}{100} + 0 \times \frac{94}{100} = 5 + 5 = 10 \text{yuan}$

若抽獎一次收費 20 元，則?期望凈收益為 - 10 元，長期參與必虧。

案例 2：保險定價邏輯 某保險公司推出重疾險，統計顯示某年齡段人群患重疾概率為 0.1%，重疾治療平均費用為 50 萬元。若保費定價為：?

$E(\text{Compensation Amount}) = 500000 \times 0.001 + 0 \times 0.999 = 500 \text{Yuan}$

則保費至少定為 500 元才能覆蓋期望成本（實際定價需疊加運營成本和利潤）。

3. 連續型期望：從身高分布到時間預測

3.1?積分背后的 “密度加權”

連續型變量的期望通過積分計算，核心是?概率密度函數（PDF）f (x)：

$E(X) = \int_{-\infty}^{+\infty} x \cdot f(x) \, dx$

$f(x) \, dx$ ?表示 x 附近微小間隔內的概率，類似離散型中的? $p(x)$ 。
積分本質是將連續區間分割為無數微小離散點，對每個點計算? $x \cdot p(x)$ ?后求和。

案例：公交車到站時間的期望 假設某公交站到站時間 X 服從均勻分布，范圍為 [0, 10] 分鐘（即 PDF 為?f(x) = 0.1，則平均等待時間期望為：

$E(X) = \int_{0}^{10} x \cdot 0.1 \, dx = 0.1 \times \frac{x^2}{2} \bigg|_{0}^{10} = 5 \text{mins}$

?均勻分布的期望正好是區間中點，符合直覺。

3.2?正態分布的期望：均值即中心

若 X 服從正態分布? $N(\mu, \sigma^2)$ ，其期望? $E(X) = \mu$ ，即正態曲線的對稱軸位置。案例：成年男性身高 X~N (175, 64)，則平均身高期望為 175cm，無需積分即可直接通過參數得出。

4. 期望的線性性質：復雜系統的簡化利器

4.1?線性性的 “反直覺” 與實用性

公式擴展： $E(aX + bY + c) = aE(X) + bE(Y) + c \quad (a, b, c \text{is a constant})$ ?反直覺點：即使 X 和 Y 存在強相關性（如身高 X 與體重 Y 正相關），線性性依然成立。 案例：投資組合的期望收益

股票 A 收益率 X~ 期望 10%，股票 B 收益率 Y~ 期望 8%，相關性 0.7。
投資組合 Z = 0.6X + 0.4Y，期望收益為：? $E(Z) = 0.6 \times 10\% + 0.4 \times 8\% = 9.2\%$ ?無需考慮 X 和 Y 的相關性，直接按權重計算期望，極大簡化組合分析。

4.2?線性性的數學證明（補充細節）

離散型嚴格證明：設二維離散變量 (X,Y) 的聯合概率為? $p(x_i, y_j)$ ，則：?

連續型同理：通過聯合密度函數? $f(x,y)$ ?積分，利用邊緣密度? $f(x) = \int f(x,y) dy$ ?化簡。

5. 期望的應用邊界：警惕 “平均” 背后的風險

5.1?期望相同，風險不同

案例：兩種投資方案：

方案 A：50% 概率賺 100 元，50% 概率虧 60 元，期望收益：? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? $E(A) = 100 \times 0.5 + (-60) \times 0.5 = 20 \text{Yuan}$
方案 B：100% 概率賺 20 元，期望收益： $E(B) = 20 \text{Yuan}$ ?雖然期望相同，但方案 A 存在虧損風險，需用方差等指標進一步衡量風險。

5.2 期望無法描述極端事件

案例：某地區洪水損失 X 的期望為 1000 元 / 年，但可能 50 年一遇的大洪水損失超百萬。僅看期望會低估極端風險，需結合分位數（如 95% 損失值）綜合評估。

6. 總結：期望的 “精準” 與 “局限”

維度	核心結論
定義本質	加權平均，用概率作為權重，融合所有可能結果的 “平均影響”。
公式差異	離散型用求和，連續型用積分，本質都是 “結果 × 權重” 的累加。
線性性質	無論變量是否相關，期望的線性組合恒成立，是統計推導和建模的基石。
應用提醒	期望僅反映平均趨勢，需結合方差、分布形態等評估風險，避免 “唯平均論”。

一句話點睛：期望是統計學的 “望遠鏡”，幫我們看清長期趨勢；但要避免成為 “顯微鏡”，忽略了趨勢背后的波動與極端可能。理解期望的價值與局限，才能在決策中真正實現 “用數據說話”。

概率分布：從 PMF 到 CDF

概率分布是統計學中的另一個核心概念，它描述了隨機變量取各種值的可能性。根據隨機變量的類型不同，概率分布的表示方法也有所不同。

離散型隨機變量：概率質量函數（PMF）

對于離散型隨機變量，例如擲骰子的結果，我們可以用概率質量函數（Probability Mass Function, PMF）來描述其分布。PMF 可以看作是一張表格，列出了每個可能值及其對應的概率。

舉例：擲一個公平的六面骰子，每個點數（1 到 6）出現的概率都是六分之一?。其 PMF 可以表示為：

PMF 的性質：

對于所有可能的 x，有 P(X=x)≥0。
所有可能值的概率之和為 1：

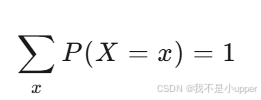
連續型隨機變量：概率密度函數（PDF）

對于連續型隨機變量，例如測量溫度或身高，我們用概率密度函數（Probability Density Function, PDF）來描述其分布。PDF 是一個非負函數，其圖像下方的總面積等于 1。PDF 在某一點的值可以大于 1，但整個曲線下的面積必須正好是 1。

舉例：一個正態分布（高斯分布）的 PDF 形式為：

其中，μ 是均值，σ 是標準差。PDF 的性質：

對于所有 x，有 f(x)≥0。
曲線下的總面積為 1：

累積分布函數（CDF）

累積分布函數（Cumulative Distribution Function, CDF）是另一個重要的概念，它表示隨機變量小于等于某個值的概率。CDF 是一個單調不減的函數，從 0 開始，最終上升到 1。

對于離散型隨機變量，CDF 是階梯狀的；對于連續型隨機變量，CDF 是一條平滑的曲線。

定義：

舉例：對于擲骰子的離散型隨機變量，其 CDF 在 x=1,2,3,4,5,6 處分別跳躍 61?，最終在 x=6 時達到 1。

對于連續型隨機變量，CDF 是 PDF 的積分：

PMF 和 PDF 的對應關系

PMF 和 PDF 是一一對應的，給定 PMF 可以計算出 CDF，反之亦然。對于離散型隨機變量，CDF 是 PMF 的累積和；對于連續型隨機變量，CDF 是 PDF 的積分。

總結來說，概率分布通過 PMF 或 PDF 描述了隨機變量的取值可能性，而 CDF 則提供了隨機變量小于等于某個值的累積概率。這些概念共同構成了統計學中描述和分析隨機現象的基礎。

聯合分布與邊緣分布

1. 聯合分布：多變量關系的 “全景地圖”

1.1 離散型聯合分布：用表格鎖定變量聯動

定義：對于兩個離散型隨機變量?X?和?Y，聯合分布通過?聯合概率質量函數（Joint PMF）?P(X=x, Y=y)?表示，所有可能的?(x, y) 組合概率之和為 1。

案例：擲兩枚硬幣的聯合分布 設?X?為第一枚硬幣正面次數（0 或 1），Y?為第二枚硬幣正面次數（0 或 1），假設硬幣獨立，則聯合分布表格為：

表格中的每個單元格是聯合概率，如? $P(X=1, Y=1) = \frac{1}{4}$ 。

最后一列和最后一行分別是?X?和?Y?的邊緣分布（下文詳述）。

1.2?連續型聯合分布：用曲面描述概率密度

定義：對于連續型隨機變量，聯合分布通過?聯合概率密度函數（Joint PDF）? $f_{X,Y}(x, y)$ ?描述，滿足：?

$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{X,Y}(x, y) \, dx \, dy = 1$

案例：二維正態分布 若身高?X?和體重?Y?服從二維正態分布，其聯合 PDF 為鐘形曲面，曲面高度反映?X, Y?組合的概率密度。例如， $f_{X,Y}(170, 65)$ ?的值越大，表示身高 170cm 且體重 65kg 的人越 “密集”。

2. 邊緣分布：從全局到局部的 “視角切換”

2.1?離散型邊緣分布：求和消元

計算邏輯：固定一個變量，對另一個變量的所有可能值求和，“消去” 該變量的影響。

X 的邊緣分布： $P(X=x) = \sum_{y} P(X=x, Y=y)$ ?（對每一行的聯合概率求和，得到?X?的單獨分布）
Y 的邊緣分布： $P(Y=y) = \sum_{x} P(X=x, Y=y)$ ?（對每一列的聯合概率求和，得到?Y?的單獨分布）

沿用擲硬幣案例：

X=0?的邊緣概率? $P(X=0) = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}$ ，與單枚硬幣正面概率一致。
邊緣分布僅描述單個變量，不涉及變量間的關系。

2.2?連續型邊緣分布：積分消元

計算邏輯：對聯合 PDF 中某一變量積分，消除其影響，得到另一變量的單獨密度函數。

X 的邊緣 PDF： $f_X(x) = \int_{-\infty}^{+\infty} f_{X,Y}(x, y) \, dy$ ?（固定?x，對?y?積分，得到?X?在?x?處的邊緣密度）
Y 的邊緣 PDF： $f_Y(y) = \int_{-\infty}^{+\infty} f_{X,Y}(x, y) \, dx$

案例：均勻分布的邊緣分布 設?X?和?Y?在單位正方形? $[0,1] \times [0,1]$ ?內服從均勻分布，聯合 PDF 為：

$f_{X,Y}(x, y) = \begin{cases} 1, & 0 \leq x \leq 1, 0 \leq y \leq 1 \\ 0, & \text{Other} \end{cases}$

X?的邊緣 PDF： $f_X(x) = \int_{0}^{1} 1 \, dy = 1 \quad (0 \leq x \leq 1)$ ?即?X?單獨服從?[0,1]?均勻分布，同理?Y?亦然。

3. 聯合分布 vs 邊緣分布：信息的得與失

3.1?從聯合到邊緣：信息的簡化

聯合分布包含?變量間的依賴關系（如身高與體重的正相關），而邊緣分布僅保留單個變量的信息，丟失了變量間的關聯。
案例：
- 聯合分布可判斷 “身高高的人是否更可能體重重”（通過觀察聯合概率的分布趨勢）。
- 邊緣分布只能回答 “身高的平均值是多少” 或 “體重的分布如何”，無法推斷兩者關系。

3.2?從邊緣到聯合：信息的缺失

核心結論：僅知邊緣分布，無法唯一確定聯合分布，除非變量獨立。反例：
- 設?X?和?Y?均為拋硬幣結果（0 或 1，邊緣分布均為?P=0.5）。
- 情況 1：X?和?Y?獨立，聯合分布如前所述（每個組合概率為 0.25）。
- 情況 2：X?和?Y?完全正相關(X=Y），聯合分布為：? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? $P(X=0, Y=0)=0.5, \quad P(X=1, Y=1)=0.5, \quad \text{The probability of other combinations is 0}$
- 兩種情況的邊緣分布相同，但聯合分布截然不同，說明邊緣分布不包含變量間依賴信息。

4. 獨立性：聯合分布的 “簡化開關”

4.1?獨立性的嚴格定義

隨機變量?X?和?Y?獨立，當且僅當：

離散型：對所有?x, y，有 $P(X=x, Y=y) = P(X=x) \cdot P(Y=y)$
連續型：對所有?x, y，有 $f_{X,Y}(x, y) = f_X(x) \cdot f_Y(y)$

4.2?獨立性的直觀理解

變量獨立意味著?一個變量的取值不影響另一個變量的概率。案例：

兩枚獨立骰子的點數?X?和?Y：? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? $P(X=3, Y=5) = P(X=3) \cdot P(Y=5) = \frac{1}{6} \times \frac{1}{6} = \frac{1}{36}$
非獨立案例：身高?X?與體重?Y?通常正相關，故? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? $P(Y>70 \, \text{kg} | X>180 \, \text{cm}) > P(Y>70 \, \text{kg})$ ，不滿足獨立條件。

4.3?獨立性的作用：簡化聯合分布計算

若變量獨立，復雜的聯合分布可分解為簡單的邊緣分布乘積，大幅降低計算復雜度。 應用場景：

風險建模：假設不同資產的收益率獨立，可快速計算投資組合的聯合風險。
機器學習：樸素貝葉斯算法假設特征獨立，將聯合概率分解為邊緣概率乘積，如：

統計學的兩大學派：頻率派與貝葉斯派

統計學界一直存在著兩大陣營的爭論，就像武俠小說里的兩大門派一樣，各有所長。這兩大學派分別是頻率派（Frequentist）和貝葉斯派（Bayesian）。它們在概率的定義和應用上有根本性的不同。

頻率派（Frequentist）

頻率派認為概率是事件在長期重復試驗中發生的頻率。例如，拋一枚硬幣，隨著拋擲次數的增加，正面朝上的比例會逐漸穩定在50%左右。這種概率是客觀存在的，不以人的意志為轉移。

主要特點：

客觀主義：概率是客觀存在的，與個人信念無關。
p值（p-value）：頻率派常用 p 值來衡量統計顯著性。p 值表示在原假設成立的情況下，觀測到當前數據或更極端數據的概率。如果 p 值小于某個顯著性水平（如 0.05），則拒絕原假設。
假設檢驗：頻率派常用假設檢驗來判斷某個假設是否成立。例如，在醫學試驗中判斷新藥是否有效。

局限性：

可重復性：頻率派的方法主要適用于可重復事件。對于唯一事件（如“明天是否降雨”），頻率派難以定義概率，因為無法進行多次重復觀測。

貝葉斯派（Bayesian）

貝葉斯派則認為概率是主觀信念的度量，反映了人們對事件發生的相信程度。概率計算中摻雜著人的主觀判斷。

主要特點：

主觀概率：概率是主觀信念的度量，不同的人可以根據不同的先驗信息得出不同的概率。
先驗概率（Prior Probability）：在觀察數據之前，對參數 θ 可能取值的概率分布的假設。例如，在相親前根據介紹人的描述對對方有個初步印象。
后驗概率（Posterior Probability）：在觀察數據后，對參數 θ 的概率分布的更新。例如，相親后根據實際相處情況調整對對方的印象。
貝葉斯公式：貝葉斯派的核心公式是：
P(θ∣D)∝P(D∣θ)?P(θ)
其中：
- P(θ∣D) 是后驗概率（Posterior），即在看到數據 D 后對參數 θ 的信念。
- P(D∣θ) 是似然函數（Likelihood），即在參數 θ 下觀測到數據 D 的概率。
- P(θ) 是先驗概率（Prior），即在看到數據 D 之前對參數 θ 的信念。

舉例：

天氣預報：貝葉斯派可以用來預測明天降雨的概率。假設根據歷史數據，明天降雨的概率是 30%。這個概率反映了氣象學家對降雨的相信程度，而不是基于多次重復觀測的結果。

兩大學派的現實交鋒

在實際應用中，兩大學派各有優勢和局限性。例如，在醫學試驗中：

頻率派：設計試驗時，通常會設定一個顯著性水平（如 0.05），通過假設檢驗來判斷新藥是否有效。頻率派強調“讓數據說話”，結果具有客觀性。
貝葉斯派：會先設定一個先驗概率（如“新藥有效的概率是 50%”），然后用試驗數據更新這個先驗概率，得到后驗概率。貝葉斯派直接回答了“新藥有效的概率是多少”這個問題，但其結果可能因先驗概率的不同而有所差異。

總結

頻率派和貝葉斯派在概率的定義和應用上有根本性的不同。頻率派強調概率的客觀性和長期頻率，適用于可重復事件；貝葉斯派則強調概率的主觀信念，適用于唯一事件和需要結合先驗信息的場景。在實際應用中，兩者的結合使用可以取長補短，更好地解決復雜問題。理解這兩大學派的觀點和方法，有助于我們在不確定性中做出更合理的決策。

似然函數：數據與參數的對話橋梁

在統計學的探索旅程中，似然函數猶如一座精巧搭建的橋梁，巧妙地連接著數據與模型參數這兩片看似隔絕的大陸，讓它們得以相互對話、相互啟示，為我們揭示隱藏在數據背后的參數真相鋪就道路。

從拋硬幣實驗啟程：似然函數的概念演繹

想象一下，你手中握著一枚硬幣，滿懷好奇心地將其拋擲了 10 次，結果有 8 次正面朝上。此刻，一個疑問悄然浮現：這枚硬幣是否是公正無偏的呢？為了尋找答案，似然函數 L(θ|D) 隆重登場。在這里，θ 被賦予了硬幣正面朝上概率的含義，而 D 則代表著我們親眼目睹的“8 正 2 反”實驗結果。

似然函數 L(θ) = C(10, 8)θ?(1 - θ)2，以簡潔而精準的數學表達式，描繪出不同 θ 值下，得到這般實驗結果的可能性圖景。組合數 C(10, 8) 考慮了在 10 次拋擲中，8 次正面分布的不同組合方式，它是數據特征的數學化呈現；而 θ?(1 - θ)2 則深深扎根于參數 θ 的不同取值，反映出在特定概率假設下，實驗結果發生的內在驅動。

深度剖析：似然函數與概率分布的精妙區分

似然函數與概率分布共享著相似的數學外觀，但它們背后蘊含的統計學哲理卻截然不同，宛如鏡像雙生子般各自獨立又相互映照。

概率分布，恰似一位神機妙算的預言家，在參數 θ 已知的前提下，憑借其數學形式精準預測數據 D 可能呈現的面貌。這里，參數 θ 是穩固不變的基石，而數據 D 則是變幻莫測的云彩，隨著每次實驗的不同而變換身姿。

然而，似然函數 L(θ|D) 則反轉了視角，化身成為一位敏銳的偵探。當實驗數據 D 已經塵埃落定，“8 正 2 反” 的結果擺在眼前，似然函數便以這既定的數據為線索，在參數 θ 的廣闊空間中四處探尋，挖掘出哪些 θ 值更有可能催生出這般數據。此時，數據 D 成為堅定不移的燈塔，而參數 θ 則是在探索海域中不斷試錯的船只。

最大似然估計：參數尋優的閃耀明珠

在似然函數構建的參數可能性圖景中，最大似然估計（Maximum Likelihood Estimation，MLE）宛如一顆璀璨奪目的明珠，熠熠生輝。MLE 的核心使命，就是在 θ 的茫茫可能性中，精準定位那個能使似然函數 L(θ|D) 達到巔峰的 θ 值。換言之，它致力于尋覓出那個最有可能“催生”出我們所觀測到的數據 D 的參數 θ。

回到拋硬幣的情境中，當 θ = 0.8 時，似然函數 L(θ) 攀登至頂峰。這絕非巧合，而是深刻邏輯的必然結果。因為若硬幣正面朝上的概率本就高達 0.8，那么在 10 次拋擲中斬獲 8 次正面，自然是極為合理且預期之中的結果。此時，最大似然估計θ? = 0.8 就成為了我們對硬幣公正性探究的有力結論 —— 這枚硬幣大概率是不公正的，其正面朝上概率更傾向于 0.8。

方法論升華：最大似然估計的統計學地位

最大似然估計并非只是拋硬幣游戲中的玩物，它在頻率學派的統計學體系中占據著舉足輕重的核心地位。頻率學派，作為統計學領域中追求客觀真理的一支重要力量，堅信通過反復實驗與觀測，能夠從數據中逐步逼近參數的真實值。而最大似然估計正是這一信念的完美踐行者。它以似然函數為利刃，披荊斬棘，斬斷數據與參數之間的混沌關聯，為我們呈現出那個“最有可能”的參數候選。

在實際應用的廣闊天地里，最大似然估計更是大顯身手。無論是醫學研究中探尋疾病風險因素與發病概率之間的微妙關聯，還是金融工程里解析市場波動數據以估算資產收益模型的參數，亦或是生物學領域利用觀測數據揭示物種進化參數的奧秘，最大似然估計都以其簡潔、直觀且堅實的理論基礎，成為統計分析的首選利器之一，助力學者們在數據的迷霧中照亮參數真相的彼岸。

醫學試驗中的統計學派別之爭：頻率派與貝葉斯派的博弈

在醫學試驗的舞臺上，頻率派和貝葉斯派的交鋒成為了統計學界爭論的焦點。以新藥有效性測試為例，兩派方法論的碰撞，為我們呈現了不同的思維方式和決策路徑。

頻率派：假設檢驗與 p 值的嚴謹之道

頻率派在醫學試驗中，采取嚴謹的假設檢驗流程。原假設 H0 通常設定為“新藥無效”，即新藥與安慰劑在療效上無差異。研究者精心設計試驗，將患者隨機分配至實驗組和對照組，確保兩組在基線特征上具有可比性。隨后收集數據，比較兩組的療效指標差異，如好轉率、治愈時間等。

p 值成為了判斷新藥是否有效的關鍵指標。如果 p 值小于 0.05，意味著在假設新藥無效的前提下，觀測到當前數據（例如實驗組好轉率比對照組高 10%）或更極端情況的概率不足 5%。頻率派據此認為，這樣的結果在原假設成立時極為罕見，從而傾向于拒絕 H0，認定新藥具有顯著療效。然而，頻率派方法存在局限性，其對 p 值的過度依賴可能導致決策的機械性。例如，當 p 值為 0.051 時，研究者可能因未達到顯著性水平而無法拒絕原假設，但這一結果與 p 值為 0.049 的情況在實際意義上可能相差無幾，卻在決策上形成天壤之別。此外，頻率派在解釋結果時相對保守，他們不會直接給出“新藥有效的概率是多少”，而僅能表明“拒絕或不拒絕原假設”。

貝葉斯派：先驗與后驗的融合之道

貝葉斯派的試驗方法更具靈活性，他們積極引入先驗信息，將其與試驗數據有機結合。先驗信息可以源自前期臨床試驗、動物實驗、體外實驗或專家經驗等，反映在試驗開始前對新藥療效的主觀認知。例如，根據以往類似藥物的療效數據，研究者可能設定新藥有效的先驗概率為 0.5。

貝葉斯派通過貝葉斯公式，將先驗概率與似然函數（即在不同療效假設下觀測到當前數據的概率）相結合，計算出后驗概率。后驗概率直觀地反映了在當前試驗數據下，新藥有效的概率。假設經過計算，后驗概率高達 0.9，這便強有力地表明新藥具有顯著療效。貝葉斯派的這一方法優勢在于能夠綜合多源信息，尤其在數據量有限時，先驗信息的融入可增強分析的穩健性。同時，后驗概率的直接解讀更契合醫學決策者的實際需求，便于他們根據概率結果制定合理的藥品審批、臨床應用或進一步研發決策。

頻率派與貝葉斯派的聯合應用：優勢互補的務實之道

在實際醫學研究中，頻率派與貝葉斯派并非對立，而是互為補充。一種常見的聯合應用模式是，在試驗設計階段，運用頻率派方法確定樣本量、計算檢驗效能等，確保試驗具有足夠的統計學效力去檢測新藥的潛在療效。而在試驗結果的分析與解釋階段，則引入貝葉斯思維，將當前試驗數據與歷史數據、專家意見等相結合，計算后驗概率，為決策提供更全面的依據。

例如，在罕見病藥物試驗中，由于患者招募困難，樣本量往往較小。此時，頻率派的假設檢驗可能因樣本量不足而難以達到顯著性水平。貝葉斯方法則可納入前期研究的先驗信息，提高分析的效率和結論的可靠性。此外，在藥物研發的早期階段，貝葉斯方法適合對多種潛在藥物進行快速篩選和決策；而在確證性試驗和監管審批階段，頻率派的假設檢驗提供了客觀、標準化的決策依據，增強了結論的可信度和接受度。

兩派的融合應用已成為現代醫學統計的發展趨勢，為醫學試驗的設計、分析與決策提供了更加強大、靈活且實用的工具。醫生、研究人員和決策者通過合理運用兩派方法，能夠更準確地評估藥物療效，加速新藥研發進程，最終使患者受益。

統計學在現實中的應用

統計學作為一門研究數據收集、分析和解釋的科學，其理論和方法在各個領域都發揮著不可替代的作用。通過理解統計學的基礎概念，我們可以深入剖析眾多統計方法背后的原理，并將其應用于解決實際問題。

統計方法的現實演繹

假設檢驗：決策的科學依據

假設檢驗是統計學中用于判斷某一假設是否成立的重要工具。其核心在于比較觀測數據在原假設條件下的極端程度，即通過計算 p 值來量化觀測結果的罕見性。例如，在醫學研究中評估一種新藥的療效時，研究者會設定原假設為“新藥無效”。通過精心設計的試驗收集數據后，計算出的 p 值能夠反映：假設新藥確實無效，那么觀測到當前試驗結果（例如實驗組患者的康復率比對照組高出一定比例）或更極端結果的概率。若 p 值小于預設的顯著性水平（通常為 0.05），則意味著在原假設成立的前提下，觀測結果極為罕見，進而有理由拒絕原假設，認為新藥可能具有顯著療效。這一方法為醫學研究提供了科學的決策依據，幫助篩選出真正有效的治療方法。

回歸分析：探索變量間的關系

回歸分析聚焦于研究條件期望 E(Y∣X) 隨自變量 X 變化而變化的規律。在社會科學研究中，回歸分析被廣泛應用于探究復雜的社會現象。以研究教育程度對收入水平的影響為例，通過收集大量個體的教育年限和收入數據，構建回歸模型能夠量化教育程度每提升一年，收入預期平均增長的幅度。同時，回歸分析還能控制其他變量（如工作年限、地域差異等），從而更準確地揭示教育程度與收入之間的凈關系。這為政策制定者提供了有力的支持，助力制定合理的教育政策，以促進社會公平與經濟發展。

貝葉斯統計：融合先驗與數據的智慧

貝葉斯統計通過結合先驗分布和似然函數，更新出后驗分布，實現了“用數據不斷修正和完善信念”的動態過程。在金融風險評估領域，貝葉斯方法展現出獨特優勢。假設我們要評估某只股票未來下跌的風險，初始的先驗分布可能基于歷史數據、行業趨勢以及宏觀經濟環境等因素構建。隨著新的市場數據不斷涌入，如公司季度財報的發布、重大政策的出臺等，通過貝葉斯公式更新后的后驗分布能夠更精準地反映當前市場環境下該股票下跌的概率。這種實時更新的特性使貝葉斯統計成為金融分析師手中的利器，幫助投資者更科學地管理投資組合風險。

統計學的強大根基與哲學思考

統計學之所以具備如此強大的應用能力，根本原因在于它運用數學語言精準地刻畫了人類面對不確定性時的理性決策過程。在現實世界中，不確定性無處不在：醫學研究中藥物的實際療效、金融市場的波動、人工智能模型對未知數據的預測等。概率分布為我們提供了一種全面且嚴謹的不確定性描述方式，使我們能夠清晰地把握事件可能的走向及其可能性大小；期望則進一步將不確定性濃縮為一個簡潔的數值，便于我們在決策時進行量化比較和權衡。這些核心概念共同構成了統計學大廈的基石，使其能夠在各個領域中發揮關鍵作用。

從更深層次的哲學角度審視，頻率派與貝葉斯派對“不確定性”本質的爭論，實際上揭示了人類認知世界的兩種不同視角。頻率派主張不確定性是客觀存在的現象，能夠通過長期頻率的穩定規律來揭示；而貝葉斯派則認為不確定性更多地反映了人類對世界的主觀認知局限，需要借助先驗信息和數據不斷修正和完善。這種哲學層面的思考不僅豐富了統計學的理論內涵，也為我們理解不同統計方法的應用場景和局限性提供了深刻的洞見。

統計思維的日常生活啟示

統計學的智慧并非高不可攀，而是與我們的日常生活息息相關。當我們看到“統計顯著”這樣的專業術語時，不妨深入探究其背后的 p 值原理：究竟是觀測結果在何種假設下被認為極不可能，從而促使研究者得出顯著性結論？當我們聽到“平均預期收益”時，應能夠聯想到期望值的加權平均本質，意識到這并非對未來確定收益的承諾，而是在多次決策中基于概率和收益值的長期平均預期。這種對統計術語和概念的深入理解，能夠幫助我們更理性地解讀各種信息，避免被片面的數據或結論誤導。

更重要的是，統計思維培養了我們用概率的眼光看待世界的思維方式。生活中絕大多數決策場景都充滿了不確定性：選擇投資項目、規劃職業發展路徑、評估健康風險等。統計思維使我們能夠基于有限的信息和數據，合理地量化各種可能結果的概率和影響，從而在不確定性中做出最優決策。它提醒我們承認未知的存在，但也賦予我們通過分析和推理去探索未知、把握未來的勇氣和智慧。

總之，統計學不僅是學術研究和專業領域中的強大工具，更是一種能夠深刻改變我們思維方式、提升決策質量的智慧源泉。通過理解并運用統計學的核心概念和方法，我們能夠在復雜多變的世界中更加理性、自信地面對各種挑戰和選擇。