【數據結構 · 初階】- 快速排序

一.?Hoare 版本

1. 單趟

2. 整體

3. 時間復雜度

4. 優化（搶救一下）

4.1 隨機選 key

4.2 三數取中

二. 挖坑法

格式優化

三. 前后指針（最好）

四. 小區間優化

五. 改非遞歸

快速排序是 Hoare 提出的一種基于二叉樹結構的交換排序方法。統一排升序

一.?Hoare 版本

1. 單趟

目的：選出一個關鍵字/關鍵值/基準值 key，把他放到排好序后，最終在的位置
key 都喜歡在最左/右邊，其他位置不好排

例如這樣的數組：

單趟結束后要達成這樣的效果：（選擇，插入，冒泡排序的單趟沒有這種附加效果）
此時6就在排好序后，所在的位置

實現：
R 往左走，找比 key 小的；L 往右走，找比 key 大的，相等無所謂。都找到之后，交換。直至相遇
結論：key 在左，讓 R 先走，能保證相遇位置一定比 key 小。? ? ? ? key 在右，讓 L 先走。
相遇位置既然比 key 小，就把 key 換到左邊

? ??
? ??

void QuickSort(int* a, int left, int right)
{int begin = left, end = right;int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]) // 右邊找小right--; // 且要防止本來就有序，right 飄出去while (left < right && a[left] <= a[keyi]) // 左邊找大left++;Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);keyi = left;
}

易錯：
? ? ? ? 1. 不能認為外面的 while 判斷過了，里面就不用判斷。里面的 while 會多走幾次，left 和 right 的相對位置變了，所以要再加判斷。?
? ? ? ? 2. 一定是 >= 否則可能出現死循環

2. 整體

遞歸：
上面排好單趟，被分成三段區間，[begin, keyi-1] keyi [keyi+1, end]。左右區間都無序，遞歸左區間。
選出 key 分成左右區間 …… 左區間有序，遞歸右區間。右區間有序，整體有序
遞歸返回條件：區間只剩一個值或區間不存在

遞歸的過程雖然圖上像是分出來了，其實都是在原數組上走的

和二叉樹的前序很像。單趟排是處理根（key），再處理左子樹（左區間），右子樹（右區間）

void QuickSort(int* a, int left, int right)
{// 遞歸返回條件if (left >= right) // = 是只剩一個值。> 是沒有值return;int begin = left, end = right;int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]) // 右邊找小right--; // 且要防止本來就有序，right 飄出去while (left < right && a[left] <= a[keyi]) // 左邊找大left++;Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);keyi = left;// 遞歸 [begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}

3. 時間復雜度

理想情況下：（小于）N * logN

N 個數，最終接近滿二叉樹 ==》logN

當 N = 100W，只需遞歸 20 層????????N = 10億，遞歸 30 層? ? ? ? 空間消耗不大，每層減的數也不大
最終每一層也還是 N 的量級

最壞：O( N^2 ) 搶救后忽略? ? ? ? 已經順/逆序

遞歸 N 層，建立 N 個棧幀，會棧溢出

4. 優化（搶救一下）

影響快排性能的是 keyi
keyi 越接近中間的位置，越二分，越接近滿二叉樹，深度越均勻，效率越高

不是讓左邊的值做 key ，而是讓 key 在最左邊的位置

4.1 隨機選 key

（生成位置% 區間大小）+ 左邊

void QuickSort(int* a, int left, int right)
{// 遞歸返回條件 ......int begin = left, end = right;// 優化1.隨機選 keyint randi = left + (rand() % (left - right));Swap(&a[left], &a[randi]); // 還是讓最左邊做 keyint keyi = left;while (left < right){ ...... }
}

管你有序無序，都把你變成無序

? ? ?

4.2 三數取中

有序 / 接近有序的情況下，選中間位置做 key 最好。但不一定是有序 / 接近有序
三數取中：選左右中 3個位置，不是最小，也不是最大的數的位置? ? ? ? 兩兩比較

int GetMidNumi(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]) // mid 不是中間，是最大的。{return left; // 剩下兩個：left 和 right 大的就是中間}else{return right;}}else // a[left] > a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]) // mid 是最小的{return left; // 剩下兩個：left 和 right 小的就是中間}else{return right;}}
}// 快速排序
void QuickSort(int* a, int left, int right)
{// 遞歸返回條件 ......int begin = left, end = right;// 優化2.三數取中int midi = GetMidNumi(a, left, right);Swap(&a[midi], &a[left]);int keyi = left;while (left < right){ ...... }
}

? ? ?

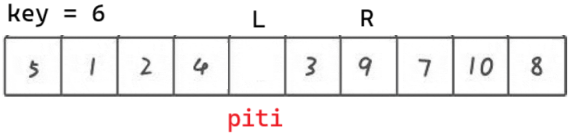
二. 挖坑法

先將第一個數據存放在臨時變量 key 中，形成一個坑位

piti 在左，不用想，肯定讓 right 先走

right 找到比 key 小的后，把 a[right] 扔到坑里，自己變成坑。left?走。

left?找到比 key 小的后，把 a[left] 扔到坑里，自己變成坑。right 走。

重復以上過程，直到 left 和 right 相遇。相遇點一定是坑，再把 key 扔到坑里

? ?
? ?

void QuickSort2(int* a, int left, int right)
{// 遞歸返回條件if (left >= right)return;int begin = left, end = right;// 優化2.三數取中int midi = GetMidNumi(a, left, right);Swap(&a[midi], &a[left]);int piti = left;int key = a[left];while (left < right){while (left < right && a[right] >= key) // 右邊找小right--;a[piti] = a[right]; // 扔到左邊的坑piti = right; // 自己成新的坑，坑到右邊去了while (left < right && a[left] <= key) // 左邊找大left++;a[piti] = a[left]; // 扔到右邊的坑piti = left; // 自己成新的坑，坑到左邊去了}a[piti] = key;// 遞歸 [begin, piti-1] piti [piti+1, end]QuickSort2(a, begin, piti - 1);QuickSort2(a, piti + 1, end);
}

格式優化

如果寫單趟，上面的寫法就可以

快排的遞歸框架是不變的，變的是單趟

// Hoare 單趟
int PartSort1(int* a, int left, int right)
{// 三數取中int midi = GetMidNumi(a, left, right);Swap(&a[midi], &a[left]);int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]) // 右邊找小right--;while (left < right && a[left] <= a[keyi]) // 左邊找大left++;Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);keyi = left;return keyi;
}// 挖坑 單趟
int PartSort2(int* a, int left, int right)
{// 三數取中int midi = GetMidNumi(a, left, right);Swap(&a[midi], &a[left]);int piti = left;int key = a[left];while (left < right){while (left < right && a[right] >= key) // 右邊找小right--;a[piti] = a[right]; // 扔到左邊的坑piti = right; // 自己成新的坑，坑到右邊去了while (left < right && a[left] <= key) // 左邊找大left++;a[piti] = a[left]; // 扔到右邊的坑piti = left; // 自己成新的坑，坑到左邊去了}a[piti] = key;return piti;
}void QuickSort(int* a, int left, int right)
{if (left >= right)return;int keyi = PartSort2(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}

三. 前后指針（最好）

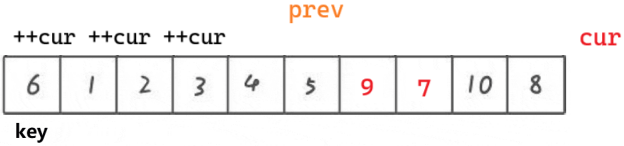
1. cur 找到比 key 小的值，++prev，交換 cur 和 prev 位置的數據，++cur
2. cur?找到比 key 大的值，++cur

把比 key 大的值往右翻，比 key 小的值往左翻

? ?
? ?
? ?
? ?
? ?

1. prev 要么緊跟著 cur（prev 下一個就是 cur）
2. prev 跟 cur 中間隔著比 key 大的一段值

int PartSort3(int* a, int left, int right)
{// 三數取中int midi = GetMidNumi(a, left, right);Swap(&a[midi], &a[left]);int keyi = left;int prev = left, cur = left + 1;while (cur <= right) // [left, right]，所以是 <={if (a[cur] < a[keyi]){++prev;Swap(&a[cur], &a[prev]);++cur;}else{++cur;}}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}void QuickSort(int* a, int left, int right)
{if (left >= right)return;int keyi = PartSort3(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}

while (cur <= right)
{if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[cur], &a[prev]);++cur;
}

四. 小區間優化

小區間直接使用直接插入排序

希爾是當數據量特別大時，為了讓大數快速往后跳才用
堆排還要建堆，很麻煩
冒泡只有教學意義，現實中幾乎沒用
選擇排序，最好最壞都是 N^2，也沒用

上面說遞歸圖看著像二叉樹

當區間特別小時，遞歸的次數會非常多。
光最后一層的遞歸數，就是總遞歸數的1/2。倒數第二次占1/4。倒數第三層占1/8

如果小區間直接使用直接插入排序，遞歸數量會少很多。現實中遞歸的不均勻，但怎么說也減少了50%的遞歸數量

void QuickSort(int* a, int left, int right)
{if (left >= right)return;// 小區間優化 - 小區間直接使用插入排序if (right - left + 1 > 10) // [left, right]左閉右閉區間，要 +1{int keyi = PartSort3(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}else{InsertSort(a + left, right - left + 1);}
}

不能寫成：InsertSort(a, right - left + 1)

正確。但如果是這樣就出錯了：

[ left , right ] 左閉右閉區間，要 +1

五. 改非遞歸

遞歸的問題：1. 效率（影響不大）? ? ? ? 2. 遞歸太深，棧溢出。不能調試

遞歸改非遞歸：
? ? ? ? 1. 直接改循環。原來正著走，遞歸逆著來（簡單）。eg：斐波那契數列。
? ? ? ? 2. 用棧輔助改循環。（難）eg：二叉樹

遞歸里，實際是用下標來分割子區間
遞歸里參數條件變化的是什么，棧里面存的就是什么。具體情況具體分析

思路：
? ? ? ? 1. 棧里面取一段區間，單趟排序
? ? ? ? 2. 單趟分割子區間入棧
? ? ? ? 3. 子區間只有一個值、不存在時就不入棧

為了和遞歸的過程一樣，棧里先入右區間，再入左區間。這樣就先排好左區間，再排好右區間
在棧里取單個區間時，若想先取左端點、再取右端點，就要先入右端點、再入左端點。

void QuickSortNonR(int* a, int left, int right)
{ST st;STInit(&st);STPush(&st, right);STPush(&st, left);while (!STEmpty(&st)){int begin = STTop(&st);STPop(&st);int end = STTop(&st);STPop(&st);int keyi = PartSort3(a, begin, end);// [begin,keyi-1] keyi [keyi+1, end]if (keyi + 1 < end){STPush(&st, end);STPush(&st, keyi + 1);}if (begin < keyi - 1){STPush(&st, keyi - 1);STPush(&st, begin);}}STDestroy(&st);
}

2 個 if 相當于遞歸的返回條件

本篇的分享就到這里了，感謝觀看，如果對你有幫助，別忘了點贊+收藏+關注。
小編會以自己學習過程中遇到的問題為素材，持續為您推送文章