1. 拉普拉斯算子

在該系列的第八篇文章中，我們曾經介紹過在二維空間拉普拉斯算子的定義為：

這是對函數? ?的二階偏導數之和。

2. 拉普拉斯算子的傅里葉變換及其推導

在該系列的第三十二篇文章中，我們曾給介紹過下面的公式

二維連續傅里葉變換：

二維連續傅里葉逆變換：

下面，我們嘗試推導一下拉普拉斯算子在頻域中的表示。首先考慮傅里葉變換的性質，特別是微分運算的傅里葉變換性質：

• 一階微分：在空間域中對 x 方向的微分變換為：

• 二階微分：在空間域中對 x 方向的二階微分變換：

同理，

現在，可以直接將拉普拉斯算子作用在? ?上的結果進行傅里葉變換：

在頻域中，由之前介紹過的公式可知? ?的傅里葉變換是? ，即?

拉普拉斯算子的作用等價于對? ?乘以一個因子：

這個乘積意味著：頻率越高（u 或 v 越大），乘的因子絕對值越大，也就是高頻成分被放大。因此頻域中的拉普拉斯算子常用于邊緣檢測、銳化等圖像處理任務。

3. 使用 OpenCV C++ 實現頻域的拉普拉斯算子

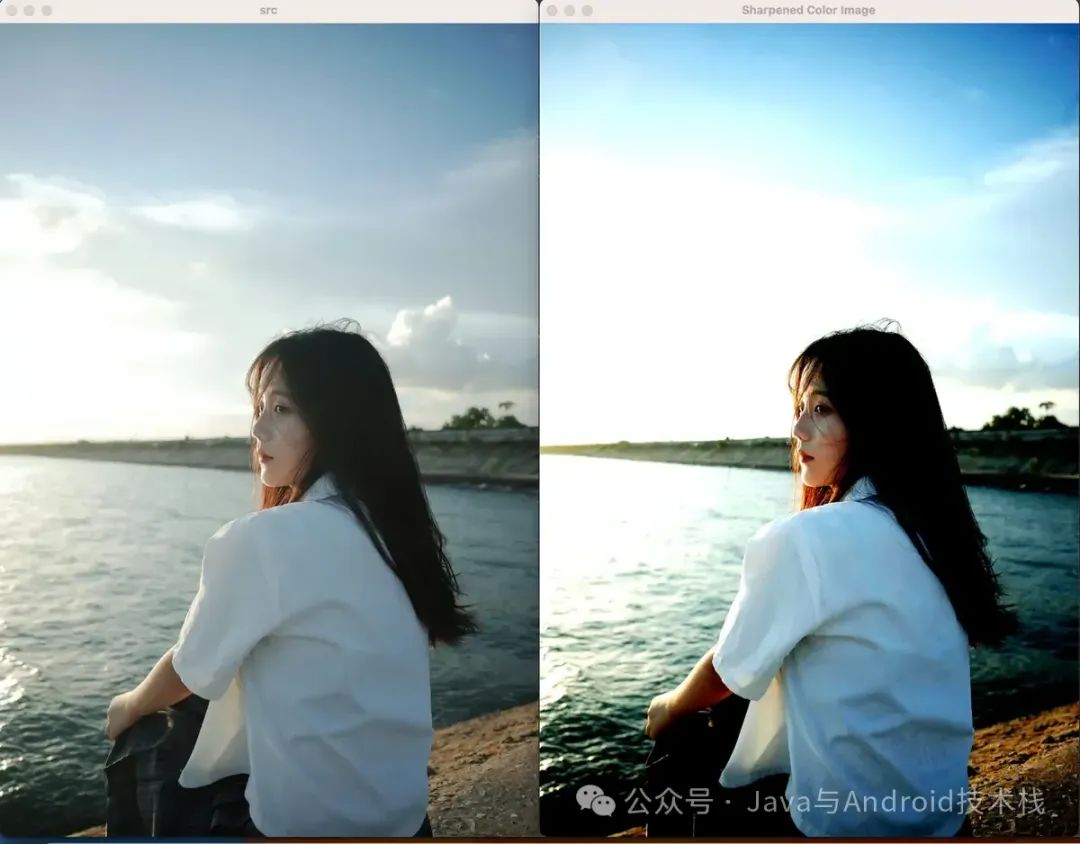
下面的例子，實現頻域拉普拉斯算子，并且對原圖進行銳化。

在頻域中，銳化操作相當于將原圖頻譜與拉普拉斯響應疊加。具體公式為：

其中 k 是一個控制銳化強度的正數。從空間域視角，這等價于：

#include?<opencv2/opencv.hpp>
#include?<iostream>usingnamespace?cv;
usingnamespacestd;// 創建頻域拉普拉斯濾波器
Mat?createLaplacianFilter(Size size)?{Mat laplacianFilter = Mat::zeros(size, CV_32FC2);int?center_row = laplacianFilter.rows /?2;int?center_col = laplacianFilter.cols /?2;float?factor = (2?* CV_PI) * (2?* CV_PI);?// 計算 (2*PI)^2for?(int?i =?0; i < laplacianFilter.rows; i++) {for?(int?j =?0; j < laplacianFilter.cols; j++) {float?u = (float)(i - center_row);float?v = (float)(j - center_col);float?d_squared = u * u + v * v;laplacianFilter.at<Vec2f>(i, j)[0] = -factor * d_squared;?// ?(2π)^2(u^2+v^2)laplacianFilter.at<Vec2f>(i, j)[1] =?0;}}return?laplacianFilter;
}// 對單個通道應用頻域拉普拉斯銳化并返回處理后頻域圖像的幅度譜
Mat?processChannelAndGetProcessedMag(const?Mat& src, Mat& dst,?double?alpha)?{int?m = getOptimalDFTSize(src.rows);int?n = getOptimalDFTSize(src.cols);Mat padded;copyMakeBorder(src, padded,?0, m - src.rows,?0, n - src.cols, BORDER_CONSTANT, Scalar::all(0));// 創建頻域圖像容器 (復數)Mat planes[] = {Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F)};Mat complexImg;merge(planes,?2, complexImg);// 進行傅里葉變換 (DFT)dft(complexImg, complexImg);// 創建拉普拉斯濾波器Mat laplacianFilter = createLaplacianFilter(complexImg.size());// 應用拉普拉斯濾波器Mat resultFreq;mulSpectrums(complexImg, laplacianFilter, resultFreq,?0);// 計算處理后頻域圖像的幅度譜 (用于可視化)Mat magProcessed;Mat processedPlanes[2];split(resultFreq, processedPlanes);magnitude(processedPlanes[0], processedPlanes[1], magProcessed);magProcessed += Scalar::all(1);?// 避免 log(0)log(magProcessed, magProcessed);normalize(magProcessed, magProcessed,?0,?1, NORM_MINMAX);int?cx_processed = magProcessed.cols /?2;int?cy_processed = magProcessed.rows /?2;Mat?q0_processed(magProcessed, Rect(0,?0, cx_processed, cy_processed));Mat?q1_processed(magProcessed, Rect(cx_processed,?0, cx_processed, cy_processed));Mat?q2_processed(magProcessed, Rect(0, cy_processed, cx_processed, cy_processed));Mat?q3_processed(magProcessed, Rect(cx_processed, cy_processed, cx_processed, cy_processed));Mat tmp_processed;q0_processed.copyTo(tmp_processed);q3_processed.copyTo(q0_processed);tmp_processed.copyTo(q3_processed);q1_processed.copyTo(tmp_processed);q2_processed.copyTo(q1_processed);tmp_processed.copyTo(q2_processed);// 進行傅里葉逆變換Mat resultImg;idft(resultFreq, resultImg, DFT_REAL_OUTPUT);// 裁剪回原始圖像大小resultImg = resultImg(Rect(0,?0, src.cols, src.rows));// 歸一化到 0-255 并轉換為 CV_8UMat resultImg_normalized;normalize(resultImg, resultImg_normalized,?0,?255, NORM_MINMAX, CV_8U);// 銳化addWeighted(src, alpha, resultImg_normalized, (1?- alpha),?0, dst);return?magProcessed;
}int?main()?{Mat src = imread(".../girl.jpg");if?(src.empty()) {cout?<<?"無法加載圖像"?<<?endl;return-1;}// 通道分離vector<Mat> channels;split(src, channels);// 對每個通道應用頻域拉普拉斯銳化并獲取處理后頻域圖像的幅度譜double?alpha =?1.5;?// 銳化強度因子Mat sharpenedB, sharpenedG, sharpenedR;Mat processedMagB = processChannelAndGetProcessedMag(channels[0], sharpenedB, alpha);Mat processedMagG = processChannelAndGetProcessedMag(channels[1], sharpenedG, alpha);Mat processedMagR = processChannelAndGetProcessedMag(channels[2], sharpenedR, alpha);// 合并銳化后的通道vector<Mat> sharpenedChannels = {sharpenedB, sharpenedG, sharpenedR};Mat sharpenedImg;merge(sharpenedChannels, sharpenedImg);imshow("src", src);imshow("Processed Magnitude Spectrum (Blue Channel)", processedMagB);imshow("Processed Magnitude Spectrum (Green Channel)", processedMagG);imshow("Processed Magnitude Spectrum (Red Channel)", processedMagR);imshow("Sharpened Color Image", sharpenedImg);waitKey(0);return0;
}

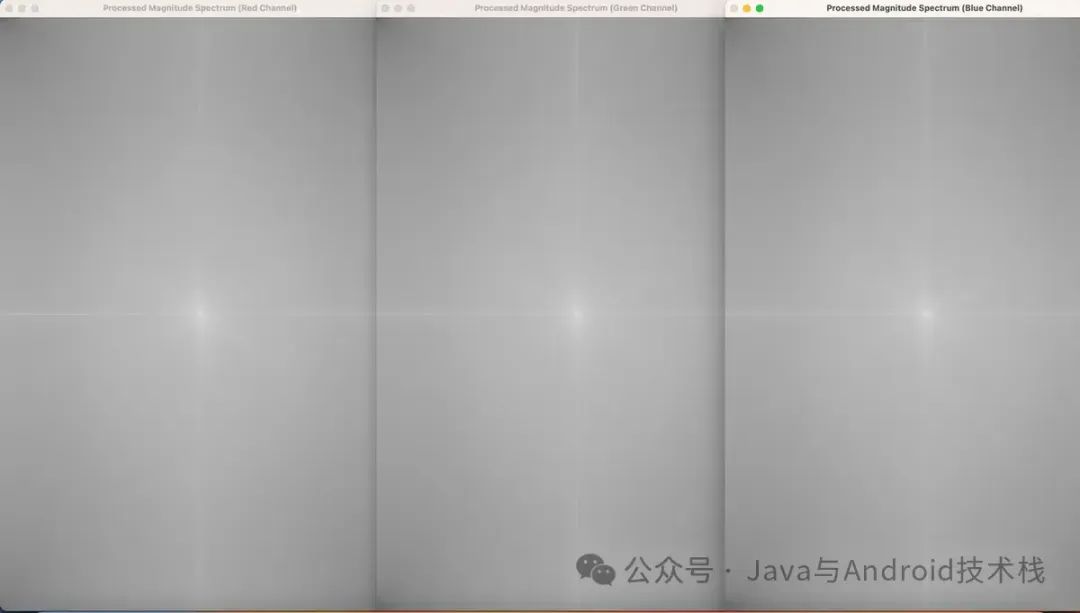
頻域拉普拉斯響應（即拉普拉斯濾波器作用后的圖像）

頻域拉普拉斯響應通常不適合直接顯示：

1. 拉普拉斯響應具有正負值對稱性（不是圖像強度）

• 拉普拉斯是一種二階微分算子，其結果表示圖像的邊緣變化強度和方向（凸或凹）。

• 拉普拉斯響應值可能是正的或負的，而標準圖像通道（如CV_8U）不能表達負值。

• 直接顯示會丟失符號信息：正負邊緣變得無法分辨。

2. 值域動態范圍極大，不適合線性可視化

頻域中經過拉普拉斯濾波后，結果的值可能在很大的范圍內波動（甚至數萬級別），遠遠超出 [0, 255]。直接轉換為 8 位圖像會導致：

• 要么強烈壓縮 → 對比度喪失（畫面幾乎全灰或全白）

• 要么飽和溢出 → 出現大片“過曝”或“過暗”現象

3. 響應是中間量，本身不代表直觀圖像內容。

所以，例子中展示了幅度譜，它是對頻域響應的一種可視化方式。

4. 總結

在頻域中，拉普拉斯算子通過傅里葉變換將空間域的微分操作轉換為頻域的乘法操作。主要用于增強圖像高頻成分以突出邊緣和細節，典型應用包括圖像銳化（通過逆變換疊加原圖與拉普拉斯響應）、邊緣檢測（抑制低頻保留高頻突變信號）、頻域濾波器設計（結合高低通濾波實現帶通或帶阻效果）以及圖像恢復中的正則化約束（抑制噪聲）。它是圖像增強與分析的非常有用的工具。