P1008 [NOIP 1998 普及組] 三連擊

# P1008 [NOIP 1998 普及組] 三連擊

## 題目背景

本題為提交答案題，您可以寫程序或手算在本機上算出答案后，直接提交答案文本，也可提交答案生成程序。

## 題目描述

將 $1, 2, \ldots , 9$ 共 $9$ 個數分成 $3$ 組，分別組成 $3$ 個三位數，且使這 $3$ 個三位數構成 $1 : 2 : 3$ 的比例，試求出所有滿足條件的 $3$ 個三位數。

## 輸入格式

無

## 輸出格式

若干行，每行 $3$ 個數字。按照每行第 $1$ 個數字升序排列。

## 輸入輸出樣例 #1

### 輸入 #1

```
無
```

### 輸出 #1

```
192 384 576
* * *
...

* * *
（剩余部分不予展示）
```

## 說明/提示

NOIP1998 普及組 第一題

#include<bits/stdc++.h>
int main(){int a,b,c;for(a=123;a<=333;a++){b=a*2;c=a*3;if((a/100+a/10%10+a%10+b/100+b/10%10+b%10+c/100+c/10%10+c%10==1+2+3+4+5+6+7+8+9)&&((a/100)*(a/10%10)*(a%10)*(b/100)*(b/10%10)*(b%10)*(c/100)*(c/10%10)*(c%10)==(1)*(2)*(3)*(4)*(5)*(6)*(7)*(8)*(9)))printf("%d %d %d\n",a,b,c);}return 0;
}

P1009 [NOIP 1998 普及組] 階乘之和

# P1009 [NOIP 1998 普及組] 階乘之和

## 題目描述

用高精度計算出 $S = 1! + 2! + 3! + \cdots + n!$（$n \le 50$）。

其中 `!` 表示階乘，定義為 $n!=n\times (n-1)\times (n-2)\times \cdots \times 1$。例如，$5! = 5 \times 4 \times 3 \times 2 \times 1=120$。

## 輸入格式

一個正整數 $n$。

## 輸出格式

一個正整數 $S$，表示計算結果。

## 輸入輸出樣例 #1

### 輸入 #1

```
3
```

### 輸出 #1

```
9
```

## 說明/提示

**【數據范圍】**

對于 $100 \%$ 的數據，$1 \le n \le 50$。

**【其他說明】**

注，《深入淺出基礎篇》中使用本題作為例題，但是其數據范圍只有 $n \le 20$，使用書中的代碼無法通過本題。

如果希望通過本題，請繼續學習第八章高精度的知識。

NOIP1998 普及組 第二題

#include<iostream>
#include<cstring>
using namespace std;
int n,a[90],b[90],c[90],f[90],d=0,len_a,len_b=1,len_c=1,len_ans,m=1;
string s;
int main(){cin>>n;b[0]=1; //初始化for(int i=1;i<=n;i++){ //計算i的階乘，已經算好了i-1的階乘len_a=0; //i的長度int p=i;while(p>0){ //把i存進a數組a[len_a++]=p%10;p/=10;}for(int j=0;j<len_a;j++) //計算a*b（i*（i-1）的階乘），即i的階乘，看不懂的網上查，我也不知道為什么for(int k=0;k<=len_b;k++)c[j+k]+=a[j]*b[k];for(int j=0;j<len_c;j++) //需要進位的就進位if(c[j]>9) c[j+1]+=c[j]/10,c[j]%=10;if(c[len_c]) len_c++; //看最高位要不要進位len_ans=len_b,len_b=len_c,m=max(m,len_c); //把len_b賦值給len_ans，修改len_b的值，m為i階乘的長度，看有沒有進位for(int k=len_c-1;k>=0;k--) b[k]=c[k]; //把c存進b數組，即存進i的階乘，下次循環b為i-1的階乘len_c=len_a+len_ans;memset(c,0,sizeof(c)); //清零c數組，準備計算下個階乘for(int j=0;j<m;j++){ //高精加，直接套模板f[j]+=b[j];if(f[j]>9) f[j+1]+=f[j]/10,f[j]%=10; //進位，注意不要寫成f[j+1]++，f[j]-=10;就因為這里wa了一個點}}while(!f[m]&&m>0) m--; //去掉首導零for(int i=m;i>=0;i--) cout<<f[i]; //倒序輸出return 0; 
}

P1014 [NOIP 1999 普及組] Cantor 表

# P1014 [NOIP 1999 普及組] Cantor 表

## 題目描述

現代數學的著名證明之一是 Georg Cantor 證明了有理數是可枚舉的。他是用下面這一張表來證明這一命題的：


我們以 Z 字形給上表的每一項編號。第一項是 $1/1$，然后是 $1/2$，$2/1$，$3/1$，$2/2$，…

## 輸入格式

整數$N$（$1 \leq N \leq 10^7$）。

## 輸出格式

表中的第 $N$ 項。

## 輸入輸出樣例 #1

### 輸入 #1

#include <bits/stdc++.h>
using namespace std; 
int main() {int n,k=1;cin>>n;while (n>k) {n=n-k;k++;}if(k%2==0) cout<<n<<"/"<<(k+1-n);else cout<<k+1-n<<"/"<<n;return 0;
} 

```
7
```

### 輸出 #1

```
1/4
```

## 說明/提示

- 2024-11-18 0:30 數據中加入了樣例，放在不計分的子任務 2 中。

P1044 [NOIP 2003 普及組] 棧

# P1044 [NOIP 2003 普及組] 棧

## 題目背景

棧是計算機中經典的數據結構，簡單的說，棧就是限制在一端進行插入刪除操作的線性表。

棧有兩種最重要的操作，即 pop（從棧頂彈出一個元素）和 push（將一個元素進棧）。

棧的重要性不言自明，任何一門數據結構的課程都會介紹棧。寧寧同學在復習棧的基本概念時，想到了一個書上沒有講過的問題，而他自己無法給出答案，所以需要你的幫忙。

## 題目描述


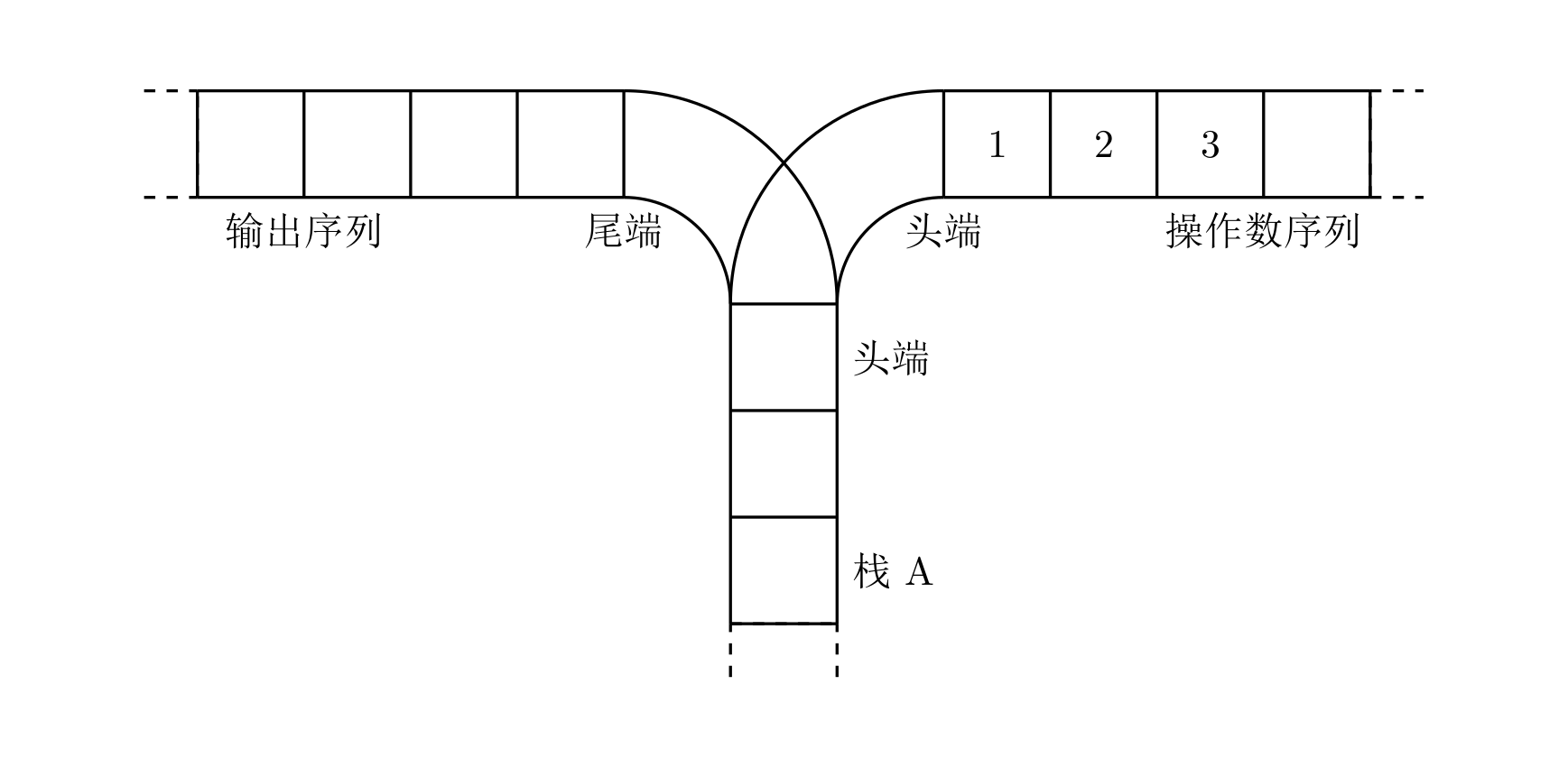
寧寧考慮的是這樣一個問題：一個操作數序列，$1,2,\ldots ,n$（圖示為 1 到 3 的情況），棧 A 的深度大于 $n$。

現在可以進行兩種操作，

1. 將一個數，從操作數序列的頭端移到棧的頭端（對應數據結構棧的 push 操作）
2. 將一個數，從棧的頭端移到輸出序列的尾端（對應數據結構棧的 pop 操作）

使用這兩種操作，由一個操作數序列就可以得到一系列的輸出序列，下圖所示為由 `1 2 3` 生成序列 `2 3 1` 的過程。


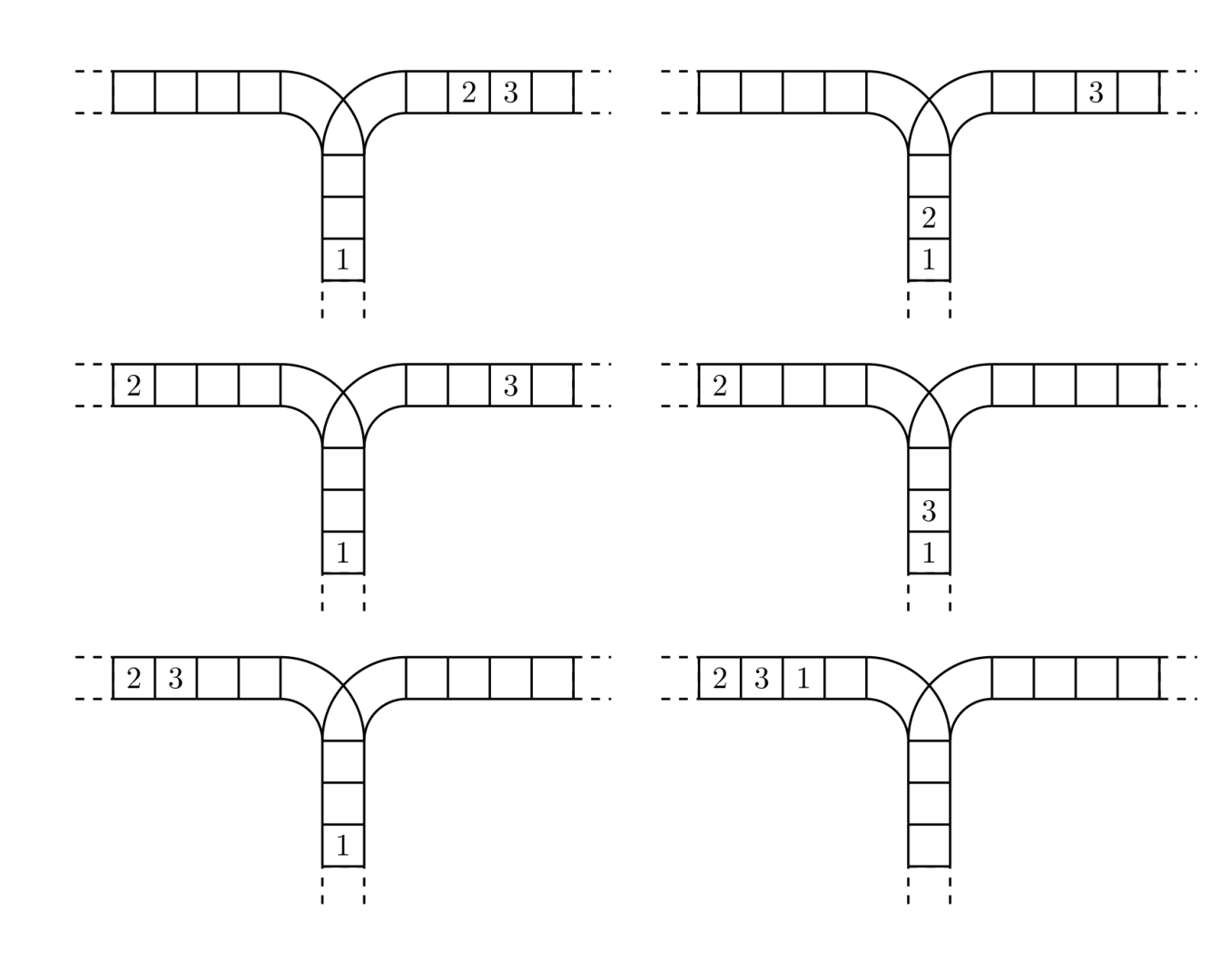
（原始狀態如上圖所示）

你的程序將對給定的 $n$，計算并輸出由操作數序列 $1,2,\ldots,n$ 經過操作可能得到的輸出序列的總數。

## 輸入格式

輸入文件只含一個整數 $n$（$1 \leq n \leq 18$）。

## 輸出格式

輸出文件只有一行，即可能輸出序列的總數目。

## 輸入輸出樣例 #1

### 輸入 #1

```
3
```

### 輸出 #1

```
5
```

## 說明/提示

**【題目來源】**

NOIP 2003 普及組第三題

//遞歸轉遞推  遞推做法 
#include<cstdio>
#define MAX_N 20
#define ll long long
using namespace std;
int n;
ll f[MAX_N][MAX_N];
int main()
{scanf("%d",&n);for(int i=0;i<=n;i++){f[0][i]=1;}for(int i=1;i<=n;i++){for(int j=i;j<=n;j++){if(i==j)f[i][j]=f[i-1][j];else f[i][j]=f[i][j-1]+f[i-1][j];}}printf("%lld",f[n][n]);return 0;
}

# P1024 [NOIP 2001 提高組] 一元三次方程求解

## 題目描述

有形如：$a x^3 + b x^2 + c x + d = 0$ ?這樣的一個一元三次方程。給出該方程中各項的系數（$a,b,c,d$ 均為實數），并約定該方程存在三個不同實根（根的范圍在 $-100$ 至 $100$ 之間），且根與根之差的絕對值 $\ge 1$。要求由小到大依次在同一行輸出這三個實根(根與根之間留有空格)，并精確到小數點后 $2$ 位。

提示：記方程 $f(x) = 0$，若存在 $2$ 個數 $x_1$ 和 $x_2$，且 $x_1 < x_2$，$f(x_1) \times f(x_2) < 0$，則在 $(x_1, x_2)$ 之間一定有一個根。

## 輸入格式

一行，$4$ 個實數 $a, b, c, d$。

## 輸出格式

一行，$3$ 個實根，從小到大輸出，并精確到小數點后 $2$ 位。

## 輸入輸出樣例 #1

### 輸入 #1

```
1 -5 -4 20
```

### 輸出 #1

```
-2.00 2.00 5.00
```

## 說明/提示

**【題目來源】**

NOIP 2001 提高組第一題

#include<cstdio>
double a,b,c,d;
double fc(double x)
{return a*x*x*x+b*x*x+c*x+d;
}
int main()
{double l,r,m,x1,x2;int s=0,i;scanf("%lf%lf%lf%lf",&a,&b,&c,&d);  //輸入for (i=-100;i<100;i++){l=i; r=i+1;x1=fc(l); x2=fc(r);if(!x1) {printf("%.2lf ",l); s++;}      //判斷左端點，是零點直接輸出。//不能判斷右端點，會重復。if(x1*x2<0)                             //區間內有根。{while(r-l>=0.001)                     //二分控制精度。{m=(l+r)/2;  //middleif(fc(m)*fc(r)<=0) l=m; else r=m;   //計算中點處函數值縮小區間。}printf("%.2lf ",r);  //輸出右端點。s++;}if (s==3) break;             //找到三個就退出大概會省一點時間}return 0;
}