---

---

一、棧

棧說白了就是一個盒子，你先放進去的東西后拿出來，實現棧除了可以使用棧的類Stack外，還可以使用鏈表
遵循先進先出，后進后出原則進行內容變化，重點是可以把遞歸轉換成棧
我們查看其源碼我們看到，它實質上是一個順序表即數組，有壓棧和出棧操作

1. 模擬實現棧

這次我們就不定義接口了，就直接寫MyStack類吧，然后實現一些方法
我們重點就來講壓棧和出棧，壓棧說白了就是先檢測你的數組有沒有滿，滿了就擴容，否則我們就直接讓有效元素個數對應的下標的數字等于我們壓入的數字（因為數組下標和實際位置差1的特性）
出棧就是先判斷數字是不是空的，如果不是我們直接讓有效數字個數減少，這樣我們再次壓入其他數字的時候就可以把原有數字覆蓋
其他方法操作下來，我們的時間復雜度都是O(1)

//MyStack類
public class MyStack {public int [] elem;public int usedSize;public MyStack() {this.elem = new int[2];}public void push(int val) {if (isFull()) {this.elem = Arrays.copyOf(elem, 2 * elem.length);}elem[usedSize] = val;usedSize++;}public boolean isFull() {return usedSize == elem.length;}public int pop(){if(isEmpty()){throw new IsEmptyException("空數組異常");}int ret = peek();usedSize --;return ret;}public boolean isEmpty(){return usedSize == 0;}public int peek(){if(isEmpty()){throw new IsEmptyException("空數組異常");}return elem[usedSize-1];}public int size(){if(isEmpty()){throw new IsEmptyException("空數組異常");}return usedSize;}@Overridepublic String toString() {return "MyStack{" +"elem=" + Arrays.toString(elem) +", usedSize=" + usedSize +'}';}
}//測試類
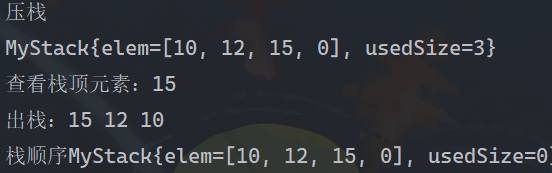
public static void main(String[] args) {MyStack myStack = new MyStack();System.out.println("壓棧");myStack.push(10);myStack.push(12);myStack.push(15);System.out.println(myStack);System.out.println("查看棧頂元素："+myStack.peek());System.out.print("出棧：");System.out.print(myStack.pop()+" ");System.out.print(myStack.pop()+" ");System.out.print(myStack.pop());System.out.println();System.out.println("棧順序"+myStack);Stack<Integer> stack = new Stack<>();}

打印結果就是這樣，看起來一切正常

2. 小試牛刀

1. 判斷一個棧的出棧順序是否為題目給定情況

題目鏈接
我們首先來講講這道題的核心思想是什么，根據題目要求
我們讓i下標等于pushV，j下標等于popV
我們就以：pushV：1 2 3 4 5 和popV：4 3 5 1 2來講解
我們先定義一個棧，叫stack，把右側看做棧頂
好，我們定義好了i下標和j下標，此時它們分別代表數字1和數字4
我們比較i下標的數字和j下標數字是否匹配，發現不匹配，將i下標當前指向的元素放入棧中，此時我們得棧數字有[1]，此時我們得i下標++，發現還是和j下標數字不匹配，繼續放元素到棧中，繼續++
直到[1,2,3,4]，發現棧中的棧頂元素為4，和j下標元素匹配，那好，我們就彈出棧頂元素4，此時棧中元素為[1,2,3]，此時j下標++向后走，走到數字3位置，此時我們再判斷，棧中元素是空的嗎，不是，我們還要繼續判斷相等，此時我們我們發現棧頂元素3和j下標當前的數字3匹配，我們棧頂元素繼續彈出，k++一下向后走，走到數字5的位置，此時棧中元素為[1,2]
此時再判斷，棧中元素是空的嗎，不是，那我們還要繼續判斷相等，此時這一輪循環走完了，我們的i要++一下，走到數字5的位置，此時棧頂元素是2，和當前j下標的數字不一樣，那我們是不是繼續要從pushV中放數字，好，我們放入數字5，此時棧中元素為[1,2,5]，棧頂元素和此時j下標的元素相等，我們此時彈出棧頂元素，此時j++向后走一位，走到1的位置，此時棧中元素為[1,2]，此時棧頂元素和j下標并不匹配，這一輪循環走完，i++了一下，此時i就超過了原來的數組范圍，大的循環走了出來，此時我們判斷棧中是否還存有元素，發現還是有元素，那我們就可以知道“4 3 5 1 2”這個出棧順序就不是原有合理順序
如果出棧順序是這樣popV：4 5 3 2 1 ，一樣的逐一的進行判斷，發現最后棧是空的，那它就是和題目要求成立
但是有個特殊情況，比如這樣：如果每個都匹配的情況 5 4 3 2 1 和 1 2 3 4 5
那內部進行判斷的時候我們就要加上限制條件棧不可以為空并且j位置不能超過原數組范圍，因為此時下標出了數組范圍再取元素就空數組異常了，i不用判斷是因為i有循環進行范圍約束而j卻沒有

public class Solution {/*** 代碼中的類名、方法名、參數名已經指定，請勿修改，直接返回方法規定的值即可** * @param pushV int整型一維數組 * @param popV int整型一維數組 * @return bool布爾型*/public boolean IsPopOrder (int[] pushV, int[] popV) {Stack <Integer> stack = new Stack<>();int i = 0;int j = 0;for(i = 0;i<pushV.length;i++){//大循環stack.push(pushV[i]);//還要考慮如果每個都匹配的情況 5 4 3 2 1 和 1 2 3 4 5while(!stack.empty() && j<= popV.length && stack.peek() == popV[j]){//內部循環stack.pop();j++;}}//看看stack空不空就行了return stack.empty();}
}

2. 括號匹配

題目鏈接
這個題目核心問題就是如何去直到括號在哪以及括號的個數的問題
我們就拿( [ ] )舉例，我們定義一個棧，把左括號存到里面去，棧中元素和右括號進行匹配，如果相等則彈出棧頂元素，以此類推，如果在彈出過程中第一次遇到不匹配的情況，不要猶豫直接返回false，肯定不是匹配了的
我們再拿(( )情況舉例，如果右括號你都匹配完了左括號還有剩余，那也是不匹配
還有( ))情況，左括號遍歷完了右括號還有剩余，也是不匹配

class Solution {public boolean isValid(String s) {Stack <Character> stack = new Stack<>();for(int i = 0 ;i<s.length();i++){//取出字符char ch = s.charAt(i);if(ch == '(' || ch == '{' || ch == '['){stack.push(ch);}else{//判空if(stack.empty()){return false;}//比較char chs = stack.peek();if(chs == '(' && ch == ')' || chs == '{' && ch == '}' || chs == '[' && ch == ']'){stack.pop();}else{//說明剩下的右邊的元素根本就不是括號，可能是其他字符//比如((??這樣return false;}}}//如果此時for循環走完了你的棧中還有元素，也就是說沒有匹配完if(!stack.empty()){return false;}//當上述所有條件頭部滿足，說明就刪完了，匹配成功return true;}
}

3. 逆波蘭表達式求值

題目鏈接
我們首先明白什么是逆波蘭表達式，我們正常的表達式是這樣的，比如2*(3+5)
但是計算機的計算器在計算的時候是不知道我們人類的運算符優先規則去算的，那是怎么搞的呢
你看，逆波蘭表達式核心就是把符號往后移，看我演示
設$M=(3+5)$，則M的逆波蘭表達式為$35+$，之后整體式子的逆波蘭表達式是$ 2M* $，帶入M后就是$2 35+ * $，那此時計算就是$ 3+5=8 $，再$2?8=16$
畫圖就是這樣的

那我們直接來寫題吧

class Solution {public int evalRPN(String[] tokens) {Stack<Integer> stack = new Stack();for(int i = 0;i<tokens.length;i++){if(!isOperator(tokens[i])){stack.push(Integer.parseInt(tokens[i]));}else{//注意兩個數的出棧順序int num1 = stack.pop();int num2 = stack.pop();switch(tokens[i]){case "+"://算出的結果要壓入棧中stack.push(num2+num1);break;case "-":stack.push(num2-num1);break;case "*":stack.push(num2*num1);break;case "/":stack.push(num2/num1);break;}}}return stack.pop();}private boolean isOperator(String operator){if(operator.equals("+")||operator.equals("-")||operator.equals("*")||operator.equals("/")){return true;}return false;}
}

4. 求最小棧元素

題目鏈接
就是要求棧中最小的元素，因為棧不可以倒著遍歷，因此我們只能用兩個棧，一個普通棧存數字，另一個最小值棧存放當前棧中最小數字
當我不斷的壓普通棧，如果壓的數字有比當前存放最小值的棧的棧頂元素小的話，最小值的棧頂元素就變成當前壓入普通棧大的元素
這樣當我普通棧出棧的時候，如果比我最小棧棧頂元素一樣，那就一起出，否則就只是普通棧出
這樣當我后續刪除普通棧元素時，每一次都能在最小棧中找到當前普通棧中的最小值

class MinStack {private Stack<Integer> stack;private Stack<Integer> minStack;;public MinStack() {stack = new Stack<>();minStack = new Stack<>();}public void push(int val) {//先壓入普通棧再判斷stack.push(val);//判空if(minStack.empty()){//最小值棧首次壓入元素minStack.push(val);}else{//只有當壓入普通棧的元素比最小值棧的棧頂元素小的時候//此時壓入普通棧的數字才要同時壓入最小值棧if( val <= minStack.peek()){minStack.push(val);}}}public void pop() {//判空if(stack.empty()){return;}//如果普通棧棧頂元素和最小值棧棧頂元素相等，要一起彈出int val = stack.pop();if(val == minStack.peek()){minStack.pop();}}public int top() {//判空if(stack.empty()){return -1;}return stack.peek();}public int getMin() {return minStack.peek();}
}

3. 單鏈表實現棧

入棧我們采用頭插法，出棧我們采用刪除頭節點方法，此時它們時間復雜度都是O(1)
假如你入棧采用尾插法，還要遍歷去找尾巴，麻煩，時間復雜度是O(n)
假如你對單鏈表的尾節點加上last引用，入棧沒問題了可是你出棧還不是要刪除尾節點，還不是要找其前一個節點，時間復雜度還是O(n)
但是，如果你采用雙向鏈表，就可以實現，而且雙向鏈表本身就有實現Deque接口，我們說過這是跟棧和隊列有關的接口

public class LinkedList<E>extends AbstractSequentialList<E>implements List<E>, Deque<E>, Cloneable, java.io.Serializable

使用雙向列表，我們就能保證出棧和入棧的時間復雜度都是O(1)

二、隊列

這個定義說白了就跟我們排隊一樣的，遵循先進先出后進后出
只不過分為普通隊列和雙端隊列
普通隊列是Queue類，而雙端隊列則是Deque類

當然，我們之前有講過，鏈表可以實現棧和隊列，那對于單鏈表如果去實現隊列
你給單鏈表的尾節點添加了Last引用，此時尾插法入隊和頭刪法出隊時間復雜度都是O(1)沒有問題，但是反之頭插法入隊和尾刪法出隊還是得知道尾節點的前驅節點，時間復雜度還是O(n)

1. 官方隊列類Queue

我們通過雙向鏈表創建Queue類Queue <Integer> queue = new LinkedList<>();

以下是各個方法測試

public static void main(String[] args) {Queue <Integer> queue = new LinkedList<>();System.out.println("入隊");queue.offer(15);queue.add(10);System.out.println("出隊");System.out.println(queue.poll());System.out.println(queue.remove());System.out.println("再次出隊，各個方法情況");System.out.println("不會拋出異常"+queue.poll());System.out.println("拋出異常"+queue.remove());System.out.println("查看隊頭元素，各個方法情況");System.out.println("不會拋出異常"+queue.peek());System.out.println("會拋出異常"+queue.element());}

關于入隊、出隊以及查看隊頭元素，都有各自的兩種方法，它們區別就是安全性問題
對于使用add、remove和element方法會拋出異常，而offer、poll和peek則不會，因此我們從安全性原則上去講，更推薦offer、poll和peek方法

2. 雙向鏈表模擬實現Queue類

入隊就采用尾插法，出隊就采用頭刪法，查看隊頭元素直接返回頭節點的數值

public class MyQueue {static class LinkedList{public int value;public LinkedList nextAddress;public LinkedList previousAddress;public LinkedList(int value) {this.value = value;}}public LinkedList head;public LinkedList last;public int usedSize;//入隊-->尾插法，遵循源碼public void offer(int data){LinkedList node = new LinkedList(data);if(head == null){head = last = node;}else{last.nextAddress = node;node.previousAddress = last;last = node;usedSize++;}}//出隊-->頭刪法public int poll(){if(head == null){throw new QueueEmptyException("空隊列異常");}int val = head.value;if(head.nextAddress == null){head = last = null;}else{head = head.nextAddress;head.previousAddress = null;usedSize--;}return val;}//查看隊頭情況public int peek(){if(head == null){throw new QueueEmptyException("空隊列異常");}return head.value;}public int size(){return usedSize;}public boolean isEmpty(){return head == null;}public void display(){LinkedList current = head;while(current != null){System.out.print(current.value+" ");current = current.nextAddress;}}
}//自定義異常QueueEmptyException類
public class QueueEmptyException extends RuntimeException{public QueueEmptyException() {}public QueueEmptyException(String message) {super(message);}
}//測試用例
public static void main(String[] args) {MyQueue myQueue = new MyQueue();System.out.println("入隊方法測試");myQueue.offer(10);myQueue.offer(15);myQueue.offer(22);myQueue.offer(30);myQueue.display();System.out.println();System.out.println("出隊方法測試");System.out.print(myQueue.poll()+" ");System.out.print(myQueue.poll()+" ");System.out.println();System.out.println("獲取隊頭元素方法測試");System.out.print("隊列情況：");myQueue.display();System.out.println();System.out.print("出隊：");System.out.println(myQueue.peek());System.out.print("獲取大小：");System.out.println(myQueue.size());System.out.print("判空：");System.out.println(myQueue.isEmpty());}

最中效果如下

3. 順序表模擬實現Queue類

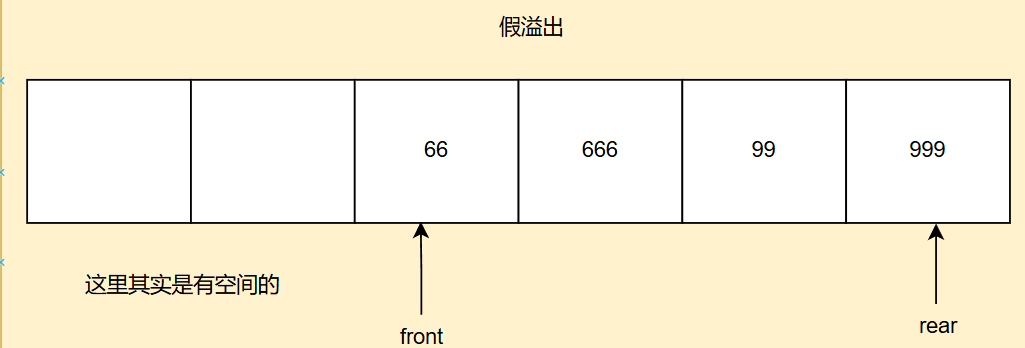
順序表會有一種情況，首先我定義隊頭指針front和隊尾指針rear，我每添加一個元素我的rear就往后走，直到到達邊界，走到末尾我們循環回到開頭，好，此時我要出隊出一些元素，此時我的front向后走了幾步，我此時再想放元素發現“滿了”
但真的滿了嗎，我不是剛剛才出隊幾個元素沒，誒，這就是數組的假溢出，因為你的rear隊尾指針走到頭了會誤以為滿了

Q1：還有，我們不是定義了隊頭隊尾指針嗎，你想我們開始為空的時候它們會在一起，數組滿了的時候它們也會在一起，如何區分呢
Q2：其次，我們既然要實現循環隊列，如何實現呢

• 解法一：添加size屬性標記
• 解法二：開始為空的時候我們標記成false，每一次入隊我們檢查front是否重合，如果重合就標記成true否則我們就正常添加元素
• 解法三：每一次存放數據的時候檢查rear的下一個是不是front，如果是我們就可以認為滿了，不能再放入元素

---

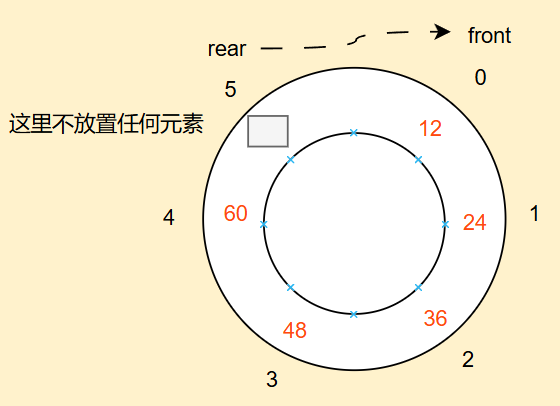
那如何從數組后面跳到前面呢，我們先來講講偏移量概念
如果你想從數組前面到達后面，我們就要(index+array.length-偏移量)%array.length
如果你想從數組后面到達前面，我們就要(index+偏移量)%array.length
偏移量指的就是你和你目標舉例多遠，比如4下標距離5下標距離是1，假如數組大小是4則3下標舉例0下標距離也是1

---

我們采用解法三去實現，這里給出一道相關的題題目鏈接

class MyCircularQueue {public int [] array;public int front;//頭public int rear;//尾 public MyCircularQueue(int k) {//示例中給三個能夠從一下標獲取元素，說明至少需要k+1個空間array = new int[k+1];}public boolean enQueue(int value) {if(isFull()){return false;}this.array[rear] = value;//不可以直接rear++，否則越界rear = (rear+1)%array.length;return true;}public boolean deQueue() {if(isEmpty()){return false;}front = (front+1)%array.length;return true;}public int Front() {if(isEmpty()){return -1;}return array[front];}public int Rear() {if(isEmpty()){return -1;}//此時還要判斷rear的位置，如果是0說明滿了回到了開頭//否則沒有滿就返回下標前一個數if(rear == 0){return array[array.length-1];}else{return array[rear-1];}}public boolean isEmpty() {if(rear == front){return true;}return false;}public boolean isFull() {if((rear+1)%array.length == front){return true;}return false;}
}

4. 雙端隊列

現在不管從哪邊入隊和出隊都可以了
而且我們看到Deque源碼中有peek和poll方法，證明其可以實現棧
而且還有數組型棧ArrayDeque，它也可以作為隊列

public static void main(String[] args) {Deque<Integer> deque = new LinkedList<>();deque.addFirst(11);deque.addFirst(22);deque.addLast(33);System.out.println(deque);System.out.print(deque.pollFirst()+" ");System.out.println(deque.pollLast());System.out.println("===實現棧===");Deque<Integer> deque1 = new LinkedList<>();deque1.push(11);deque.push(22);deque1.push(33);System.out.println(deque1);System.out.println("查看棧頂元素："+deque1.peek());System.out.println("彈出棧頂元素："+deque1.poll());System.out.println(deque1);System.out.println("===數組實現雙端棧===");Deque<Integer> deque2 = new ArrayDeque<>();deque2.push(11);deque2.push(55);deque2.push(88);System.out.println(deque2);System.out.println("查看棧頂元素："+deque2.peek());System.out.println("彈出棧頂元素："+deque2.poll());System.out.println(deque2);System.out.println("===數組實現隊列===");Deque<Integer> deque3 = new ArrayDeque<>();deque3.addFirst(42);deque3.addFirst(55);deque3.addLast(99);System.out.println(deque3);System.out.println("查看棧頂元素："+deque3.peek());System.out.println("彈出棧頂元素："+deque3.poll());System.out.println(deque3);}

5. 隊列實現棧

題目鏈接
我們這道題要使用兩個隊列，因為你的隊列是先進先出，而棧是先進后出，因此要有另一個隊列存出棧元素
怎么個出法呢？假設剛開始兩個隊列都為空，則我們默認把數字依次放入隊列一queue1中
下一次再放元素的時候哪一個隊列不是空的我們就放進哪個隊列中
出元素時，我們看哪一個隊列不是空的，我們就出除了出隊元素以外的元素

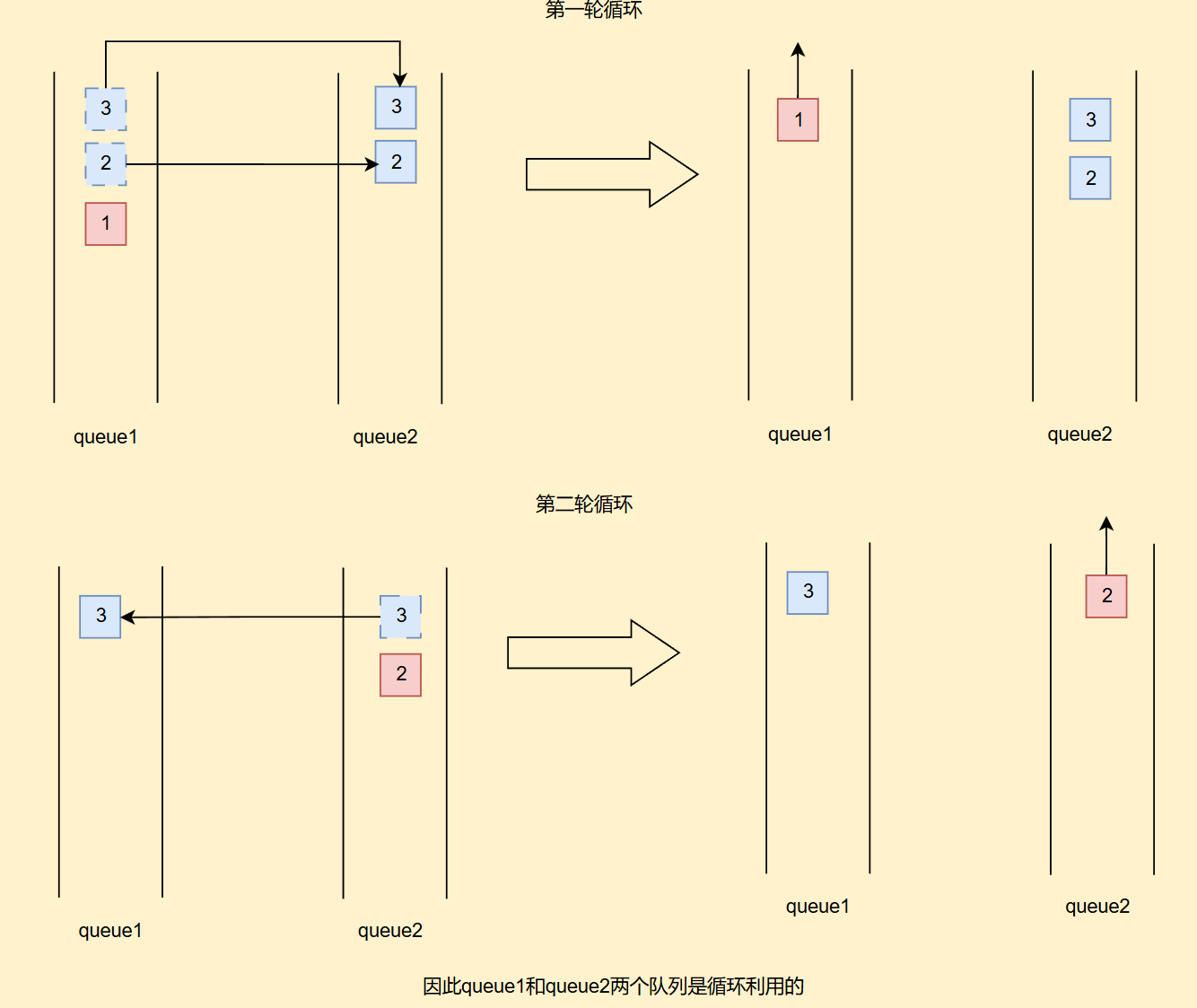
還有后續獲取“棧頂元素”時候，我們要定義一個中間變量temp，每次從一個棧中彈出元素的時候我們就把數字放在里面，直到最后一次彈出的數字就是我們想要的隊頭元素

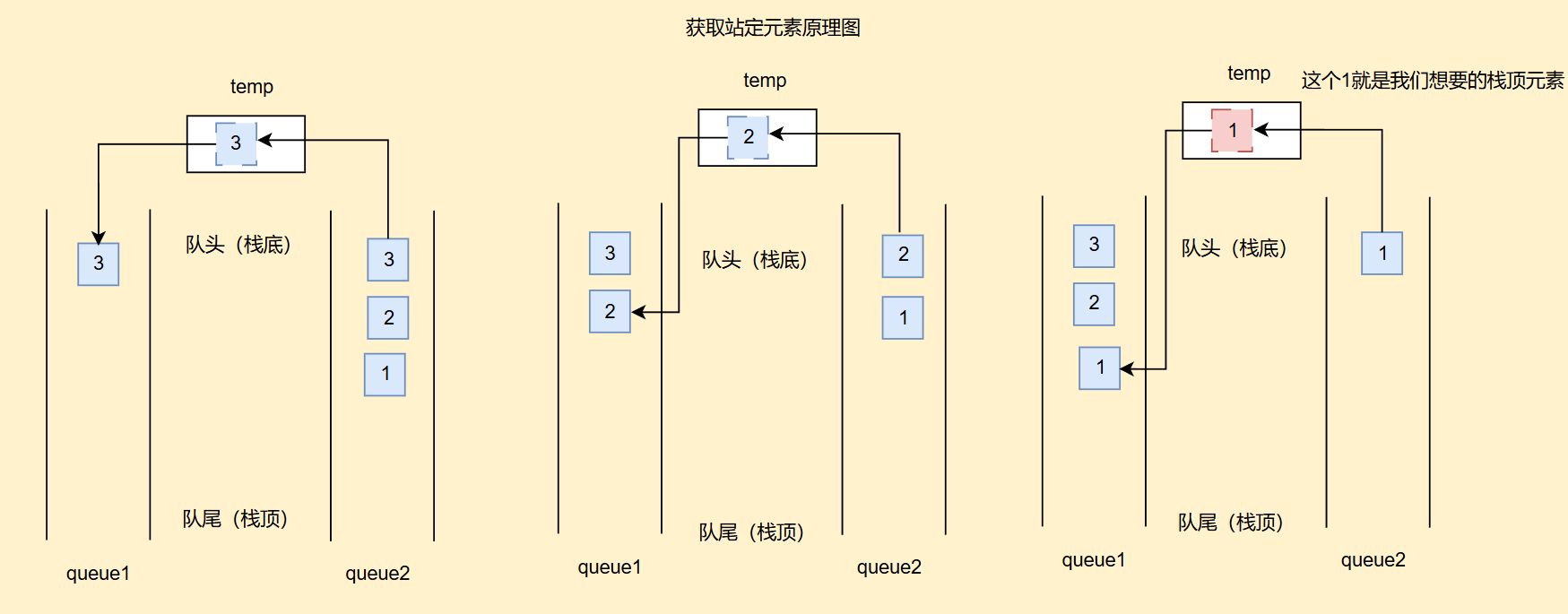
class MyStack {private Queue<Integer> qu1;//我用簡寫表示queue1private Queue<Integer> qu2;//同理public MyStack() {qu1 = new LinkedList<>();qu2 = new LinkedList<>();}public void push(int x) {if(qu2.isEmpty()){//qu2空qu1.offer(x);}else if(qu1.isEmpty()){//qu1空qu2.offer(x);}else{//同時為空qu1.offer(x);}}public boolean empty() {return qu1.isEmpty() && qu2.isEmpty();}public int pop() {if(empty()){return -1;}if(qu1.isEmpty()){int size = qu2.size();while(size-1 != 0){qu1.offer(qu2.poll());size--;}return qu2.poll();}else if(qu2.isEmpty()){int size = qu1.size();while(size-1 != 0){qu2.offer(qu1.poll());size--;}return qu1.poll();}return -1;}public int top() {if(empty()){return -1;}if(qu1.isEmpty()){int temp = 0;int size = qu2.size();while(size != 0){temp = qu2.poll();qu1.offer(temp);size--;}return temp;}else if(qu2.isEmpty()){int temp = 0;int size = qu1.size();while(size != 0){temp = qu1.poll();qu2.offer(temp);size--;}return temp;}return -1;}
}/*** Your MyStack object will be instantiated and called as such:* MyStack obj = new MyStack();* obj.push(x);* int param_2 = obj.pop();* int param_3 = obj.top();* boolean param_4 = obj.empty();*/

6. 棧實現隊列

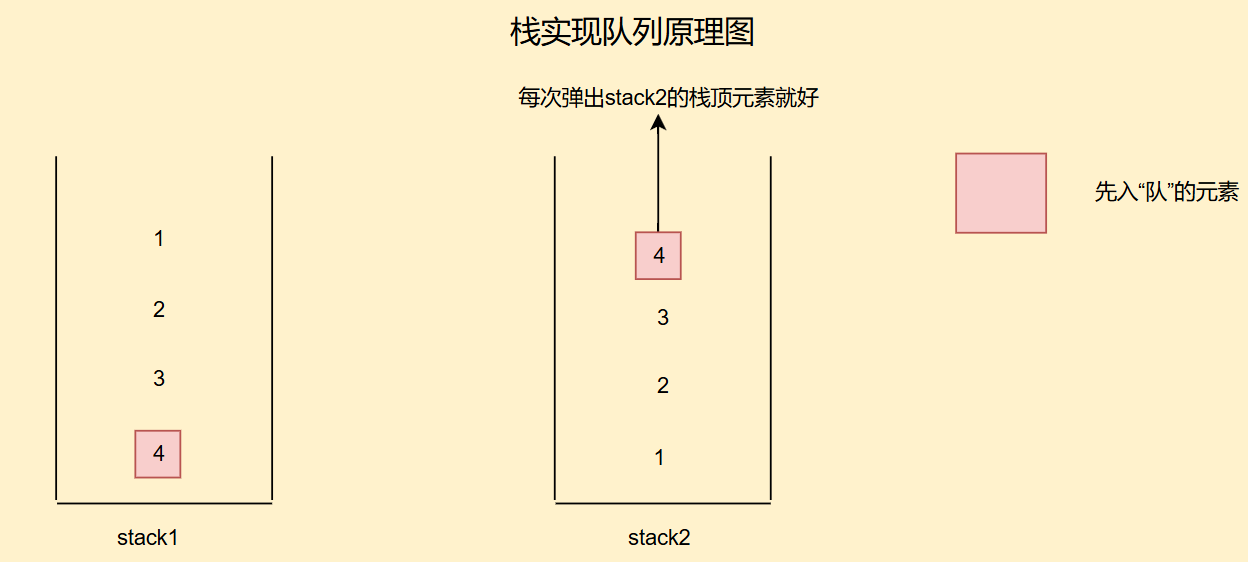
我們剛剛使用兩個隊列實現棧，那現在也要用兩個棧實現隊列
入隊我們默認放在第一個棧中，因為棧順序是先進后出的，因此我們再把第一個棧的元素放入第二個棧中，此時第二個棧的棧頂元素即出隊元素
如果第二個棧沒有數據，則先把第一個棧的所有元素拿過來

class MyQueue {private Stack<Integer> stack1;private Stack<Integer> stack2;public MyQueue() {stack1 = new Stack<>();stack2 = new Stack<>();}public void push(int x) {stack1.push(x);}public int pop() {if(empty()){return -1;}if(stack2.empty()){while(!stack1.empty()){stack2.push(stack1.pop());}}return stack2.pop();}public int peek() {if(empty()){return -1;}if(stack2.empty()){while(!stack1.empty()){stack2.push(stack1.pop());}}return stack2.peek();}public boolean empty() {return stack1.empty() && stack2.empty();}
}/*** Your MyQueue object will be instantiated and called as such:* MyQueue obj = new MyQueue();* obj.push(x);* int param_2 = obj.pop();* int param_3 = obj.peek();* boolean param_4 = obj.empty();*/

---

文章錯誤不可避免，期待您的指正，我們共同進步

---

---

END