目錄

一、初識線段樹

圖例：

?編輯

數組存儲：

指針存儲：

理由：

build函數建樹

二、線段樹的區間修改維護

區間修改維護：

區間修改的操作：

遞歸更新過程：

區間修改update：

三、線段樹的區間查詢

區間查詢：

區間查詢的操作：

遞歸查詢過程：

區間查詢query：

例題：

完整代碼：

數組實現：

指針實現：

總結

---

前言

今天我們來學習一下線段樹

模板題目：P3372 【模板】線段樹 1 - 洛谷

---

一、初識線段樹

首先我們來了解一下什么是線段樹

? ? ? 線段樹是一種數據結構，通常用來解決區間查詢的問題。它主要用于對一個包含有 n 個元素的數組進行區間操作，如查詢某個區間內的最大值、最小值、區間和等。

? ? ? ?線段樹的基本思想是將整個數組按照一定規則進行分割，每個節點代表一個區間。每個節點保存區間內的信息，如最大值、最小值、區間和等。父節點的信息可以通過子節點的信息合并得到，這樣就可以快速進行區間查詢。

? ? ? 線段樹通常是一棵完全二叉樹，葉子節點對應于數組中的元素，每個非葉子節點表示了其區間的信息。對于一個包含 n 個元素的數組，線段樹的節點數一般是 2n-1 或 2^k-1，其中 k 是大于等于 n 的最小整數。線段樹的構建包括建樹和更新兩個主要操作，查詢時可以通過遞歸的方式進行。

? ? ? ?線段樹在解決區間查詢問題時效率很高，時間復雜度一般為 O(logn)，其中 n 是數組元素個數。因此，線段樹被廣泛應用于需要頻繁進行區間查詢的場景，如動態區間最值查詢、區間和查詢等。

我這次是聯系模板題目P3372 【模板】線段樹 1 - 洛谷講解的最簡單的類型

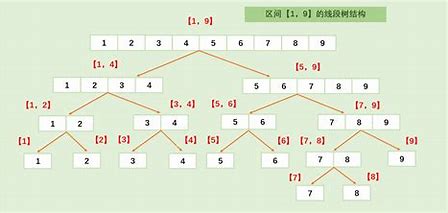
圖例：

? ? ? 通過這幅圖我們可以看出，線段樹是根據不斷的從子節點拿值，來更新父節點的值，直到得到整個區間的值，和分治的思想有點像，感覺

線段樹的存儲方式有兩種常見的實現方法：數組存儲和指針存儲。

1. 數組存儲：

   • 在數組存儲中，線段樹被表示為一個靜態的完全二叉樹。數組的下標從 1 開始，對于節點 i，其左子節點為 2i，右子節點為 2i+1。
   • 如果線段樹的葉子節點數量為 n，那么數組的大小一般取 4n，以確保足夠的空間。
   • 線段樹根節點一般存儲在數組下標為 1 的位置。
   • 通過按照規則在數組中存儲線段樹的節點，可以方便地進行查詢和更新操作。

2. 指針存儲：

   • 在指針存儲中，線段樹被表示為一個動態的樹結構，每個節點通過指針指向其左右子節點。
   • 每個節點通常由一個包含左右子節點指針的結構體或類表示。
   • 指針存儲方式在構建線段樹時會動態生成節點，相對于數組存儲來說更加靈活，但可能會消耗更多的內存空間。

? ? ?無論是數組存儲還是指針存儲，線段樹的基本操作都是相似的，包括建樹、查詢和更新。選擇適合具體應用場景的存儲方式可以更好地利用線段樹的優勢，提高算法效率。

? ? ? 首先是數組存儲，我們最先要知道的是數組的大小需要開多大，在線段樹的數組存儲中，通常會將數組的大小設置為 4n，其中 n 表示線段樹的葉子節點數量。

理由：

1. 完全二叉樹性質：線段樹一般是一棵完全二叉樹，具有規律性的結構。在數組存儲方式下，為了方便表示完全二叉樹，需要保證數組的大小是某一層節點數量的上限。對于一棵深度為 k 的完全二叉樹，葉子節點數量最多為 2^k，因此數組大小一般設置為 4 * 2^k，以確保足夠的空間。

2. 節點的父子關系：在數組存儲方式中，節點 i 的左子節點一般存儲在位置 2i，右子節點存儲在位置 2i+1。設置數組大小為 4n 可以保證對于任意節點 i，其子節點在數組中的位置都是有效的，不會越界。

3. 方便計算左右子樹位置：在線段樹的查詢和更新操作中，經常需要根據節點的索引快速定位其左右子樹節點。通過設置數組大小為 4n，可以方便地根據節點索引計算出其左右子節點的位置，簡化操作。

然后開一個build函數建樹，具體操作如下：

1. 定義數組：首先，需要定義一個大小為 4n 的數組，其中 n 是線段樹的葉子節點數量。這個數組將用于存儲線段樹的節點信息。

2. 構建線段樹：一般將線段樹按照完全二叉樹的形式存儲在數組中。假設根節點在數組中的索引是 1，那么對于節點 i，其左子節點為 2i，右子節點為 2i + 1。

3. 存儲節點信息：每個節點需要保存代表的區間范圍和相應的信息，比如區間的最大值、最小值、和等等。在數組中，可以按照某種順序依次存儲這些信息，以便后續的查詢和更新操作。

4. 建立線段樹：通過遞歸或迭代的方式構建線段樹。一般會從葉子節點開始向上構建，通過合并子節點的信息得到父節點的信息，直至構建完整的線段樹。

5. 查詢和更新：通過線段樹的結構和數組存儲，可以實現高效的區間查詢和更新操作。比如，對于查詢一個區間的最大值，可以通過遞歸向下查詢到包含目標區間的節點，并根據存儲的信息計算出結果。

6. 記得注意邊界情況：在實現線段樹時，需要考慮樹的邊界情況，比如樹的根節點索引是 1，葉子節點索引從 n+1 開始等，以確保正確地訪問和操作節點。

build函數建樹

void build(LL l, LL r, LL fa) {if (l == r) // //如果左右區間相同，那么必然是葉子節，只有葉子節點是被真實賦值的{t[fa] = a[l];return;}LL mid = (l + r) >> 1;build( l, mid, fa << 1);build(mid + 1, r, fa << 1 | 1);
//使用二分來優化psuh_up(fa);//此處由于我們是要通過子節點來維護父節點，所以push_up的位置應當是在回溯時將子節點的值取和交給父節點
}

二、線段樹的區間修改維護

? ? ? 線段樹是一種用于解決區間查詢和修改問題的數據結構。在線段樹中，區間修改維護指的是在給定一個區間，并修改該區間內所有元素的操作。

1. 區間修改維護：

   • 當需要修改線段樹中某個特定區間的值時，可以通過遞歸的方式向下更新區間。
   • 如果要修改的區間與當前節點表示的區間沒有交集，則無需修改該節點。
   • 如果要修改的區間完全包含當前節點的區間，則直接更新當前節點的信息，并將修改操作下傳給子節點。
   • 如果要修改的區間與當前節點的區間部分相交，則需要先將當前節點的信息更新，然后將修改操作同時下傳給左右子節點。

2. 區間修改的操作：

   • 區間修改的操作通常包括加法、減法、賦值等。
   • 當需要對區間內的每個元素進行相同的修改時，可以利用線段樹的特性進行高效操作。
   • 在修改區間時，需要根據當前節點的區間范圍、待修改區間和修改方式來確定如何操作當前節點和其子節點。

3. 遞歸更新過程：

   • 從線段樹的根節點開始遞歸向下更新，直到找到包含待修改區間的葉子節點。
   • 在遞歸過程中根據節點的區間范圍和待修改區間的關系，決定如何更新節點的信息并向下傳遞修改操作。

? ? ? ?此外，對于區間操作，我們考慮引入一個名叫“?lazy?tag?”（懶標記）的東西——之所以稱其“lazy”，是因為原本區間修改需要通過先改變葉子節點的值，然后不斷地向上遞歸修改祖先節點直至到達根節點，時間復雜度最高可以到達?O(nlogn)?的級別。但當我們引入了懶標記之后，區間更新的期望復雜度就降到了?O(logn)?的級別且甚至會更低。

因此，我們再弄一個tag數組，大小也是4*N

區間修改update：

void psuh_up(LL fa) {t[fa] = t[fa << 1] + t[fa << 1 | 1];//向上不斷維護父節點
}
void push_down(LL l,LL r,LL fa) {LL mid = (l + r) >> 1;t[fa << 1] += tag[fa] * (mid - l + 1);tag[fa << 1] += tag[fa];t[fa << 1|1] += tag[fa] * (r-mid);tag[fa << 1|1] += tag[fa];tag[fa] = 0;// //每次將懶惰標識下放到兩個兒子節點，自身置為0，以此不斷向下傳遞 
}
void update(LL ql, LL qr, LL l, LL r, LL k, LL fa) {if (ql <= l && qr >= r) //如果區間被包含，直接返回該節點的懶惰標識{t[fa] +=k * (r - l + 1);tag[fa] += k;return;}LL mid = (l + r) >> 1;push_down(l, r, fa);//下放懶惰標識if (ql <= mid)update(ql, qr, l, mid,k, fa << 1);//朝左邊下放if (qr > mid)update(ql, qr, mid + 1, r,k, fa << 1 | 1);//右邊psuh_up(fa);//再將修改后的值向上返回，維護父節點
}

三、線段樹的區間查詢

1. 區間查詢：

   • 當需要查詢線段樹中某個特定區間的信息時，可以通過遞歸的方式向下查詢區間。
   • 如果要查詢的區間與當前節點表示的區間沒有交集，則無需查詢該節點，直接返回默認值（如0或無窮大）。
   • 如果要查詢的區間完全包含當前節點的區間，則直接返回該節點存儲的信息。
   • 如果要查詢的區間與當前節點的區間部分相交，則需要同時查詢左右子節點，并根據查詢結果合并得到最終結果。

2. 區間查詢的操作：

   • 區間查詢的操作通常包括求和、求最大值、求最小值等。
   • 在查詢區間時，需要根據當前節點的區間范圍、待查詢區間和查詢方式來確定如何操作當前節點和其子節點。

3. 遞歸查詢過程：

   • 從線段樹的根節點開始遞歸向下查詢，直到找到包含待查詢區間的葉子節點。
   • 在遞歸過程中根據節點的區間范圍和待查詢區間的關系，決定如何查詢節點的信息并向下傳遞查詢操作。
   • 最終將所有查詢結果合并得到最終的區間查詢結果。

? ? ? 通過以上方法，可以實現對線段樹中特定區間的查詢操作。線段樹區間查詢是線段樹的一個重要功能，能夠快速有效地獲取區間內的信息，提高了區間查詢的效率。

區間查詢query：

LL query(LL ql, LL qr, LL l, LL r, LL fa) {LL ret = 0;if (ql <= l && qr >= r) 如果區間被包含，直接返回該節點的懶惰標識{return t[fa];}LL mid = (l + r) >> 1;push_down(l, r, fa);//沒有被包含，下放任務if (ql <= mid)ret += query(ql, qr, l, mid, fa << 1);if (qr > mid)ret += query(ql, qr, mid + 1, r, fa << 1|1);//在查詢范圍的左區間和右區間的值相加并返回return ret;
}

例題：

模板題目：P3372 【模板】線段樹 1 - 洛谷

完整代碼：

數組實現：

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
LL n, m, t[N * 4], tag[N * 4], a[N];
void psuh_up(LL fa) {t[fa] = t[fa << 1] + t[fa << 1 | 1];//向上不斷維護父節點
}
void push_down(LL l,LL r,LL fa) {LL mid = (l + r) >> 1;t[fa << 1] += tag[fa] * (mid - l + 1);tag[fa << 1] += tag[fa];t[fa << 1|1] += tag[fa] * (r-mid);tag[fa << 1|1] += tag[fa];tag[fa] = 0;// //每次將懶惰標識下放到兩個兒子節點，自身置為0，以此不斷向下傳遞 
}
LL query(LL ql, LL qr, LL l, LL r, LL fa) {LL ret = 0;if (ql <= l && qr >= r) 如果區間被包含，直接返回該節點的懶惰標識{return t[fa];}LL mid = (l + r) >> 1;push_down(l, r, fa);//沒有被包含，下放任務if (ql <= mid)ret += query(ql, qr, l, mid, fa << 1);if (qr > mid)ret += query(ql, qr, mid + 1, r, fa << 1|1);//在查詢范圍的左區間和右區間的值相加并返回return ret;
}
void update(LL ql, LL qr, LL l, LL r, LL k, LL fa) {if (ql <= l && qr >= r) //如果區間被包含，更新懶惰標識并返回{t[fa] +=k * (r - l + 1);tag[fa] += k;return;}LL mid = (l + r) >> 1;push_down(l, r, fa);//下放懶惰標識if (ql <= mid)update(ql, qr, l, mid,k, fa << 1);//朝左邊下放if (qr > mid)update(ql, qr, mid + 1, r,k, fa << 1 | 1);//右邊psuh_up(fa);//再將修改后的值向上返回，維護父節點
}
void build(LL l, LL r, LL fa) {if (l == r) // //如果左右區間相同，那么必然是葉子節，只有葉子節點是被真實賦值的{t[fa] = a[l];return;}LL mid = (l + r) >> 1;build(l, mid, fa << 1);build(mid + 1, r, fa << 1 | 1);//使用二分來優化psuh_up(fa);//此處由于我們是要通過子節點來維護父節點，所以push_up的位置應當是在回溯時將子節點的值取和交給父節點
}
int main() {cin >> n >> m;for (int i = 1; i <= n; i++)cin >> a[i];build(1, n, 1);while (m--) {int op; cin >> op;if (op == 1) {LL x, y, k; cin >> x >> y >> k;update(x, y, 1, n, k, 1);}else if(op==2){LL x, y;cin >> x >> y;cout << query(x, y, 1, n, 1) << endl;}}return 0;
}

指針實現：

#include <iostream>
#include <vector>using namespace std;struct Node {int start, end;int sum;Node *left, *right;Node(int start, int end) : start(start), end(end), sum(0), left(nullptr), right(nullptr) {}
};Node* buildSegmentTree(vector<int>& nums, int start, int end) {if (start > end) {return nullptr;}Node* root = new Node(start, end);if (start == end) {root->sum = nums[start];} else {int mid = start + (end - start) / 2;root->left = buildSegmentTree(nums, start, mid);root->right = buildSegmentTree(nums, mid + 1, end);root->sum = root->left->sum + root->right->sum;}return root;
}int query(Node* root, int qs, int qe) {if (root == nullptr || qs > root->end || qe < root->start) {return 0;} else if (qs <= root->start && qe >= root->end) {return root->sum;} else {return query(root->left, qs, qe) + query(root->right, qs, qe);}
}int main() {vector<int> nums = {1, 3, 5, 7, 9, 11};Node* root = buildSegmentTree(nums, 0, nums.size() - 1);cout << "Sum of elements in range [2, 4]: " << query(root, 2, 4) << endl;return 0;
}

---

總結

本文關于線段樹的講解就到這里，有什么疑問或者有什么錯誤的地方歡迎一起交流學習