一、文獻閱讀

題目信息

• 題目： Application of a semivariogram based on a deep neural network to Ordinary Kriging interpolation of elevation data
• 期刊： PLOS ONE
• 作者： Yang Li, Zhong Baorong, Xu Xiaohong, Liang Zijun
• 發表時間： 2022
• 文章鏈接： https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0266942

摘要

普通克里金是常用的空間插值方法，其半變異函數的擬合效果對插值精度有顯著影響。常用的半變異函數模型有高斯、球形和指數模型，一般需手動比較和調整參數來選擇最優模型。現有的半變異函數擬合方法存在手動分析選擇模型和受所選模型限制的問題。為減少手動選擇模型的繁瑣過程，提高擬合優度，本文提出用DNN模擬半變異函數進行插值。本文提出了一種基于深度神經網絡和普通克里金的空間插值新方法。通過Python的Keras建立DNN模型擬合半變異函數，以高程數據為案例研究。將該方法的插值結果與傳統的指數、高斯和球形模型進行對比，結果表明基于DNN的方法克里金方差更小，插值結果更接近理論值，還能簡化半變異函數分析過程。這解決了傳統半變異函數擬合的問題，提高了插值精度，簡化了分析過程，對地理統計和空間插值領域有重要意義。

創新點

提出用DNN模擬半變異函數進行OK插值，理論上可擬合所有函數，能獲得最佳擬合的半變異函數，提高插值精度。

實驗

將深度神經網絡與普通克里金法相結合，這個模型的選擇和擬合效果直接影響最終插值的精度。實驗選取了四個獨立的 50x50 區域（4個區域）作為高程數據測試區 。
實驗可分為半變異函數擬合、普通克里金插值 和 結果對比分析三個階段

一、半變異函數擬合

研究對比了三種模型的擬合效果：DNN 模型、高斯模型和指數模型。
DNN 模型構建：使用基于 Python 的 TensorFlow 和 Keras 庫來搭建 DNN 模型。設置了 15 個全連接層。輸入層和輸出層的神經元數量均為 1 。中間隱藏層使用 Relu 激活函數，以加快神經元擬合速度；輸入和輸出層則使用 Softplus 函數；優化器選擇 Adam，因為它訓練時間短且效果好。損失函數為均方誤差。
半變異函數遵循地理學第一定律約束。在訓練過程中監控模型的梯度，一旦出現負梯度，就選擇上一步訓練得到的全正梯度模型，以確保函數單調遞增 。驗證采用了 k-折交叉驗證（k=10）。將用于擬合的數據集分成 10 份，每次用 9 份作為訓練集，1 份作為驗證集，共進行 10 次訓練，以優化模型權重。對于高斯模型和指數模型，研究使用了最小二乘法來擬合 80% 的數據點 。

二、普通克里金插值

無論是使用 DNN 還是傳統模型得到的半變異函數，后續的普通克里金插值流程是統一的：

1. 、將未知點與已知樣本點之間的距離代入已擬合好的半變異函數模型（DNN 模型、高斯模型或指數模型），得到它們之間的半變異函數值 。
2. 利用得到的半變異函數值構建克里金方程組，求解得到每個已知樣本點對于未知點的權重系數 λ。
3. 通過加權求和的方式，計算出未知點的估算值 。
4. 對所有待插值的點重復以上步驟

三、結果對比分析

為了全面評估 DNN-OK 方法的性能，研究設置了多個評估指標，并與高斯-OK和指數-OK進行對比。
在進行克里金插值前，對四個區域的樣本集進行了柯爾莫哥洛夫-斯米爾諾夫檢驗（Kolmogorov-Smirnov test），計算 P-value。結果顯示所有區域的 P-value 均大于 0.05，表明樣本服從正態分布，適合進行 OK 插值 。

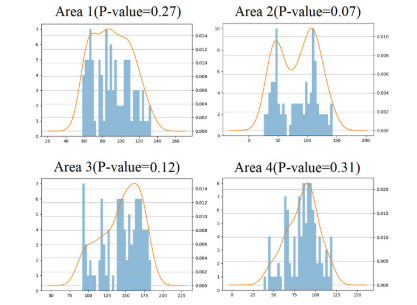
四、實驗結果

擬合效果：
使用決定系數 $R^2$ 來評估各個模型對半變異函數的擬合效果。$R^2$ 越接近 1，說明模型的擬合效果越好。分別在訓練集（80%）和測試集（20%）上計算了 $R^2$ 值 。
在訓練集上，DNN 模型的 $R^2$ 值在所有四個區域中均顯著高于高斯和指數模型，達到了 0.98 以上。在測試集上，DNN 模型的泛化能力同樣表現出色，其 $R^2$ 值也普遍優于傳統模型。這表明 DNN 能夠更精確地捕捉數據的空間相關性結構。

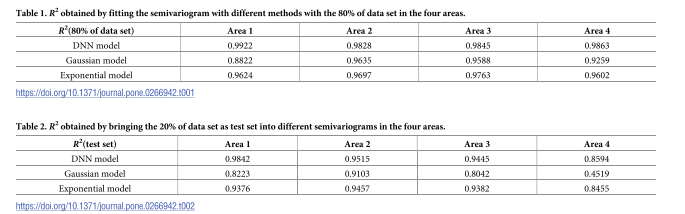
克里金方差：
該指標衡量插值結果與理論結果的偏離程度。克里金方差越小，說明插值結果越接近理論上的最優估計 。DNN-OK 方法在所有四個區域產生的平均克里金方差都是最小的。例如，在區域 1，DNN-OK 的方差為 52.52，而高斯-OK 和指數-OK 分別為 90.87 和 92.42 。這證明了 DNN-OK 的結果在理論上更穩定，更接近最優無偏估計。

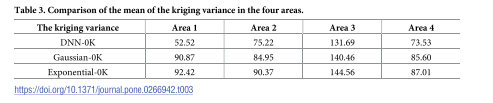
插值精度：
通過將插值結果與原始數據的真實值進行比較，計算 MAE 和 RMSE，這兩個值越小，代表插值精度越高。DNN-OK 在四個區域中的三個區域的 MAE 值均低于其他兩種方法；DNN-OK 在所有四個區域的 RMSE 值幾乎都取得了最好或次好的結果，顯著改善了插值精度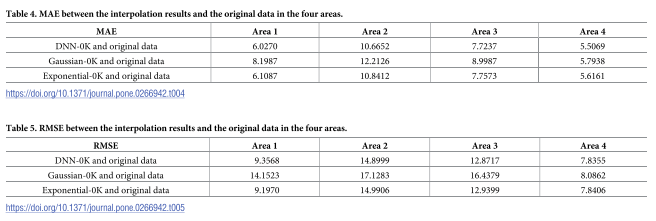

結論

DNN能擬合出最優半變異函數，反映最佳空間相關性，可替代多數其他半變異函數，簡化分析過程；該方法使克里金方差最小，優化了OK算法；雖需更多計算時間，但可節省人工分析時間。

不足以及展望

基于DNN擬合的半變異函數需要更多計算時間，對GPU性能要求較高。可進一步優化DNN模型，減少計算時間。