📝前言說明：

• 本專欄主要記錄本人的基礎算法學習以及LeetCode刷題記錄，按專題劃分
• 每題主要記錄：（1）本人解法 + 本人屎山代碼；（2）優質解法 + 優質代碼；（3）精益求精，更好的解法和獨特的思想（如果有的話）
• 文章中的理解僅為個人理解。如有錯誤，感謝糾錯

🎬個人簡介：努力學習ing
📋本專欄：C++刷題專欄
📋其他專欄：C語言入門基礎，python入門基礎，C++學習筆記，Linux
🎀CSDN主頁 愚潤澤

---

202. 快樂數

個人解

思路：沒思路，不知道如何判斷這個數不是快樂樹
用時：13:00
屎山代碼：無

---

優質解：

思路：不要偷懶，自己手算一遍這個過程才能發現規律

你要問我為什么一定能成環？
題目所給的數字范圍：1 <= n <= 2^31 - 1，2^31 - 1 == 2,147,483,647，總共有9位數，我們往大了取，假設每一位都為9，則999999999的平方和肯定是最大的，結果是9*9*10 == 810，那最小的數呢？顯然是1，也就是說每次變化的取值是在[1, 810]里面取。
但是，無限循環，取無數次，在[1, 810]里面取無數次，必然有重復！

對于能變成1的快樂數，因為1的平方還是1，所以，最后也是在一個全是1的環內循環

所以，這道題就變成：可以用快慢指針，慢指針每次移動一步，快指針每次移動兩步，因為有速度差且有環，所以快慢指針一定會在環內相遇。當快慢指針相遇時，判斷相遇的數是否為1即可。

代碼：

class Solution {
public:int Sum(int n){int sum = 0;while(n){int i = n % 10;sum += i * i;n /= 10;}return sum;}bool isHappy(int n) {int slow = n, fast = Sum(n); // 這里可不能 fast == n, 因為while的判斷條件是slow == fastwhile(slow != fast){slow = Sum(slow);fast = Sum(Sum(fast));}return slow == 1;}
};

---

11 盛最多水的容器

個人解

思路：

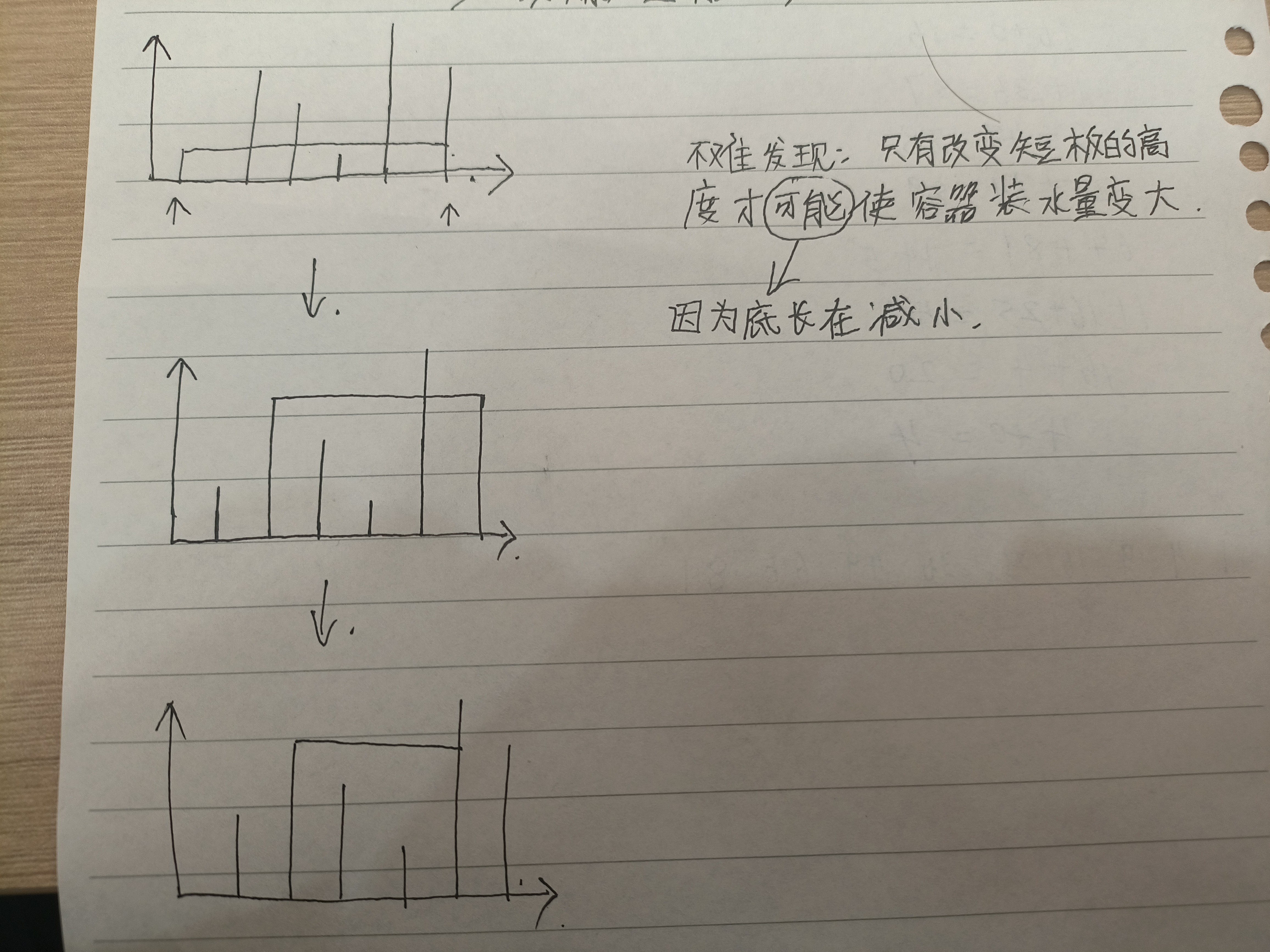
每次讓短的邊移動。
移動完成后，重新計算容積V的大小，如果更大就替換

用時：10:00（通過，因為這題以前寫過）
屎山代碼：

class Solution {
public:int maxArea(vector<int>& height) {int ans = 0, left = 0, right = height.size() - 1;while(left < right){int v = min(height[left], height[right]) * (right - left);if(v > ans) ans = v;else{if(height[left] < height[right]){left++;}else{right--;}}}return ans;}
};

時間復雜度：O(n)
空間復雜度：O(1)

---

優質解：

個人解已經比較優秀的解法了，不再過多探索

---

611. 有效三角形的個數

個人解

思路：通過枚舉 最大邊 + 相向指針 求解。

1. 先對數組進行排序，整個數組遞增
2. 枚舉最大邊cur，然后設置雙指針：right = cur - 1，left = 0
3. 要滿足可以形成三角形，就需要兩個短邊之和 > 最大邊
4. 又因為數組有遞增性，如果當前的left,right,cur所指向的三個數可以形成三角形，則right和left到right之間的所有數組合也可以形成三角形，因為這些值>=left指向的值。
5. 雙指針的移動問題，要滿足nums[left] + nums[right] > nums[cur]，很明顯：left左移，會讓左式更大，right右移會讓左式更小。所以當不滿足條件的時候，left左移，當滿足條件以后right右移。

但是，我在做題的時候一開始嘗試 枚舉最小邊 + 相向指針 出現了問題：如果我枚舉的是最小邊，則要滿足：nums[right] - nums[left] < nums[cur]，這時候因為數組是遞增的，就出現了問題。因為right左移，左式會變小，left右移左式也會變小，變化相同顯然是行不通的。

用時：18:00
屎山代碼（通過）：

class Solution {
public:int triangleNumber(vector<int>& nums) {int ans = 0, n = nums.size();ranges::sort(nums); // ranges 是 C++20 引入的ranges庫for(int cur = n - 1; cur > 1; cur--) // 枚舉最長邊{int left = 0, right = cur - 1;while(left < right){if(nums[left] + nums[right] > nums[cur]){ans += right - left;right--;}else{left++;}}}return ans;}
};

時間復雜度：O($n^2$)
空間復雜度：O(1)

---

優質解：

枚舉最小邊的處理方法：
用同向雙指針（滑動窗口）。
當left和right的指針越靠近的時候，兩邊的差值越小。
我們可以，一開始讓right和left足夠接近，讓[left, right]這個窗口里面的組合都滿足nums[right] - nums[left] < nums[cur]，即：可以構成三角形
如何實現呢？
只需要在滿足nums[right] - nums[left] < nums[cur]的時候，讓left右移，移動到第一個滿足的地方就停下來，然后統計窗口內滿足的個數，加入ans。一組算完以后，讓right右移變遠，但是left無須倒退，因為right增大了，左式增大，這時候要找的是讓左式更小的left（這個很關鍵，不然容易寫成O($n^3$)，我就是，進行了回退…），進行下一組的計算。

代碼：

class Solution {
public:int triangleNumber(vector<int>& nums) {int ans = 0, n = nums.size();ranges::sort(nums); // ranges 是 C++20 引入的ranges庫for(int cur = 0 ; cur < n - 2; cur++) // 枚舉最短邊{int left = cur + 1;for(int right = cur + 2; right < n; right++){while(left < right && nums[right] - nums[left] >= nums[cur]){left++;}ans += right - left;}}return ans;}
};

時間復雜度：O($n^2$)
空間復雜度：O(1)

---

🌈我的分享也就到此結束啦🌈
要是我的分享也能對你的學習起到幫助，那簡直是太酷啦！
若有不足，還請大家多多指正，我們一起學習交流！
📢公主，王子：點贊👍→收藏?→關注🔍
感謝大家的觀看和支持！祝大家都能得償所愿，天天開心！！！