算法系列七：歸并排序

一、歸并排序的遞歸探尋

1.思路

2.搭建

2.1設計過掉不符情況（在最底層時）

2.2查驗能實現基礎排序（在最底層往上點時）

2.3跳轉結果繼續往上回搭

3.實質

4.實現

二、遞歸的調用棧

1.遞歸的執行過程

2.遞歸的函數棧幀

2.1遞歸函數的棧幀壓彈

2.2合并有序數組函數的棧幀壓彈

三、歸并排序的復雜度

1.空間復雜度

2.時間復雜度

---

一、歸并排序的遞歸探尋

1.思路

理想結果等于成分解斷開子結果表達式的公式表示

快速排序：

整個數組有序 = 其中一個元素有序 + 其左斷開數組有序 + 其右斷開數組有序

歸并排序：

整個數組有序 = 左斷開數組有序 + 右斷開數組有序 + 兩有序數組的有序合并

---

2.搭建

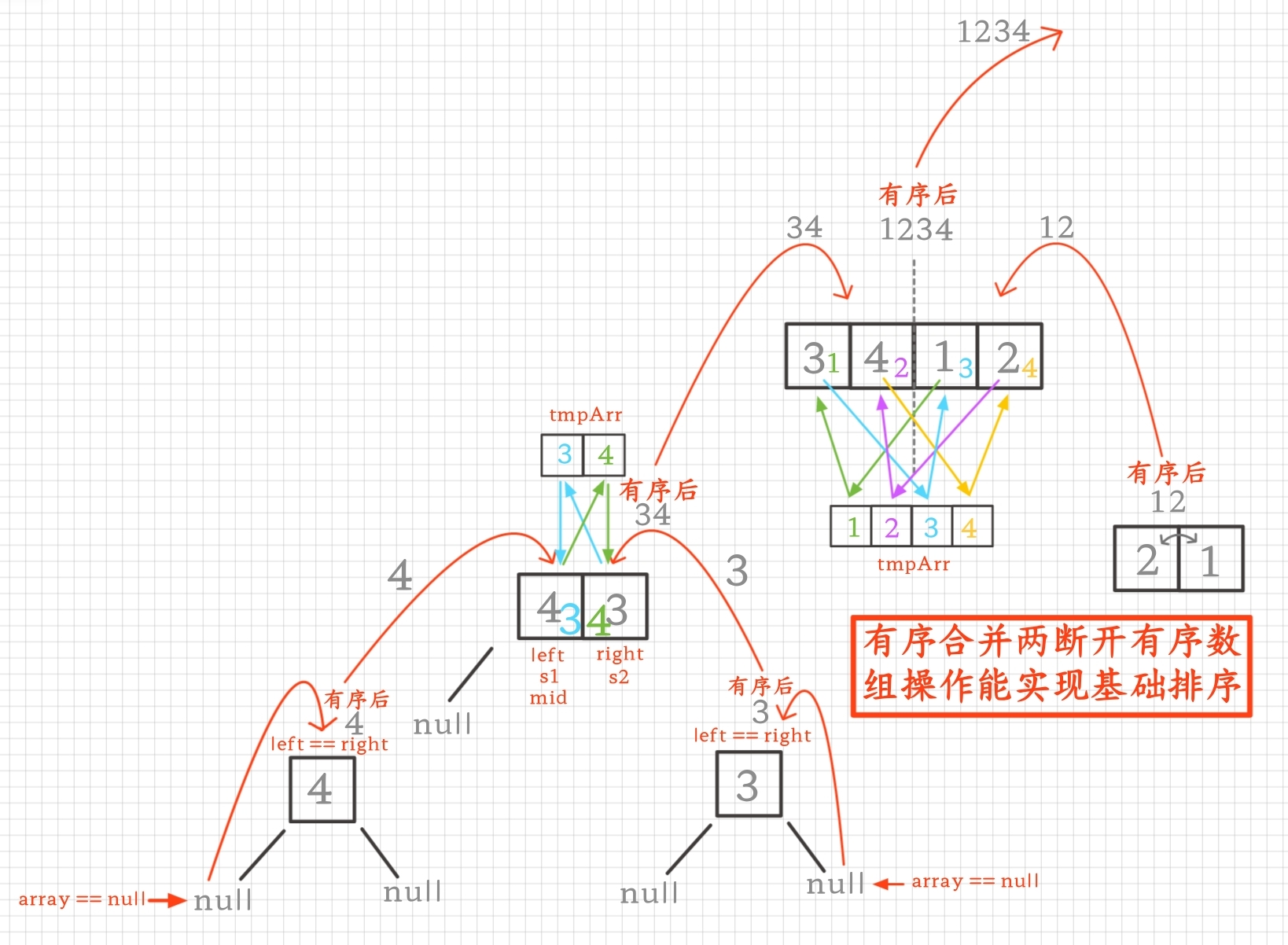
2.1設計過掉不符情況（在最底層時）

• if(array == null) return， 數組沒有元素不用排，下面是有元素
• if(left == right) return，只有一個元素已經是有序了不用排，下面是多個元素
• if(left > right) return，排不了不要排的，之后下面是符合一般情況的多個元素?

---

2.2查驗能實現基礎排序（在最底層往上點時）

在最底層往上點時，有序數組有序合并操作在最底層能實現兩元素之間的比較然后進行排序的

---

2.3跳轉結果繼續往上回搭：

跳轉有序數組結果繼續往上有序合并維護回搭

---

3.實質

從底層的最小單個斷開有序數組往上有序地合并成越來越大的斷開有序數組直至合并完成一個整體的有序數組

---

4.實現

    public static void mergeSort(int[] array) {mergeSortFunc(array,0,array.length-1);}private static void mergeSortFunc(int[] array,int left,int right) {if(left >= right) return;int mid = (left+right) / 2;mergeSortFunc(array,left,mid);mergeSortFunc(array,mid+1,right);merge(array,left,right,mid);}private static void merge(int[] array, int left, int right, int mid) {int s1 = left;int s2 = mid+1;int[] tmpArr = new int[right-left+1];int k = 0;//證明兩個區間 都同時有數據的while (s1 <= mid && s2 <= right) {if(array[s2] <= array[s1]) {tmpArr[k++] = array[s2++];}else {tmpArr[k++] = array[s1++];}}while (s1 <= mid) {tmpArr[k++] = array[s1++];}while (s2 <= right) {tmpArr[k++] = array[s2++];}//tmpArr 里面一定是這個區間內有序的數據了for (int i = 0; i < tmpArr.length; i++) {array[i+left] = tmpArr[i];}}

---

二、遞歸的調用棧

1.遞歸的執行過程

在函數遞歸中，調用的函數里面執行著再調用著隨著形參深入的不斷變化的函數自己：

第一次調用函數的執行轉去等著第二次調用函數的執行完，第二次調用函數的執行也卡著轉去等第三次調用函數的執行完，一層層形參變化著重復地執行調用而都沒有往下去return，直到最后調用函數傳的形參變化到符合return的條件不再繼續往下調用了，return出結果開始往回地一層層促進上一層沒有執行完到執行完return，即開始往回地執行往回地歸

---

2.遞歸的函數棧幀

所有任意一個函數的調用都會獨立開辟新的函數棧幀(里面存放局部變量、函數形參、返回地址、寄存器值）壓入調用棧中，在函數執行到return語句結束后才彈出棧：

遞歸調用時，函數棧幀從先往后地一個個獨立地壓入棧中，往下遞歸直到形參條件變到return后由最新函數調用的棧幀開始往上彈棧幀出調用棧，在開始往上彈出棧幀開始有執行完往回層往下執行時，方法里面有可能寫的是繼續又去執行調用當前層形參條件下的再來一波函數遞歸調用(形參變化可能就去設置成不同的了就會是左右不一樣的分支)，即是二叉即二叉樹的情況：

• 每一層不僅要左邊往下全執行到底層然后開始往上全執行到它那層的左邊結束，接著又要執行右邊的往下執行到底層然后再往上全執行完到它的右層結束，最后它這個節點對應的這層函數才也執行完它的棧幀也彈出調用棧，二叉樹從大到小所有的結構都是左邊往下全執行完往上回來、右邊往下全執行完往上回來、接著它這個節點的棧幀也往上彈返回執行完?

---

2.1遞歸函數的棧幀壓彈

在歸并排序的二叉樹遞歸調用過程中：

1. 每次累計著往下調用到底層時，此時的調用棧所占的空間是最大的、深度在二叉樹的最底層，調用棧的空間計算為調用棧里棧幀的個數×每個棧幀的內存大小，在每個函數的棧幀中，函數里面那些函數的調用信息、并非循環出現的常量個數的局部變量空間和都可算成常數的大小，所以在歸并排序這里，調用棧的最大空間為在調用棧里棧幀個數最多的時候：樹的高度log(n)*每個函數棧幀的內存大小是常數，即log(n)*常數，函數調用執行完最底層后就開始有往上返回了，往上彈出最新最頂的棧幀
2. 然后執行完返回到上層時又回到當前層條件下的且新的形參變化模式的再往下遞歸，又會去壓棧到最底層，此時調用棧的空間又達到最大的log(n)
3. 當它右邊往下的也全執行完又往上返回到當前層時，就開始繼續往下接著執行就開始有去調用合并有序數組的函數了

---

2.2合并有序數組函數的棧幀壓彈

執行調用合并有序數列的函數時，調用棧又會壓入合并有序數組函數的棧幀，里面存放有開辟的當前層數組元素個數大小的數組(非常量級的，要算的)，此時總的占用空間為調用棧的空間log(n-...)+n(-...)，因為合并有序數組函數的棧幀每次都是處在棧頂壓入的且函數里面并沒有再調用函數的在它之上再壓棧，所以它每次在棧頂進來壓棧完就緊接著彈出棧的

---

三、歸并排序的復雜度

1.空間復雜度

空間復雜度計算的是整個執行所有時刻中出現的最大瞬時占用空間：

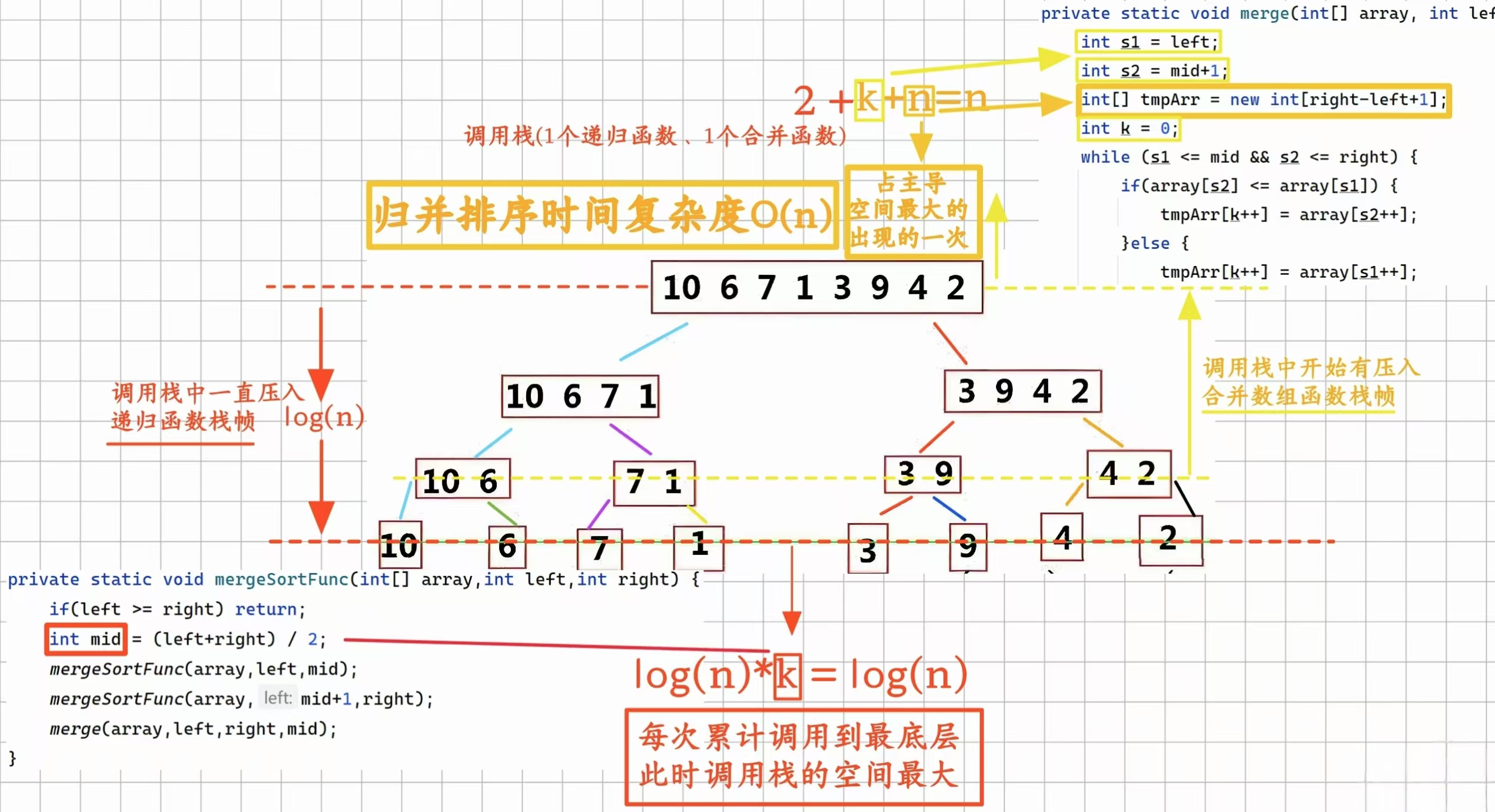
從下層往上層的返回的過程中，遞歸函數的調用棧空間變小著、合并有序數組的函數棧幀在變大著(里面的數組越來越大的)：

• 在最底層時占用的空間為遞歸函數的調用棧空間log(n)+合并有序數組的函數棧幀0，即log(n)+0=log(n)
• 當到達最上層第一層時，遞歸函數的調用棧空間是1，而合并有序數組的函數棧幀空間是n，此時的總空間大小是n，相比于最底層的log(n)及從下往上的過程中log(n)的遞減、n的遞增的總空間，此時的n是整個執行所有時刻中出現的最大瞬時占用的空間，所以歸并排序的空間復雜度是O(n)

---

2.時間復雜度

時間復雜度即算整個遞歸調用執行過程的時間和，我們可以不用按著遞歸搜索的過程去時時累計總的算，直接站在總二叉樹的角度一層一層地算所有時間的和就行了，一層層里面每一個樹節點及下的全執行完對應著該調用函數的全執行完，因為遞歸調用語句mergeSortFunc(array,left,mid)都是且已轉成里面的函數節點內容來算了(調用中的去執行調用部分是常量級的已不算)，且if(left >= right) return、int mid = (left+right) / 2也都是常量級的執行時間不算，對應到總的時間就是計算所有函數節點里的merge(array,left,right,mid)合并有序數組的時間和，每一層所有函數節點的合并有序數組時間和都為n(除了最后一層的函數節點進去就直接判斷為return沒執行有序數組合并)，一共有log(n)層，所以時間復雜度為O(n*log(n))?