機器學習中的距離度量與優化方法：從曼哈頓距離到梯度下降

前言
一、曼哈頓距離(Manhattan Distance)：
二、切比雪夫距離 (Chebyshev Distance)：
三、閔可夫斯基距離(Minkowski Distance)：
小結
四、余弦距離(Cosine Distance)
五、杰卡德距離(Jaccard Distance)
六、交叉驗證方法
6.1 HoldOut Cross-validation（Train-Test Split）（保留交叉驗證）
6.2 K-折交叉驗證（K-fold Cross Validation，記為K-CV）
七、前向傳播與損失函數反向傳播的學習率與梯度下降
7.1 求導法則
7.1.1 導數含義
7.1.1.1舉例子理解
例1：速度(小車在馬路上勻速的前進)：
例2：速度(小車在馬路上非勻速的前進)：
7.2 什么是導數
7.3 常見的導數
7.3.1線性函數的導數：
7.3.2 其它常見的導數：
7.2 不可微函數
7.4 導數的求導法則
7.4.1 導數求導法則的定義：
7.4.2 兩個函數相加的導數
7.4.3 兩個函數乘積的導數
7.4.4 兩個函數的比值的導數
7.5 復合求導運算：
7.6 鏈式求導法則：
7.7 偏導數
7.7.1 偏導數定義
7.8 梯度
八、前向傳播與損失函數
8.1 前向傳播與損失函數理論講解
?8.1.1 前向傳播的定義
8.1.2 前向傳播的過程
8.1.3 前向傳播的作用
8.1.4 損失函數的概念：
8.2 基礎原理講解
8.2.1 案例導入
8.2.2 前向計算
8.2.3 單點誤差
8.2.4 損失函數：均方差
總結

前言

書接上文

KNN算法深度解析：從決策邊界可視化到鳶尾花分類實戰-CSDN博客文章瀏覽閱讀660次，點贊11次，收藏10次。本文系統講解了KNN算法的決策邊界形成機制、Scikit-learn實現細節及鳶尾花分類實戰，涵蓋K值選擇對邊界的影響、API參數解析、數據預處理（歸一化/標準化）和數據集劃分方法，通過代碼示例和可視化分析幫助讀者掌握KNN的核心應用技巧。https://blog.csdn.net/qq_58364361/article/details/147201792?spm=1011.2415.3001.10575&sharefrom=mp_manage_link

一、曼哈頓距離(Manhattan Distance)：

定義：曼哈頓距離是計算兩點之間水平線段或垂直線段的距離之和，也稱為城市街區距離或L1距離

eg:

在曼哈頓街區要從一個十字路口開車到另一個十字路口，駕駛距離顯然不是兩點間的直線距離。這個實際駕駛距離就是“曼哈頓距離”。曼哈頓距離也稱為“城市街區距離”(City Block distance)。

距離公式：

缺點：由于它不是可能的最短路徑，它比歐幾里得距離更有可能給出一個更高的距離值，隨著數據維度的增加，曼合頓距離的用處也就越小。

#曼哈頓距離
import numpy as np#計算曼哈頓距離
x = [1, 2]  # 點x的坐標
y = [3, 4]  # 點y的坐標#法一：使用循環計算曼哈頓距離
def manhattan_distance(x, y):"""計算兩個點之間的曼哈頓距離參數:x (list): 第一個點的坐標列表y (list): 第二個點的坐標列表返回:int/float: 兩個點之間的曼哈頓距離"""sum = 0for a, b in zip(x, y):sum += abs(a - b)return summd = manhattan_distance(x, y)  # 調用函數計算曼哈頓距離
print(md)  # 輸出結果#法二：使用numpy計算曼哈頓距離
def manhattan_distance2(x, y):"""使用numpy計算兩個點之間的曼哈頓距離參數:x (list): 第一個點的坐標列表y (list): 第二個點的坐標列表返回:int/float: 兩個點之間的曼哈頓距離"""x_1 = np.array(x)  # 將列表轉換為numpy數組y_1 = np.array(y)  # 將列表轉換為numpy數組return np.sum(np.abs(x_1 - y_1))  # 使用numpy函數計算絕對差的和md2 = manhattan_distance2(x, y)  # 調用函數計算曼哈頓距離
print(md2)  # 輸出結果

D:\python_huanjing\.venv1\Scripts\python.exe C:\Users\98317\PycharmProjects\study_python\機器學習\day4_15.py 
4
4進程已結束，退出代碼為 0

二、切比雪夫距離 (Chebyshev Distance)：

定義：切比雪夫距離是計算兩點在各個坐標上的差的絕對值的最大值。

國際象棋中，國王可以直行、橫行、斜行，所以國王走一步可以移動到相鄰8個方格中的任意一個。國王從格子(x1,y1)走到格子(x2,y2)最少需要多少步？這個距離就叫切比雪夫距離。

缺點：切比雪夫距離通常用于非常特定的用例，這使得它很難像歐氏距離那樣作通用的距離度量

#切比雪夫距離
import numpy as np#計算切比雪夫距離
x = [1, 2]  # 第一個點的坐標
y = [4, 6]  # 第二個點的坐標#第一種方式計算切比雪夫距離
def chebyshev_distance(x, y):"""計算兩個點之間的切比雪夫距離（使用純Python實現）參數:x (list): 第一個點的坐標列表y (list): 第二個點的坐標列表返回:float: 兩個點之間的切比雪夫距離"""max_list = []for a, b in zip(x, y):max_list.append(abs(a - b))return max(max_list)cd = chebyshev_distance(x, y)
print(f"cd:{cd}")#第2種方法
def chebyshev_distance1(x, y):"""計算兩個點之間的切比雪夫距離（使用NumPy實現）參數:x (list): 第一個點的坐標列表y (list): 第二個點的坐標列表返回:float: 兩個點之間的切比雪夫距離"""x_1 = np.array(x)y_1 = np.array(y)return np.max(np.abs(x_1 - y_1))cd1 = chebyshev_distance1(x, y)
print(f"cd1 :{cd1}")

D:\python_huanjing\.venv1\Scripts\python.exe C:\Users\98317\PycharmProjects\study_python\機器學習\day4_15.py 
cd:4
cd1 :4進程已結束，退出代碼為 0

三、閔可夫斯基距離(Minkowski Distance)：

兩個n維變量a(x11,x12,…,x1n)與b(x21,x22,…,x2n)間的閔可夫斯基距離定義為：

其中p是一個變參數：

當p=1時，就是曼哈頓距離；

當p=2時，就是歐氏距離；

當p→∞時，就是切比雪夫距離。

根據p的不同，閔氏距離可以表示某一類/種的距離。

import numpy as npx = [1, 2]  # 第一個向量
y = [4, 6]  # 第二個向量# 計算閔可夫斯基距離
def minkowski_distance(x, y, p):"""計算兩個向量之間的閔可夫斯基距離參數:x -- 第一個輸入向量y -- 第二個輸入向量p -- 距離參數返回:兩個向量之間的閔可夫斯基距離當p=1時返回曼哈頓距離當p=2時返回歐式距離當p趨近無窮時返回切比雪夫距離"""x = np.array(x)  # 轉換為numpy數組y = np.array(y)  # 轉換為numpy數組if p == 1 or p == 2:  # 當p為1或2時使用標準閔可夫斯基公式test = np.power(np.sum(np.power(np.abs(x - y), p)), 1 / p)return testelse:  # 其他情況返回切比雪夫距離(即最大絕對差)return np.max(np.abs(x - y))md = minkowski_distance(x, y, 1)  # 計算距離
print("曼哈頓距離:", md)  # 輸出結果
md = minkowski_distance(x, y, 2)  # 計算距離
print("歐氏距離：", md)  # 輸出結果
md = minkowski_distance(x, y, 3)  # 計算距離
print("切比雪夫距離：", md)  # 輸出結果

D:\python_huanjing\.venv1\Scripts\python.exe C:\Users\98317\PycharmProjects\study_python\機器學習\day4_15.py 
曼哈頓距離: 7.0
歐氏距離： 5.0
切比雪夫距離： 4進程已結束，退出代碼為 0

小結

1 閔氏距離，包括曼哈頓距離、歐氏距離和切比雪夫距離都存在明顯的缺點:

e.g. 二維樣本(身高[單位:cm],體重[單位:kg]),現有三個樣本：a(180,50)，b(190,50)，c(180,60)。

a與b的閔氏距離（無論是曼哈頓距離、歐氏距離或切比雪夫距離）等于a與c的閔氏距離。但實際上身高的10cm并不能和體重的10kg劃等號。

2 閔氏距離的缺點：

?(1)將各個分量的量綱(scale)，也就是“單位”相同的看待了;

?(2)未考慮各個分量的分布（期望，方差等）可能是不同的。
?(3) 使用參數p實際上可能會很麻煩

四、余弦距離(Cosine Distance)

定義：余弦相似度是兩個向量之間的夾角余弦值，表示兩個向量的方向差異，而不是長度差異。

二維空間中向量A(x1,y1)與向量B(x2,y2)的夾角余弦公式：

兩個n維樣本點a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夾角余弦為：

即：

缺點：余弦相似度無法捕捉向量的幅度信息，只考慮方向。

import mathx = [1, 1]
y = [2, -2]#計算余弦距離
def cosine_distance(x, y):"""計算兩個向量之間的余弦距離參數:x (list): 第一個向量y (list): 第二個向量返回:float: 余弦相似度值，范圍[0,1]"""#分子為0fz = 0#分母為0fm_x = 0fm_y = 0for a, b in zip(x, y):#分子：向量點積fz = fz + a * b#分母：向量模的乘積fm_x = fm_x + a ** 2fm_y = fm_y + b ** 2fm = math.sqrt(fm_x) * math.sqrt(fm_y)if fz > 0:return fz / fmelse:return 0md = cosine_distance(x, y)
print(md)

D:\python_huanjing\.venv1\Scripts\python.exe C:\Users\98317\PycharmProjects\study_python\機器學習\day4_15.py 
0進程已結束，退出代碼為 0

五、杰卡德距離(Jaccard Distance)

杰卡德相似系數(Jaccard similarity coefficient)：兩個集合A和B的交集元素在A，B的并集中所占的比例，稱為兩個集合的杰卡德相似系數，用符號J(A,B)表示：

缺點：它受到數據大小的很大影響。大型數據集可能會對相似系數產生很大影響，因為數據量很大的話可能顯著增加并集，同時保持交集不變。

杰卡德距離(Jaccard Distance)：與杰卡德相似系數相反，用兩個集合中不同元素占所有元素的比例來衡量兩個集合的區分度：

import math
import numpy as np# 定義兩個集合用于計算Jaccard相似系數
x_set = {1, 2, 3}
y_set = {2, 3, 4}def jaccrd_similarity_coefficient(x_set, y_set):"""計算兩個集合之間的Jaccard相似系數參數:x_set: 第一個輸入集合y_set: 第二個輸入集合返回:float: Jaccard相似系數值，范圍[0,1]當兩個集合的并集為空時返回0"""# 計算交集大小intersection = len(set(x_set) & set(y_set))# 計算并集大小union = len(set(x_set) | set(y_set))if (union > 0):return intersection / unionreturn 0# 計算并打印Jaccard距離(1-相似系數)
jsc = jaccrd_similarity_coefficient(x_set, y_set)
print(f"jsc距離 :{1 - jsc}")

D:\python_huanjing\.venv1\Scripts\python.exe C:\Users\98317\PycharmProjects\study_python\機器學習\day4_15.py 
jsc距離 :0.5進程已結束，退出代碼為 0

六、交叉驗證方法

交叉驗證是在機器學習建立模型和驗證模型參數時常用的辦法，一般被用于評估一個機器學習模型的表現。更多的情況下，我們也用交叉驗證來進行模型選擇(model selection)。

6.1 HoldOut Cross-validation（Train-Test Split）（保留交叉驗證）

在這種交叉驗證技術中，整個數據集被隨機地劃分為訓練集和驗證集。根據經驗法則，整個數據集的近70%被用作訓練集，其余30%被用作驗證集。也就是我們最常使用的，直接劃分數據集的方法。

6.2 K-折交叉驗證（K-fold Cross Validation，記為K-CV）

模型的最終準確度是通過取k個模型驗證數據的平均準確度來計算的。

#kfold交叉驗證
from sklearn.model_selection import KFold
from sklearn.datasets import load_iris#獲得數據
iris = load_iris()  # 加載iris數據集
# iris數據集，X是特征，Y是標簽
X = iris.data  # 特征數據
Y = iris.target  # 目標標簽
#申請一個對象
kf = KFold()  # 創建KFold對象，默認n_splits=5
for i, (train_index, test_index) in enumerate(kf.split(X)):"""執行K折交叉驗證參數:train_index: 訓練集索引數組test_index: 測試集索引數組輸出:打印每折的訓練集和測試集索引"""print(f"Fold{i + 1}")print(f"  Train: index={train_index}")print(f"  Test:  index={test_index}")

七、前向傳播與損失函數反向傳播的學習率與梯度下降

7.1 求導法則

從以下幾個方面對求導法則進行介紹
1.導數的含義
2.常見的導數
3.不可微函數
4.導數的求導法則
5.偏導數
6.梯度
上面這6個方面的內容，讓大家，掌握并理解求導法則，為后續學習機器學習算法的學習奠定基礎。

7.1.1 導數含義

1.導數（Derivative），也叫導函數值。又名微商，是微積分中的重要基礎概念。當函數y=f（x）的自變量x在一點x0上產生一個增量Δx時，函數輸出值的增量Δy與自變量增量Δx的比值在Δx趨于0時的極限a如果存在，a即為在x0處的導數，記作f'(x0)或df(x0）/dx。

2.為什么要學習微積分或者說求導？

在機器學習(或者深度學習中)，絕大部分任務是構建一個損失函數，然后去最小化它，這個優化過程使用的就是微分，也可以說是求導。

7.1.1.1舉例子理解

舉2個非常簡單、非常形象的例子，來理解一下導數為啥這樣定義?

例1：速度(小車在馬路上勻速的前進)：

一段路程共900米，小車均速走了30s。在17.5s時，小車運動多快？

問題1：在17.5s時，小車運動多快？

小學數學就學過速度，也叫速率，表示運動物體運動的距離隨時間的變化率，s=vt的公式大家都會。

高中物理開始嚴謹一些，會更專業地區分“位移”“速度”（向量）和“距離”“速率”（無方向的標量），公式還是s=vt，但是表示的內容不同了。

這里我們就用簡單的小學數學知識：

一輛小車在水平直線上勻速運動，它運動的速率v是不變的，因此運動的距離與時間成正比，也就是s=vt，這里，速率v就是距離s隨t的變化率，距離s可以看作是時間t的函數。

為了方便起見，我們用x代表時間（代替t），f(x)代表距離，就是函數：f(x)=vx。

這里v就是函數的變化率，該函數的導數就是：f'(x)=v（后面會學如何求導）。

表示在任何時刻，小車距離變化的趨勢都是v，時間每增加一個小小的x，距離就增加vx。

例2：速度(小車在馬路上非勻速的前進)：

一段路程共900米，小車不均速走了30s。在17.5s時，小車運動多快？在0~30s之間，小車的平均運動多快？

通過在不同時間內對小車進行測距離得到下圖

問題1：求在17.5s時，小車運動多快？
補充信息1：

在15s~20s之間，小車的平均運動速度多快？
補充信息2 給15s到20s之間的時間和距離關系表如下所示

通過上面的例子是不是間隔越小計算的速度越準確，下面用更通俗的講解一下。

是不是用下面的公式就可以求17.5s的速度了？

兩種不同的表示方法：

關于導數嚴謹的定義否存在的判別、計算和使用會在大學重頭開始詳細學習，高中只要簡單地知道導數表示變化率、會求導數、會簡單地用導數分析函數的性質即可。
函數f(x)的導數通常用f'(x)來表示，在f的右上角加上小撇。
當導數為正時，函數的變化率是正的，也就是遞增的；
當導數為負時，函數的變化率是負的，也就是遞減的；
當導數為0時，函數的變化率是0，也就是不增也不減，不變。

7.2 什么是導數

導數是函數，完整地叫應該是“導函數”，通常習慣叫“導數”，它是依附于原函數存在的函數。

導數表示函數的變化趨勢：
●既可以表示函數整體的變化趨勢；
●也可以表示部分的變化趨勢
●還可以表示某個點的變化趨勢。
導數也可以粗糙地理解為“函數在某處的切線的斜率”。

7.3 常見的導數

常數的表達式為：

7.3.1線性函數的導數：

線性函數的表達式為：

導數求解方法：

推導出：

2.3二次方程函數的導數：

y=x^2

其導數求解方法：

推導出：

7.3.2 其它常見的導數：

7.2 不可微函數

如果一個點存在導數，那么該點的函數會在該點微分。也就是說，如果要使函數在整個區間內保持微分則該區間中的每個點，都必須存在導數。

2.實際上，并不是所有的函數在每個點上都可以找到導數，這些函數稱為：不可微函數。
eg: f(x)=|x|

證明過程：
函數f(x)=∣x∣在x=0處不可導的原因是因為該點的左導數和右導數不相等。具體來說：
●當x<0時，f(x)=?x，因此左導數為?1（即函數值隨x的減小而增大）。
●當x>0時，f(x)=x，因此右導數為1（即函數值隨x的增大而增大）。由于左導數和右導數在這點上不相等（左導數為-1，右導數為1），根據可導性的定義，函數在x=0處不可導。這是因為可導的要求是函數在該點處連續，且左右導數相等，而絕對值函數在x=0處雖然連續，但左右導數的不一致性導致了不可導的情況。

7.4 導數的求導法則

7.4.1 導數求導法則的定義：

導數是函數值相對于自變量的瞬時變化率，求導數是一個取極限的過程。對于一個連續且可導的函數，其導數的定義如下

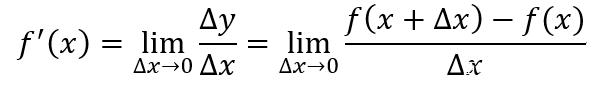
函數可導的前提是函數必須連續，對于連續函數，有下列等式成立

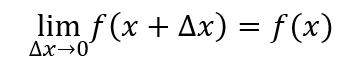
上式是函數在x處連續的定義。結合連續函數的定義和極限的運算性質，我們接下來推導導數運算法則。

7.4.2 兩個函數相加的導數

設F(x)為兩個可導函數的和

那么根據導數定義，F(x)的導數為

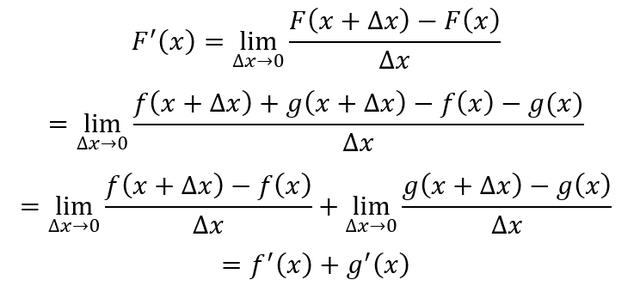
即兩個可導函數的和的導數等于導數的和，導數運算減法同理。

7.4.3 兩個函數乘積的導數

假設G(x)為兩個可導函數的積

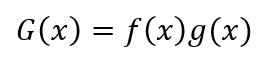
根據導數定義，G(x)的導數為

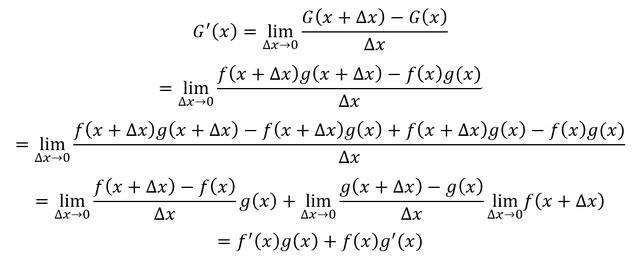
兩個可導函數的乘積的導數的結果為

7.4.4 兩個函數的比值的導數

設H(x)為兩個可導函數的比值

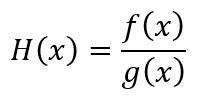
根據導數定義，那么H(x)的導數為

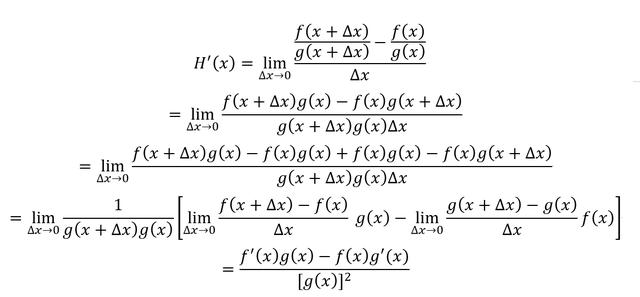
兩個可導函數的比值的導數結果為

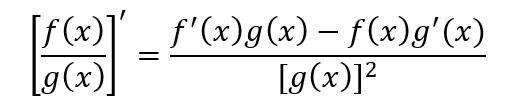
掌握推導過程可以幫助理解導數的定義和運算。

7.5 復合求導運算：

y=(sinx)^2

求導一下 y=2sinxcosx=sin2x

7.6 鏈式求導法則：

1）鏈式求導法則，也稱為鏈式法則，是微積分中的一個基本法則，用于求解復合函數的導數。其基本公式為：如果y 是u 的函數，u 是x 的函數，即y=f(u) 且u=g(x)，則 y 對 x 的導數可以表示為：

這個公式表明，復合函數的導數等于內層函數對中間變量的導數乘以中間變量對自變量的導數。
2）鏈式求導法則的應用非常廣泛，不僅限于一元函數的情況，還可以推廣到多元函數的情況。在應用鏈式法則時，需要明確函數的復合情況及變量的關系，通過畫出鏈式圖，然后運用公式進行求導。

7.7 偏導數

7.7.1 偏導數定義

偏導數是一個多變量函數中關于其中一個變量的導數，同時保持其他變量恒定。

偏導例子
eg1:

對x求偏導數，y當作常數，結果為：

對y求偏導數，x當作常數，結果為：

eg2:

對x求偏導數，y當作常數，結果為：

對y求偏導數，x當作常數，結果為

7.8 梯度

梯度通俗講就是偏導的集合

梯度的例子

八、前向傳播與損失函數

以下2個方面對前向傳播與損失函數進行介紹
1.前向傳播與損失函數理論講解
2.編程實例與步驟
上面這2方面的內容，讓大家，掌握并理解前向傳播與損失函數。

8.1 前向傳播與損失函數理論講解

?8.1.1 前向傳播的定義

前向傳播是指在機器學習算法中，從輸入到輸出的信息傳遞過程，具體來說，就是在數據輸入后，經過一系列的運算后得到結果的過程。
輸入x 經過一系列計算f(x) 得到y的過程
比如y=2x+3,這個公式，前向傳播就是通過給定x,根據公式2x+3得到輸出結果y的值的過程就是前向傳播。

8.1.2 前向傳播的過程

step1：輸入層，輸入數據首先需要進入輸入層，每一個神經元都會接收一個信號(輸入值(矩陣))

step2:輸入層到隱藏層，輸入層的輸出作為下一層的輸入(通常是隱藏層)，通過與權重相乘加上偏置項后進行非線性變換?，使用激活函數對隱藏層的輸出進行非線性變換，以引入非線性特性，增強模型的表達能力。

step3:隱藏層到輸出層?：將隱藏層的輸出乘以隱藏層到輸出層的權重矩陣，再加上偏置，計算輸出層的輸出。

8.1.3 前向傳播的作用

對數據的輸入逐步處理，提取對應的特征，并進行預測.

8.1.4 損失函數的概念：

損失函數（Loss Function）是用來衡量模型預測結果與實際結果之間的差異的一種函數。在機器學習中，損失函數通常被用來優化模型，通過最小化損失函數來提高模型的預測準確率。

8.2 基礎原理講解

8.2.1 案例導入

例子：

池塘里有7只蝌蚪，它們的體積（縱坐標）和時間（橫坐標）有關，蝌蚪的體積隨時間的變化。

自變量是時間x（以天為單位），因變量是蝌蚪的體積y（以毫升為單位）。

那么是否可以擬合一條線，來預測在未來的某個時間點，蝌蚪的體積可能會是多少。

8.2.2 前向計算

前向傳播是指在一個機器學習算法中，從輸入到輸出的信息傳遞過程，具體來說，就是在數據輸入后，經過一系列的運算后得到結果(模型預測結果)的過程。

w表示權重 b表示偏置

在本實驗中，為了使用直線來擬合上面7個散點，可以用直線的斜截式方程來進行擬合，給出直線公式：

在前向計算中，為了簡化運算，我們固定b的值為0，而w的值可以任意修改（范圍0-2）。

w=0 w=0.8

也就是說，我們是用一條過原點的直線來擬合這些散點，在該組件中修改w的值可以實時看到直線與散點的位置關系。

8.2.3 單點誤差

由下圖可知，當w等于2的時候“擬合”這些散點和實際的坐標點y軸的差距，由圖上的綠色虛線表示。綠色虛線表示每一個真實的數據點和預測的數據點的差距，也就是數據點損失。

8.2.4 損失函數：均方差

總結

????????本文系統介紹了機器學習中常用的距離度量方法（曼哈頓距離、切比雪夫距離、閔可夫斯基距離、余弦距離、杰卡德距離）及其數學定義、Python實現與優缺點，并探討了交叉驗證方法（HoldOut與K折）的應用場景。此外，深入解析了前向傳播與損失函數的核心原理，包括導數、偏導數、梯度等數學基礎，以及鏈式求導法則在反向傳播中的作用，最后通過蝌蚪體積預測案例演示了前向計算、單點誤差和均方差損失函數的實際應用，為機器學習模型優化提供了理論支撐與實踐指導。