目錄
前言
學習目標
堆排序
TopK問題:
解法一:建立N個數的堆
解法二:建立K個數的堆(最優解)
完整代碼
結束語
前言
上節內容我們詳細講解了堆[數據結構——lesson10.堆及堆的調整算法],接下來我們來講解堆的一個經典應用——TopK問題。
學習目標
- 堆排序
- 掌握堆的應用理解TopK問題
兩種調整算法的復雜度精準剖析🌟🌟🌟
開頭講了兩種堆的調整算法,分別是【向上調整】和【向下調整】,在接口算法實現Push和Pop的時候又用到了它們,以及在建堆這一塊我也對它們分別做了一個分析,所以我們本文的核心就是圍繞這兩個調整算法來的,但是它們兩個到底誰更加優一些呢?
這里就不做過多解釋,直接看圖即可
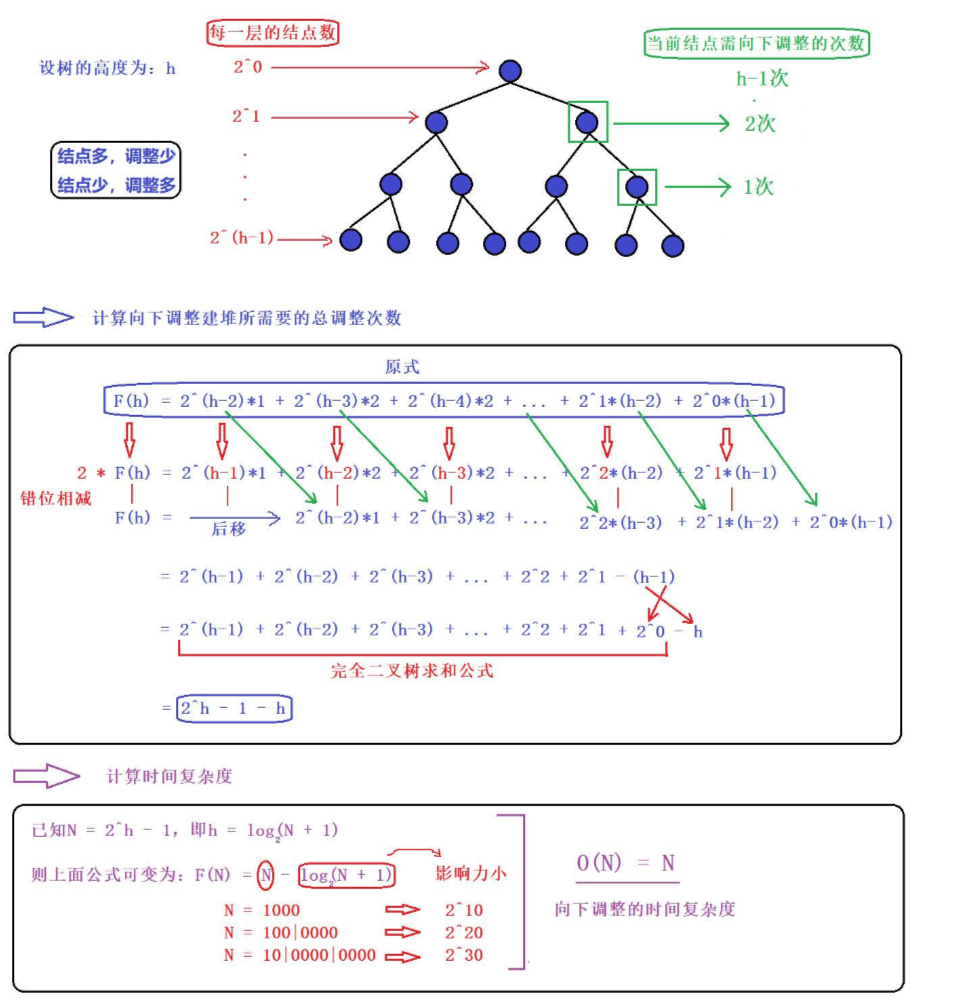
1、向下調整算法【重點掌握】
?
2、向上調整算法
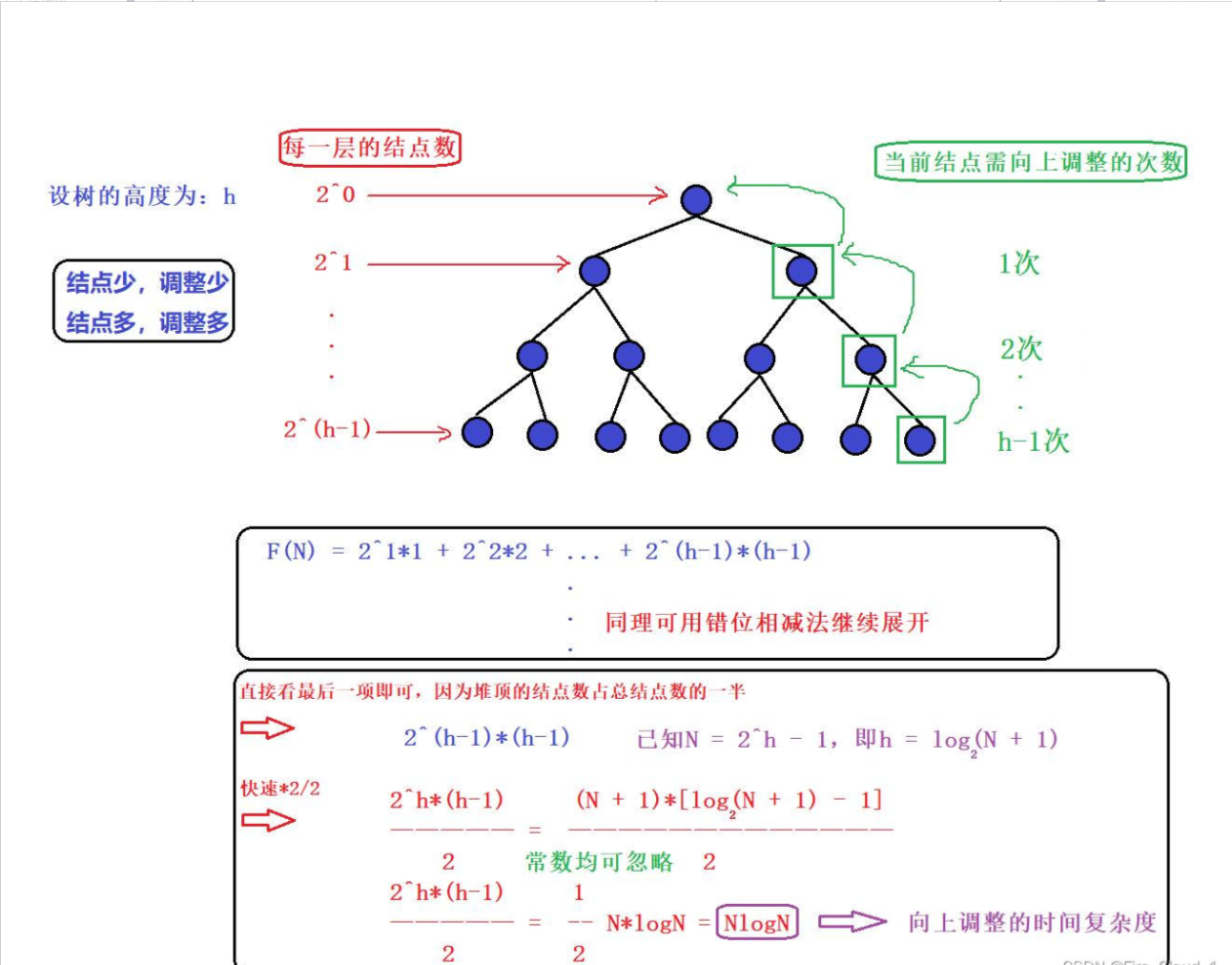
好,我們來總結一下,【向上調整算法】,它的時間復雜度為O(NlogN);【向下調整算法】,它的時間復雜度為O(N)
很明顯,【向下調整算法】來得更優一些,因為向下調整隨著堆的層數增加結點數也會變多,可是結點越多調整得就越少,因為在一些大型數據處理場合我們會使用向下調整
當然在下面要講的堆排序中我們建堆也是利用的向下調整算法,所以大家重點掌握一個就行
?
堆排序
講了那么久的堆,學習了兩種調整算法以及它們的時間復雜度分析,接下去我們來說說一種基于堆的排序算法——【堆排序】
堆排序即利用堆的思想來進行排序,總共分為兩個步驟:1. 建堆
- 升序:建大堆
- 降序:建小堆
這里我們以升序為例(升序建大堆 or 小堆?)
- 在上面解說的時候,我建立的默認都是大堆,但是在這里我們要考慮排序問題了,現在面臨的是【升序】,對于升序就是數組前面的元素小,后面的元素大,這個堆也是基于數組建立的,那就是要堆頂小,堆頂大,很明顯就是建【小堆】
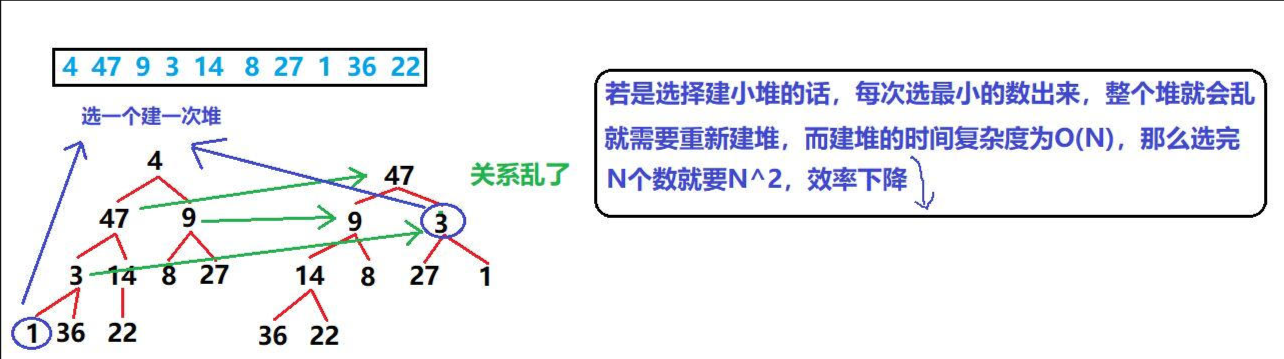
- 一波分析猛如虎🐅,我們通過畫圖來分析是否可以建【小堆】
- 可以看到,對于建小堆來說,原本的左孩子結點就會變成新的根結點,而右孩子結點就會變成新的左孩子結點,整個堆會亂,而且效率并不是很高,因此我們應該反一下,去建大堆
//建立大根堆(倒數第一個非葉子結點) for (int i = ((n - 1) - 1) / 2 ; i >= 0; --i) {Adjust_Down(a, n, i); }所以應建大堆。
?堆排序的基本思路是每次將堆頂元素取出放到有序區間。大堆(大頂堆)中每個節點的值都大于或等于其子節點的值,堆頂元素為最大值。升序排序時建大堆,可將堆頂的最大值與無序區間最后一個數交換,使有序區間增加一個最大值。然后對剩余元素重新調整堆結構,重復此過程,就能逐漸將序列變為升序。
?若升序建小堆,雖然堆頂是最小值,但確定次小值時會很麻煩,因為次小值可能是堆頂的左孩子或右孩子,甚至需要重新建堆,導致排序效率降低。
如何進一步實現排序?
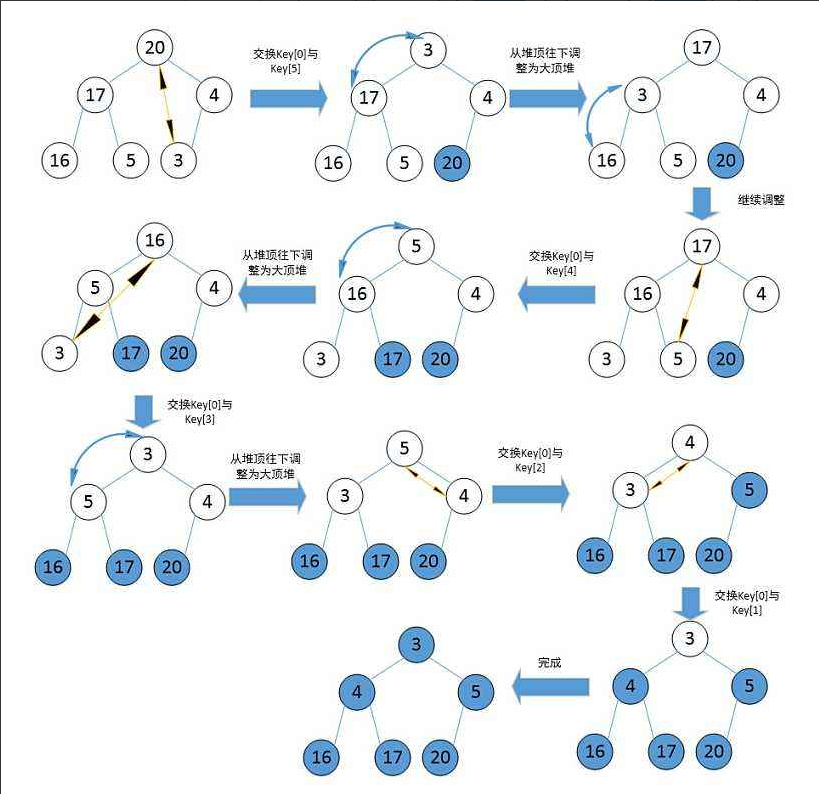
- 有了一個大堆之后,如何去進一步實現升序呢,這里就要使用到在Pop堆頂數據的思路了,也就是現將堆頂數據與堆底末梢數據做一個交換,然后對這個堆頂數據進行一個向下調整,將大的數往上調。具體過程如下
2. 利用堆刪除思想來進行排序建堆和堆刪除中都用到了向下調整,因此掌握了向下調整,就可以完成堆排序。
- 對照代碼,好好分析一下堆排的全過程吧
/*堆排序*/ void HeapSort(int* a, int n) {//建立大根堆(倒數第一個非葉子結點)for (int i = ((n - 1) - 1) / 2 ; i >= 0; --i){Adjust_Down(a, n, i);}int end = n - 1;while (end > 0){swap(&a[0], &a[end]); //首先交換堆頂結點和堆底末梢結點Adjust_Down(a, end, 0); //一一向前調整end--;} }
- 看一下時間復雜度,建堆這一塊是O(N),調整這一塊的話就是每次夠把當前堆中最的數放到堆底來,然后每一個次大的數都需要向下調整O(log2N),數組中有N個數需要調整做排序,因而就是O(Nlog2N)。
- 當然你可以這么去看:第一次放最大的數,第二次是次大的數,這其實和我們上面講過的向上調整差不多了,【結點越少,調整越少;結點越多,調整越多】,因此它也可以使用之前我們分析過的使用的【錯位相減法】去進行求解,算出來也是一個O(Nlog2N)。
- 最后將兩段代碼整合一下,就是O(N + Nlog2N),取影響結果大的那一個就是O(Nlog2N),這也就是堆排序最終的時間復雜度
TopK問題:
Top-K 問題是一類常見的算法和數據處理問題,指從包含 N 個元素的大量數據集合中找到前 K 個最大或最小的元素,通常 N 遠大于 K。
Top-k問題在生活中是非常的常見,比如游戲中某個大區某個英雄熟練度最高的前10個玩家的排名,我們就要根據每個玩家對該英雄的熟練度進行排序,可能有200萬個玩家,但我只想選出前10個,要對所有人去排個序嗎?顯然沒這個必要。
再比如:專業前10名、世界500強、富豪榜、游戲中前100的活躍玩家等。
?
- 問題特點:數據量 N 極大時,若直接對所有數據排序(如快排,時間復雜度為 O (n log n)),不僅耗時久,還可能需將所有數據加載到內存,空間成本極高。而 K 通常很小,只需關注 “最大或最小的前 K 個”,無需對所有數據排序,因此需要更高效的算法來解決。
解法一:建立N個數的堆
建一個 N 個數的堆(C++中可用優先級隊列priority_queue),不斷的選數,選出前 k 個。
時間復雜度:建N個數的堆為O(N),獲取堆頂元素 (也即是最值) 并刪除掉堆頂元素為O(log2N),上述操作重復 k 次,所以時間復雜度為O(N+k*log2N)。
【思考】
但是這樣也會存在上述所講的可能需將所有數據加載到內存,空間成本極高的問題,能否再優化一下呢?
解法二:建立K個數的堆(最優解)
解決思路(堆排序)
- 若要找前 K 個最大的元素,則建立小頂堆;
- 若要找前 K 個最小的元素,則建立大頂堆。
- 首先用數據集合中前 K 個元素來建堆,然后將剩余的 N-K 個元素依次與堆頂元素比較;
- 若大于(針對小頂堆)或小于(針對大頂堆)堆頂元素,則替換堆頂元素并重新調整堆;
- 遍歷完剩余元素后,堆中的 K 個元素就是所求的前 K 個最大或最小的元素。
時間復雜度:
? 建 k 個元素的堆為O(K);
? 遍歷剩余的 N-K 個元素的時間代價為O(N-K),假設運氣很差,每次遍歷都入堆調整;
? 入堆調整:刪除堆頂元素和插入元素都為O(log2K);
? 所以時間復雜度為O(k + (N-K)log2K)。當 N 遠大于 K 時,為O(N*log2K),這種解法更優。
?假如要找出最大的前 10 個數:
? 建立 10 個元素的小堆,數據集合中前 10 個元素依次放入小堆,此時的堆頂元素是堆中最小的元素,也是堆里面第 10 個最小的元素,
? ?然后把數據集合中剩下的元素與堆頂比較,若大于堆頂則去掉堆頂,再將其插入,
? ?這樣一來,堆里面存放的就是數據集合中的前 10 個最大元素,
此時小堆的堆頂元素也就是堆中的第 10 個最大的元素
?思考:為什么找出最大的前10個數,不能建大堆呢?
- 找出最大的前 10 個數不能建大堆,原因在于大堆的特性會導致只能找到最大的數,而無法找到其余較大的數。
- 大堆的性質是堆頂元素為堆中最大的元素。當使用 10 個元素建大堆時,堆頂就是這 10 個元素中最大的,若數據集合中還有其他更大的數,由于它們都小于當前堆頂元素,根據大堆的插入規則,這些數無法進入堆中。所以最終只能得到最大的那個數,無法找出前 10 個最大的數。
- 相反,若建立小堆,堆頂是堆中最小的元素,當有比堆頂大的元素出現時,就可以替換堆頂元素,并通過調整堆結構使小堆性質得以維持,這樣就能保證較大的數逐漸進入堆中,最終堆中的 10 個元素就是數據集合中前 10 個最大的數。
完整代碼
以從1w個數里找出最大的前10個數為例:
#define _CRT_SECURE_NO_WARNINGS
#include<stdlib.h>
#include<stdio.h>
#include<time.h>// 大堆調整
void max_heapify(int* arr, int i, int size)
{int largest = i;int left = 2 * i + 1;int right = 2 * i + 2;if (left < size && arr[left] > arr[largest])largest = left;if (right < size && arr[right] > arr[largest])largest = right;if (largest != i){int temp = arr[i];arr[i] = arr[largest];arr[largest] = temp;max_heapify(arr, largest, size);}
}// 構建大根堆
void build_max_heap(int* arr, int size)
{for (int i = size / 2 - 1; i >= 0; i--)max_heapify(arr, i, size);
}// 堆排序
void heap_sort(int* arr, int size)
{build_max_heap(arr, size);for (int i = size - 1; i > 0; i--) {int temp = arr[0];arr[0] = arr[i];arr[i] = temp;max_heapify(arr, 0, i);}
}// 獲取前k個最小元素
void get_topk_smallest(int* arr, int n, int k, int* result)
{if (k > n) k = n;int* heap = (int*)malloc(k * sizeof(int));if (heap == NULL) {printf("內存分配失敗\n");return;}// 取前k個元素構建大堆for (int i = 0; i < k; i++)heap[i] = arr[i];build_max_heap(heap, k);// 遍歷剩余元素for (int i = k; i < n; i++){if (arr[i] < heap[0]){heap[0] = arr[i];max_heapify(heap, 0, k);}}// 排序結果并輸出heap_sort(heap, k);for (int i = 0; i < k; i++)result[i] = heap[i];free(heap);
}// 生成隨機數組
void generate_random_array(int* arr, int size, int min, int max)
{srand(time(NULL));for (int i = 0; i < size; i++){arr[i] = min + rand() % (max - min + 1);}
}// 打印數組
void print_array(int* arr, int size)
{for (int i = 0; i < size; i++){printf("%d ", arr[i]);if ((i + 1) % 10 == 0)printf("\n");}printf("\n");
}// 驗證結果正確性(通過全排序對比)
void verify_result(int* arr, int n, int k, int* topk)
{// 創建數組副本并排序int* copy = (int*)malloc(n * sizeof(int));for (int i = 0; i < n; i++)copy[i] = arr[i];heap_sort(copy, n); // 注意:這里堆排序是升序printf("\n驗證結果(前10個最小元素):\n");printf("算法結果:");for (int i = 0; i < k; i++)printf("%d ", topk[i]);printf("\n正確結果:");for (int i = 0; i < k; i++)printf("%d ", copy[i]);printf("\n");// 檢查是否一致int correct = 1;for (int i = 0; i < k; i++){if (topk[i] != copy[i]){correct = 0;break;}}printf("驗證結果:%s\n", correct ? "正確" : "錯誤");free(copy);
}int main()
{const int N = 10000; // 數據總量const int K = 10; // 要找的最小元素個數int* arr = (int*)malloc(N * sizeof(int));int* topk = (int*)malloc(K * sizeof(int));// 生成10000個1到100000之間的隨機數generate_random_array(arr, N, 1, 100000);printf("已生成10000個隨機數\n");// 計算前10個最小元素clock_t start = clock();get_topk_smallest(arr, N, K, topk);clock_t end = clock();// 輸出結果printf("\n最小的前10個數(升序排列):\n");print_array(topk, K);// 輸出耗時double time_spent = (double)(end - start) / CLOCKS_PER_SEC;printf("計算耗時:%.6f秒\n", time_spent);// 驗證結果verify_result(arr, N, K, topk);// 釋放內存free(arr);free(topk);return 0;
}運行結果:
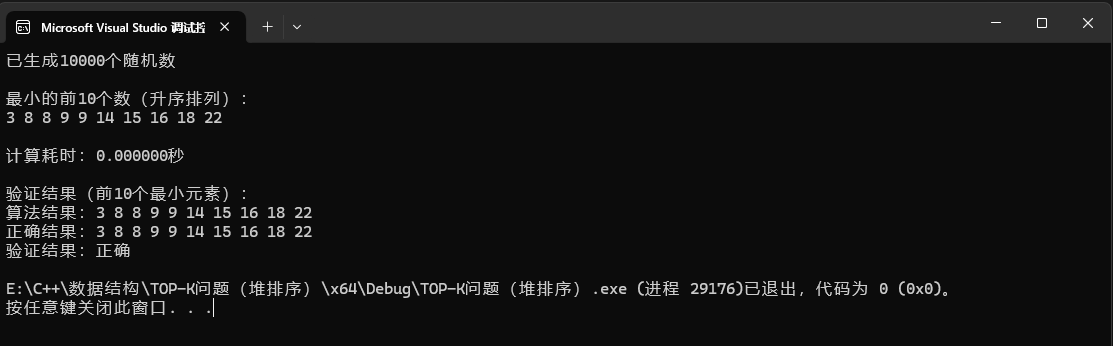
結束語
經過上節堆的學習,這一節我們對于堆的Top K問題的學習與理解相對會輕松很多。
感謝您的三連支持!!!












![基于ssm的小橘子出行客戶體驗評價系統[SSM]-計算機畢業設計源碼+LW文檔](http://pic.xiahunao.cn/基于ssm的小橘子出行客戶體驗評價系統[SSM]-計算機畢業設計源碼+LW文檔)

算法——形象化講解)

:是否有市場空間?)



