定義：回溯法也可以叫做回溯搜索法，它是一種搜索的方式。

回溯是遞歸的副產品，只要有遞歸就會有回溯。

應用場景：回溯法解決的問題都可以抽象為樹形結構

集合的大小就構成了樹的寬度，遞歸的深度就構成了樹的深度。
組合問題：N個數里面按一定規則找出k個數的集合
切割問題：一個字符串按一定規則有幾種切割方式
子集問題：一個N個數的集合里有多少符合條件的子集
排列問題：N個數按一定規則全排列，有幾種排列方式
棋盤問題：N皇后，解數獨等等

代碼模板

void backtracking(參數) {if (終止條件) {存放結果;return;}for (選擇：本層集合中元素（樹中節點孩子的數量就是集合的大小）) {處理節點;backtracking(路徑，選擇列表); // 遞歸回溯，撤銷處理結果}
}

題型

第77題. 組合

給定兩個整數 n 和 k，返回 1 … n 中所有可能的 k 個數的組合。

示例: 輸入: n = 4, k = 2 輸出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]

思路：每次從集合中選取元素，可選擇的范圍隨著選擇的進行而收縮，調整可選擇的范圍。

圖中可以發現n相當于樹的寬度，k相當于樹的深度。
圖中每次搜索到了葉子節點，我們就找到了一個結果。
把達到葉子節點的結果收集起來，就可以求得 n個數中k個數的組合集合。

class Solution {
private:vector<vector<int>> result; // 存放符合條件結果的集合vector<int> path; // 用來存放符合條件結果void backtracking(int n, int k, int startIndex) {if (path.size() == k) {result.push_back(path);return;}for (int i = startIndex; i <= n; i++) {path.push_back(i); // 處理節點backtracking(n, k, i + 1); // 遞歸path.pop_back(); // 回溯，撤銷處理的節點}}
public:vector<vector<int>> combine(int n, int k) {result.clear(); // 可以不寫path.clear();   // 可以不寫backtracking(n, k, 1);return result;}
};

216.組合總和III

找出所有相加之和為 n 的 k 個數的組合。組合中只允許含有 1 - 9 的正整數，并且每種組合中不存在重復的數字。

思路：本題k相當于樹的深度，9（因為整個集合就是9個數）就是樹的寬度。

一維數組path來存放符合條件的結果，二維數組result來存放結果集。

class Solution {
private:vector<vector<int>> result; // 存放結果集vector<int> path; // 符合條件的結果// targetSum：目標和，也就是題目中的n。// k：題目中要求k個數的集合。// sum：已經收集的元素的總和，也就是path里元素的總和。// startIndex：下一層for循環搜索的起始位置。void backtracking(int targetSum, int k, int sum, int startIndex) {if (path.size() == k) {if (sum == targetSum) result.push_back(path);return; // 如果path.size() == k 但sum != targetSum 直接返回}for (int i = startIndex; i <= 9; i++) {sum += i; // 處理path.push_back(i); // 處理backtracking(targetSum, k, sum, i + 1); // 注意i+1調整startIndexsum -= i; // 回溯path.pop_back(); // 回溯}}public:vector<vector<int>> combinationSum3(int k, int n) {result.clear(); // 可以不加path.clear();   // 可以不加backtracking(n, k, 0, 1);return result;}
};

17.電話號碼的字母組合

給定一個僅包含數字 2-9 的字符串，返回所有它能表示的字母組合。

給出數字到字母的映射如下（與電話按鍵相同）。注意 1 不對應任何字母。

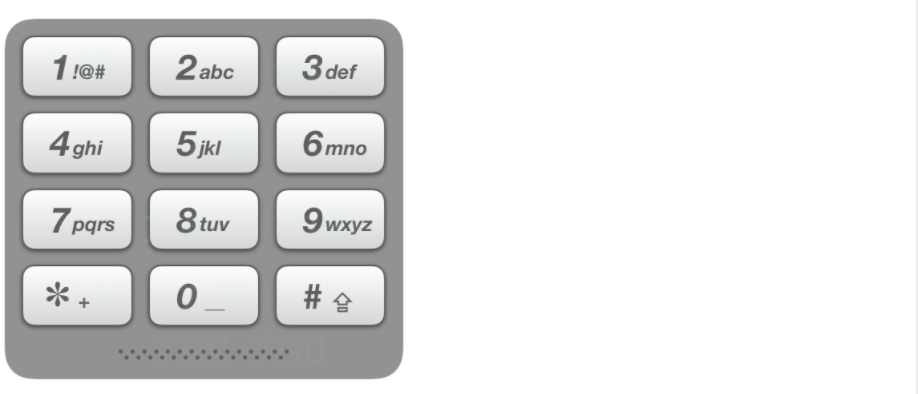
思路：求不同集合之間的組合

class Solution {
private:const string letterMap[10] = {"", // 0"", // 1"abc", // 2"def", // 3"ghi", // 4"jkl", // 5"mno", // 6"pqrs", // 7"tuv", // 8"wxyz", // 9};
public:vector<string> result;string s;void backtracking(const string& digits, int index) {if (index == digits.size()) {result.push_back(s);return;}int digit = digits[index] - '0';        // 將index指向的數字轉為intstring letters = letterMap[digit];      // 取數字對應的字符集for (int i = 0; i < letters.size(); i++) {s.push_back(letters[i]);            // 處理backtracking(digits, index + 1);    // 遞歸，注意index+1，一下層要處理下一個數字了s.pop_back();                       // 回溯}}vector<string> letterCombinations(string digits) {s.clear();result.clear();if (digits.size() == 0) {return result;}backtracking(digits, 0);return result;}
};

39. 組合總和

給定一個無重復元素的數組 candidates 和一個目標數 target ，找出 candidates 中所有可以使數字和為 target 的組合。

candidates 中的數字可以無限制重復被選取。

說明：

所有數字（包括 target）都是正整數。
解集不能包含重復的組合。
示例 1：

輸入：candidates = [2,3,6,7], target = 7,
所求解集為： [ [7], [2,2,3] ]
示例 2：

輸入：candidates = [2,3,5], target = 8,
所求解集為： [ [2,2,2,2], [2,3,3], [3,5] ]

思路：

class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {if (sum > target) {return;}if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size(); i++) {sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i); // 不用i+1了，表示可以重復讀取當前的數sum -= candidates[i];path.pop_back();}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {result.clear();path.clear();backtracking(candidates, target, 0, 0);return result;}
};

40.組合總和II

給定一個數組 candidates 和一個目標數 target ，找出 candidates 中所有可以使數字和為 target 的組合。

candidates 中的每個數字在每個組合中只能使用一次。

說明： 所有數字（包括目標數）都是正整數。解集不能包含重復的組合。

思路：加一個bool型數組used，用來記錄同一樹枝上的元素是否使用過。實現去重

class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {// used[i - 1] == true，說明同一樹枝candidates[i - 1]使用過// used[i - 1] == false，說明同一樹層candidates[i - 1]使用過// 要對同一樹層使用過的元素進行跳過if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {continue;}sum += candidates[i];path.push_back(candidates[i]);used[i] = true;backtracking(candidates, target, sum, i + 1, used); // 和39.組合總和的區別1，這里是i+1，每個數字在每個組合中只能使用一次used[i] = false;sum -= candidates[i];path.pop_back();}}public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<bool> used(candidates.size(), false);path.clear();result.clear();// 首先把給candidates排序，讓其相同的元素都挨在一起。sort(candidates.begin(), candidates.end());backtracking(candidates, target, 0, 0, used);return result;}
};

131.分割回文串

給定一個字符串 s，將 s 分割成一些子串，使每個子串都是回文串。

返回 s 所有可能的分割方案。

示例: 輸入: “aab” 輸出: [ [“aa”,“b”], [“a”,“a”,“b”] ]

思路：

class Solution {
private:vector<vector<string>> result;vector<string> path; // 放已經回文的子串void backtracking (const string& s, int startIndex) {// 如果起始位置已經大于s的大小，說明已經找到了一組分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}for (int i = startIndex; i < s.size(); i++) {if (isPalindrome(s, startIndex, i)) {   // 是回文子串// 獲取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else {                                // 不是回文，跳過continue;}backtracking(s, i + 1); // 尋找i+1為起始位置的子串path.pop_back(); // 回溯過程，彈出本次已經添加的子串}}bool isPalindrome(const string& s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s[i] != s[j]) {return false;}}return true;}
public:vector<vector<string>> partition(string s) {result.clear();path.clear();backtracking(s, 0);return result;}
};

93.復原IP地址

給定一個只包含數字的字符串，復原它并返回所有可能的 IP 地址格式。

有效的 IP 地址 正好由四個整數（每個整數位于 0 到 255 之間組成，且不能含有前導 0），整數之間用 ‘.’ 分隔。

例如：“0.1.2.201” 和 “192.168.1.1” 是 有效的 IP 地址，但是 “0.011.255.245”、“192.168.1.312” 和 “192.168@1.1” 是 無效的 IP 地址。

思路：切割問題就可以使用回溯搜索法把所有可能性搜出來

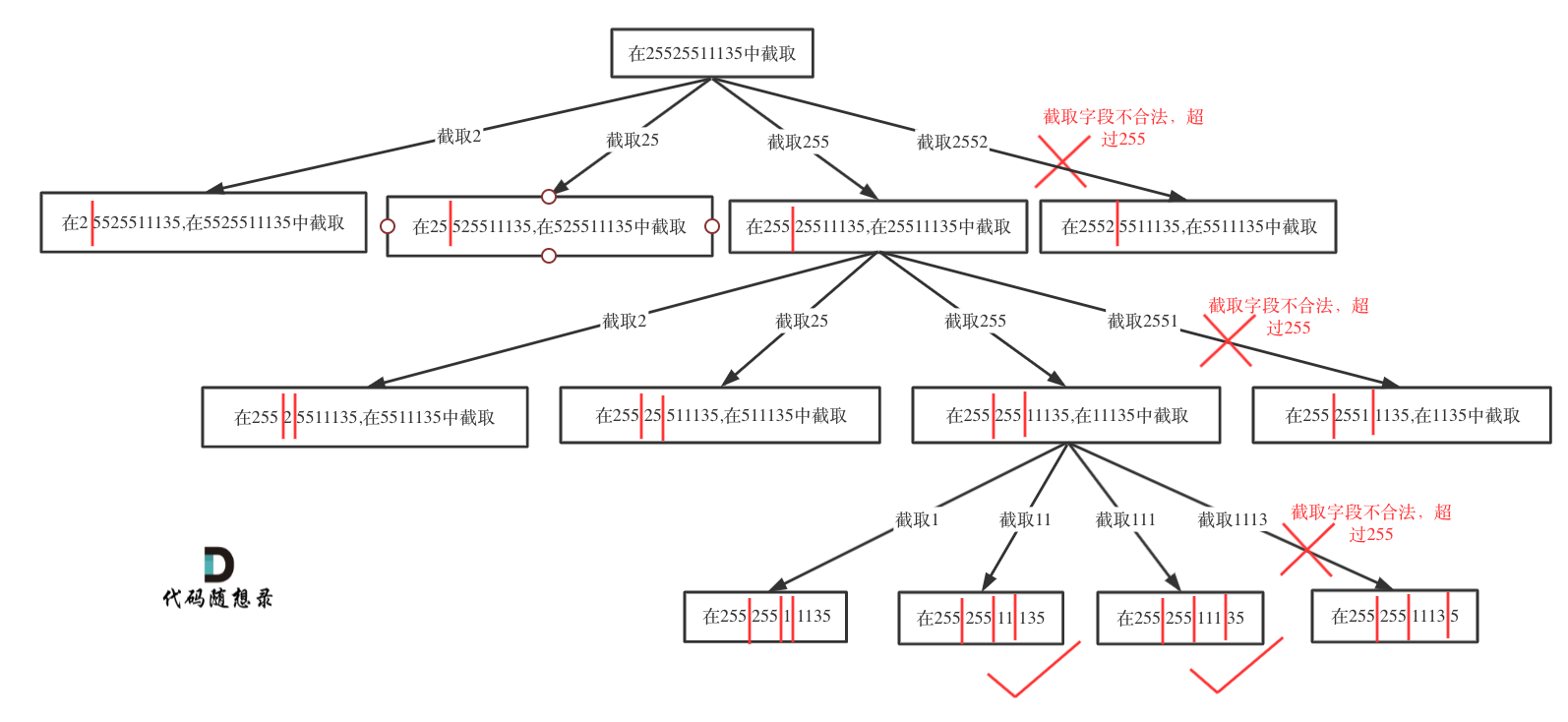
startIndex一定是需要的，因為不能重復分割，記錄下一層遞歸分割的起始位置。

本題我們還需要一個變量pointNum，記錄添加逗點的數量。

class Solution {
private:vector<string> result;// 記錄結果// startIndex: 搜索的起始位置，pointNum:添加逗點的數量void backtracking(string& s, int startIndex, int pointNum) {if (pointNum == 3) { // 逗點數量為3時，分隔結束// 判斷第四段子字符串是否合法，如果合法就放進result中if (isValid(s, startIndex, s.size() - 1)) {result.push_back(s);}return;}for (int i = startIndex; i < s.size(); i++) {if (isValid(s, startIndex, i)) { // 判斷 [startIndex,i] 這個區間的子串是否合法s.insert(s.begin() + i + 1 , '.');  // 在i的后面插入一個逗點pointNum++;backtracking(s, i + 2, pointNum);   // 插入逗點之后下一個子串的起始位置為i+2pointNum--;                         // 回溯s.erase(s.begin() + i + 1);         // 回溯刪掉逗點} else break; // 不合法，直接結束本層循環}}// 判斷字符串s在左閉右閉區間[start, end]所組成的數字是否合法bool isValid(const string& s, int start, int end) {if (start > end) {return false;}if (s[start] == '0' && start != end) { // 0開頭的數字不合法return false;}int num = 0;for (int i = start; i <= end; i++) {if (s[i] > '9' || s[i] < '0') { // 遇到非數字字符不合法return false;}num = num * 10 + (s[i] - '0');if (num > 255) { // 如果大于255了不合法return false;}}return true;}
public:vector<string> restoreIpAddresses(string s) {result.clear();if (s.size() < 4 || s.size() > 12) return result; // 算是剪枝了backtracking(s, 0, 0);return result;}
};

78.子集

給定一組不含重復元素的整數數組 nums，返回該數組所有可能的子集（冪集）。

說明：解集不能包含重復的子集。

思路：子集問題是找樹的所有節點

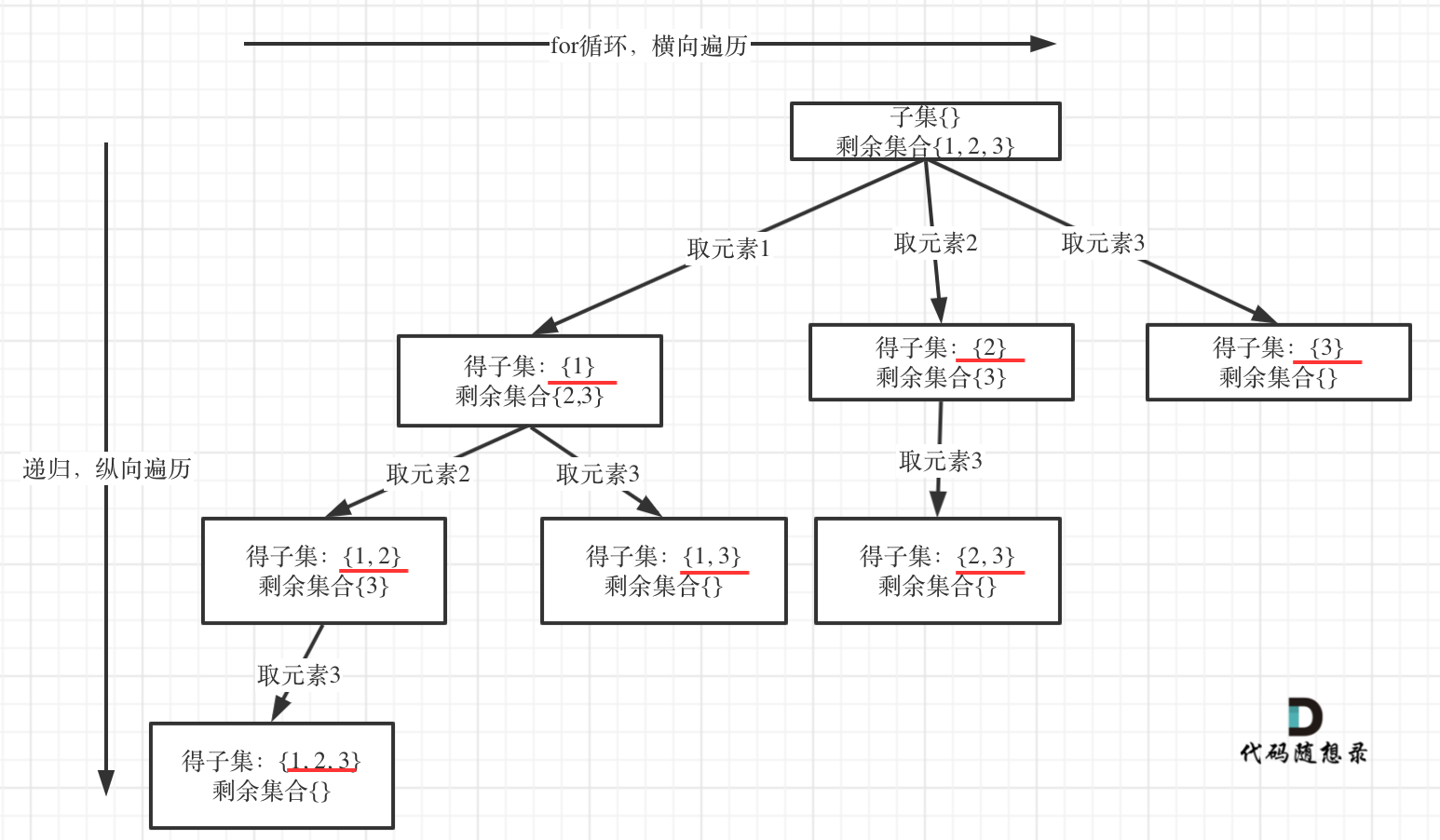
遍歷這個樹的時候，把所有節點都記錄下來，就是要求的子集集合。

class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& nums, int startIndex) {result.push_back(path); // 收集子集，要放在終止添加的上面，否則會漏掉自己if (startIndex >= nums.size()) { // 終止條件可以不加return;}for (int i = startIndex; i < nums.size(); i++) {path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();}}
public:vector<vector<int>> subsets(vector<int>& nums) {result.clear();path.clear();backtracking(nums, 0);return result;}
};