前言:各位老鐵好，在前面博客中，筆者分享了有關二叉樹的博客，在那篇博客中，筆者講到了完全二叉樹的存儲結構中有兩種存儲方式，一種是順序存儲，一種是鏈式存儲，鏈式存儲筆者已經帶各位老鐵實現過了，今天筆者要分享的是，完全二叉樹的順序存儲之堆。

1.堆的定義

那么什么是堆呢？我們肯定知道堆是一個完全二叉樹，但是堆還需要滿足一個條件，那就是每一個父節點的值必須大于等于其所有子節點的值(大根堆)，又或者是每一個父節點的值小于等于其所有子節點的值(小根堆)。
堆的圖示

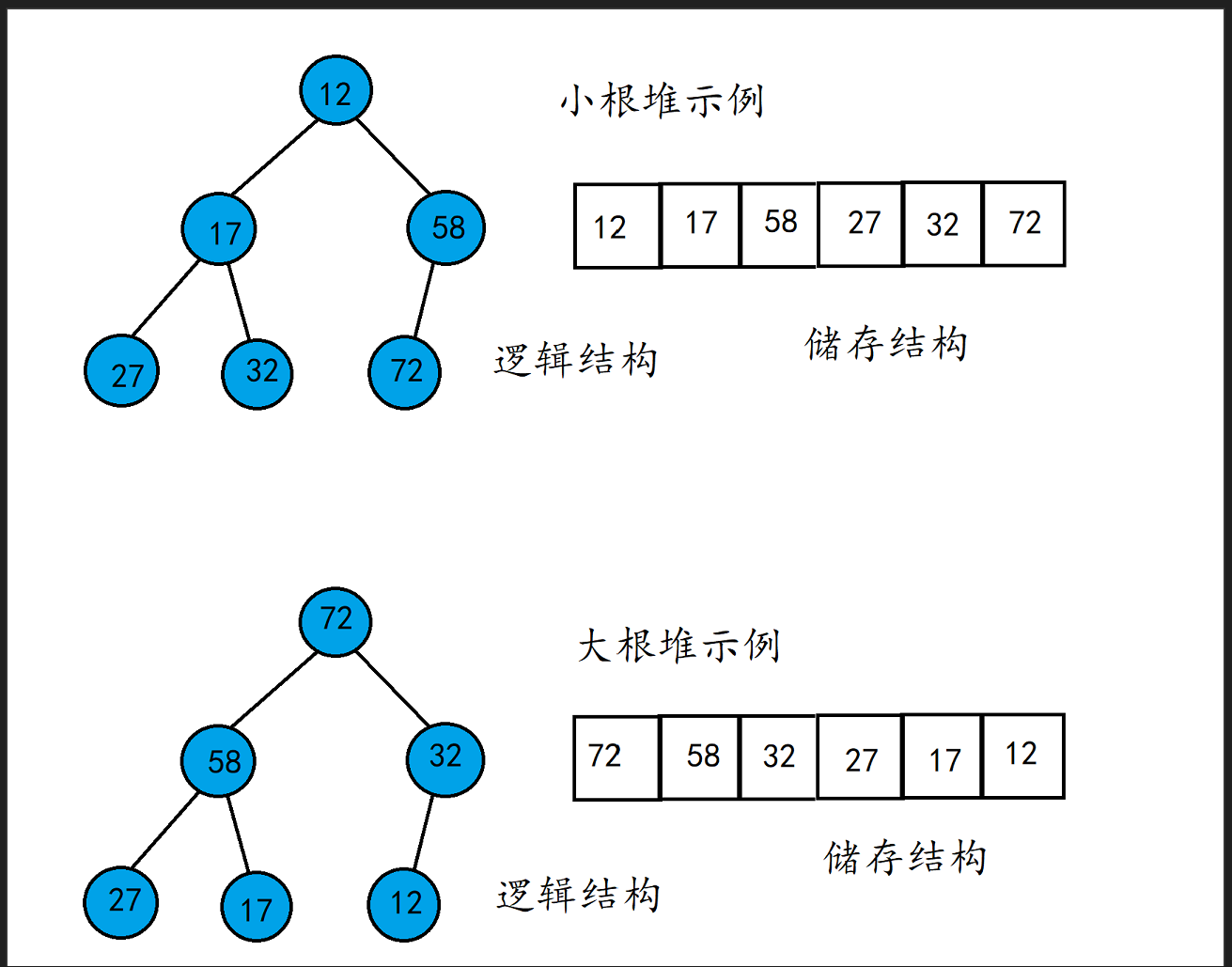
這里提一嘴，堆的實際的存儲結構是數組來存儲，我們一般把堆的邏輯結構看成是特殊的完全二叉樹!!!

那么講完了什么是堆，接下來就到堆實現的重頭戲了。
再將堆結構的實現之前，我們先來鋪墊兩個概念
一個是向下調整算法，一個是向上調整算法

2.向下調整算法:向下調算法是有其中某一個非葉子節點不滿足堆的性質，從而將它進行向下不斷地調整到葉子節點，直到該節點滿足堆地性質，向下調整算法有一個前提，該節點地左右子樹必須滿足堆的性質

可能有老鐵看完筆者文字描述向下調整算法，對向下調整算法還不清楚，沒關系，筆者接下來會舉例加畫圖來給各位老鐵講解。

基于上面的內容，相信各位老鐵一定懂得了向下調整算法了，那么接下來我們就需要來實現出向下調整算法，畢竟光說不練那是假把式嘛!(這里實現的是小根堆的向下調整算法)
我們知道堆的實際存儲結構是數組，那么我們需要給堆傳入一個數組，還需要有一個非葉子節點，因為我們是對非葉子節點進行調整嘛。(現在假設這個節點是根節點)
先定義一個結構體來表示堆(c語言實現，默認堆存儲的整形數據)

#include <stdio.h>
typedef struct Heap
{int* _data;//存放數據int _size;//堆里面元素個數int _capacity;//整個空間大小
}Heap;

那么接下來就是實現向下調整算法了

typedef struct Heap
{int* _data;//存放數據int _size;//堆里面元素個數int _capacity;//整個空間大小
}Heap;//交換兩個節點值
void Swap(int* h1, int* h2)
{int tmp=0;tmp = *h1;*h1 = *h2;*h2 = tmp;
}//n表示堆元素個數
void AdjustDowns(int* a, int n, int root)
{int parent = root;int child = parent * 2 + 1;while (child < n)//只要chlid節點還在堆范圍內,就繼續判斷{//將parent節點和左右子節點進行比較if (child + 1 < n && a[child + 1] < a[child])//右子節點小于左子節點就++chlid{++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//交換兩個節點//更新chlid和parentparent = child;child = parent * 2 + 1;}//比父節點大不需要交換else{break;}}
}

3.向上調整算法:從某個節點開始，不斷與父節點比較和交換，直到該節點滿足堆的性質或者到達根節點為止，也需要滿足除了這個節點的位置，前面的位置已經構成堆了。

筆者認為這個文字描述老鐵們應該能看的懂了，所以筆者就不再畫圖了。
直接來實現向上調整算法了

//向上調整算法
void AdjustUp(int* a, int child)
{//先算出parent節點位置int parent = (child - 1) / 2;//減一是節點下標從0開始while (child > 0)//若該節點不是根節點就繼續調整{if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//更新child和parentchild = parent;parent = (child - 1) / 2;}else{break;}}
}

到這里我們就已經懂得了向上和向下調整算法了，下面我們就開始真正實現堆了。

4.初始化堆

void HeapInit(Heap* php)
{assert(php);//確保傳入的對象不為空php->a = NULL;php->capacity = php->size = 0;
}

5.堆的插入

我們要明白堆的插入分為幾種情況，是不是分為兩種情況，一種是當存放數據的數組滿了，是不是需要擴容才能插入，另一種是數組空間還足夠，可以直接插入。

//堆的末尾插入數據
void HeapPush(Heap* php, int x)
{assert(php);//空間滿了(按兩倍來擴容)if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;int* tmp = (int*)realloc(php->a, sizeof(int) * newcapacity);if (tmp < 0){perror("realloc fail");//perror打印錯誤信息}php->a = tmp;php->capacity = newcapacity;}//插入數據php->a[php->size] = x;php->size++;//進行向上調整AdjustUp(php->a, php->size - 1);
}

6.取堆頂的數據

這個很簡單，直接上代碼了

int HeapTop(Heap* php)
{assert(php);assert(php->size);return php->a[0];
}

7.刪除堆頂數據

如果我們直接刪除堆頂的數據，是不是會破壞完全二叉樹的結構，那么我們就換一種思路，通過將最后一個節點和第一個節點進行交換，然后在刪除最后一個節點，最后再將第一個節點進行向下調整，這樣就保持住了完全二叉樹的結構。

void HeapPop(Heap* php)
{assert(php);assert(php->size > 0);//交換堆頂元素和最后一個元素Swap(&php->a[0], &php->a[php->size - 1]);//刪除最后一個元素php->size--;//最后將第一個節點向下調整AdjustDown(php->a, php->size, 0);
}

8.判斷堆是否為空

這個也很簡單，直接上代碼

bool HeapEmpty(Heap* php)
{assert(php);return php->size == 0;
}

9.釋放堆

void HeapDestroy(Heap* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}

10.有關于堆常考的一個面試題:Topk問題

Topk問題:假設現在有n個數，需要讓你選出最小的前k個數，你該如何選？

法一:使用堆排序，先建立一個大堆(建堆時間復雜度是0(n))，再讓堆頂元素和最后一個元素進行交換，我們知道堆頂元素是當前的最大值，那么每一次交換到當前的最后一個元素，就確保了當前堆頂元素放到該放的位置，進行n-1次進行交換，那么就整個有序了，那么總的時間復雜度是o(n*logn)

法二:我們可以先建立有k個元素的最大堆(堆頂是當前k個元素中的最大值)，那么現在遍歷剩下的n-k個元素，如果比堆頂元素小，那么就替換堆頂，然后再調整，直到替換出最小的前k個元素。

法三:假設現在n=10億，我的內存肯定是存不下了，那么就不能直接使用堆排序了，那么這些值現在在文件中，那么我們該如何找出前k個最小元素

答:也是通過建立k個元素的大堆，再拿10億-k的數據和堆頂數據比較，比堆頂小就替換堆頂并調整，最后一直比較完10億-k個數據，就能找到最小的前k個元素了，那么我的內存僅僅需要維護o(k)