模型創新性

在國賽數學建模中，完備性是論文的基本要求，而創新性則是決定論文能否脫穎而出的關鍵因素。所謂創新，并不僅僅指提出完全新穎的數學理論，而是能夠在已有方法的基礎上，通過新的問題切入點、假設修正、模型優化或求解改進，使模型更契合實際問題、更具解釋力與推廣價值。模型創新性主要體現在以下幾個方面：

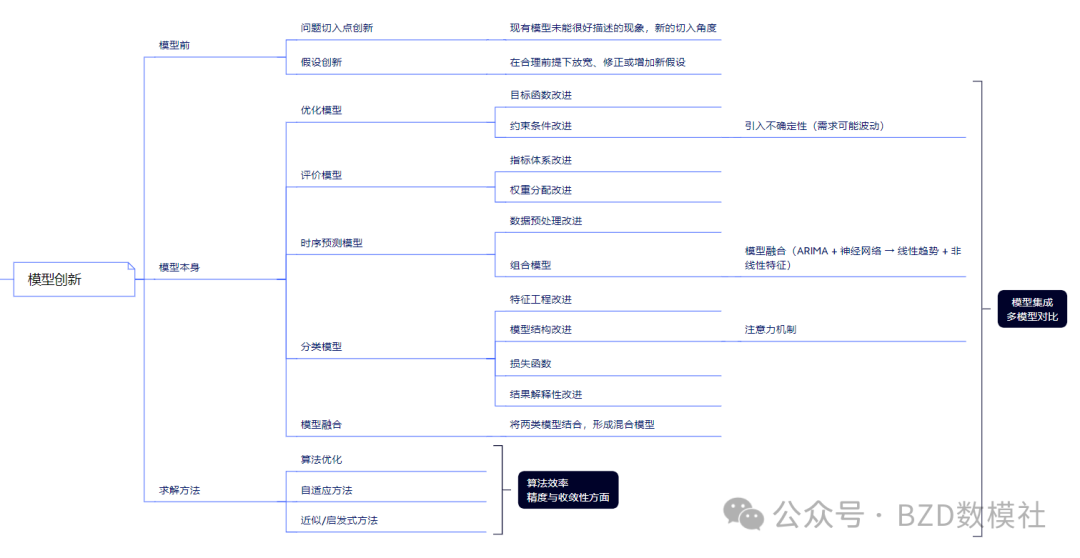
1. 模型前的創新

在建模初始階段，可以通過新的切入點或假設來展現創新思維。

問題切入點創新：針對現有模型無法很好描述的現象，提出新的建模角度。例如，從個體行為出發，而非宏觀總量，建立更具解釋力的微觀模型。

假設創新：在合理前提下，對傳統假設進行放寬、修正或補充。例如，在資源分配問題中引入不完全信息假設，或在預測問題中允許外部環境擾動的存在。

2. 模型本身的創新

模型結構與功能的改進，是創新性的核心體現。

優化模型：在目標函數中引入多目標權衡或動態約束；在約束條件中考慮不確定性因素（如需求波動、價格隨機性）。

評價模型：改進指標體系或權重分配方式，使評價更科學合理；例如采用熵權法、層次分析法等改進傳統平均權重。

時序預測模型：在數據預處理階段引入新方法（如小波分解、滑動窗口），或通過模型融合（如 ARIMA 與神經網絡結合）同時捕捉線性趨勢與非線性特征。

分類模型：在特征工程中構造新特征；在模型結構上引入注意力機制或殘差連接；在損失函數設計中考慮類別不均衡；同時提升模型結果的可解釋性。

模型融合：將不同類型模型結合，形成混合建模框架。例如，將基于機理的物理模型與基于數據的機器學習模型相結合，提升預測精度與適用范圍。

3. 求解方法的創新

在求解過程中對算法進行改進，同樣是論文加分點。

算法優化：改進傳統優化方法的收斂速度與精度。

自適應方法：讓算法參數根據數據特征自動調整，例如自適應學習率方法。

近似/啟發式方法：在復雜模型難以精確求解時，采用啟發式或元啟發式算法（如遺傳算法、模擬退火、粒子群優化）尋找近似最優解，提高計算效率與可行性。