數據集在作業一

異常檢測

異常檢測就是發現與大部分對象不同的對象，其實就是發現離群點。異常檢測有時也稱偏差檢測。異常對象是相對罕見的。用數據集建立概率模型p ( x )，如果新的測試數據在這個模型上小于某個閾值，則說它極大可能為異常點

算法流程：

1.求出均值與方差

2.計算正態分布密度函數

3.找出合適的閾值

代碼實現

讀取數據及可視化

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio# 讀取數據
data=sio.loadmat("ex8data1.mat")
X=data['X']
X_val=data['Xval']
y_val=data['yval']
# print(X.shape)(307, 2)# 可視化
# plt.scatter(X[:,0],X[:,1],marker='o',c='y',edgecolors='g')
# plt.show()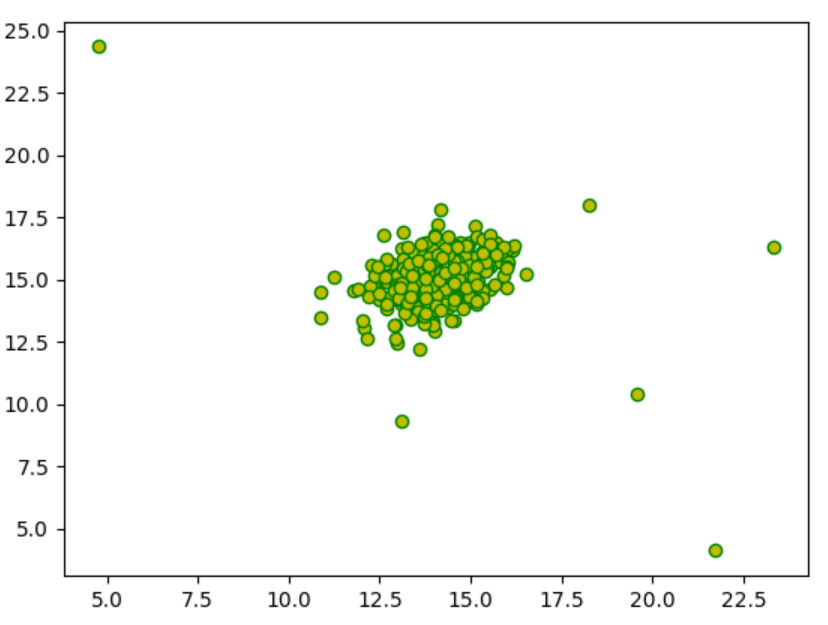

獲取均值和方差

def estimate_gaussian(X,isCovariance):mu=np.mean(X,axis=0)if isCovariance:sigma = np.cov(X.T)else:sigma=np.var(X,axis=0)return mu,sigma

這里的方差有一個不同之處，因為X有多個特征，不能判斷特征之間是否沒有線性關系，若沒有，則按照每列來計算各列的方差，反之，我們就要用協方差。

協方差矩陣

計算概率密度

def gaussian_prob(X,mu,sigma):p=np.zeros((X.shape[0],1))n=len(mu)if np.ndim(sigma) == 1:  # 返回sigma的維度是1sigma = np.diag(sigma)  # 將一維數組轉化為方陣，非對角線元素為0for i in range(X.shape[0]):# 計算公式中的指數部分：-0.5*(x-μ)?Σ?1(x-μ)exponent = -0.5 * (X[i, :] - mu).T @ np.linalg.inv(sigma) @ (X[i, :] - mu)# 計算概率密度值并賦值給p[i]p[i] = (2 * np.pi) ** (-n / 2)  # 公式中的(2π)^(-n/2)p[i] *= np.linalg.det(sigma) ** (-1 / 2)  # 乘以|Σ|^(-1/2)p[i] *= np.exp(exponent)  # 乘以指數部分return pp=gaussian_prob(X,mu,sigma)

繪制梯度密度等高線

def plot_gaussian(X,means,sigma):x=np.arange(0,30,0.5)y=np.arange(0,30,0.5)xx,yy=np.meshgrid(x,y)Z=gaussian_prob(np.c_[xx.ravel(),yy.ravel()],means,sigma)zz=Z.reshape(xx.shape)contour_levels = [10 ** h for h in range(-20, 0, 3)]plt.contour(xx, yy, zz, contour_levels)#生成了 [1e-20, 1e-17, 1e-14, 1e-11, 1e-8, 1e-5, 1e-2] 這 7 個值，# 表示只繪制密度等于這些值的等高線。plt.scatter(X[:, 0], X[:, 1], marker='x', c='b')plt.show()# plot_gaussian(X,mu,sigma)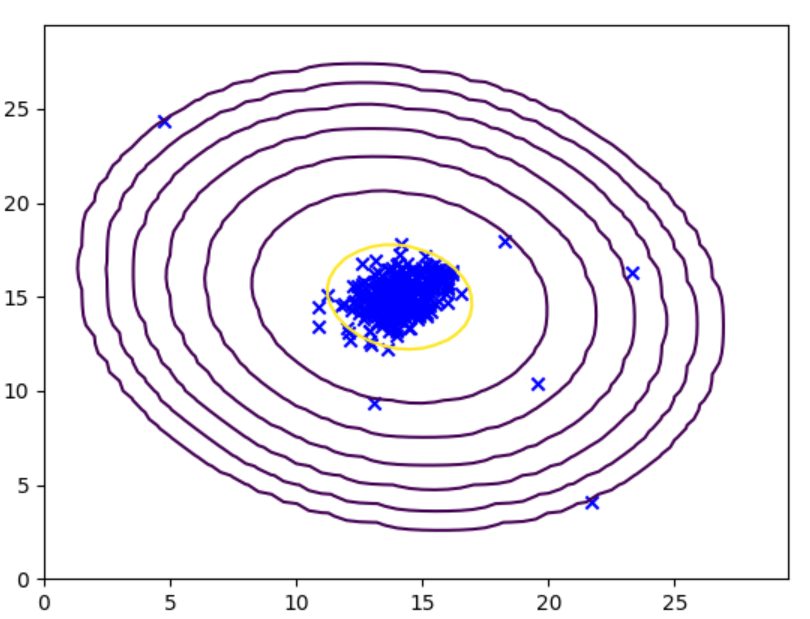

這里是通過取足夠多的點并計算它們的概率密度，從而實現等高線。

找出最佳閾值

#4.閾值epsilonz自取
def selecteps(yval,p):bestEpsilon = 0  # 最佳閾值，初始化為0bestF1 = 0  # 最佳F1分數，初始化為0# 生成1000個候選閾值，均勻分布在p的最小值和最大值之間epsilons = np.linspace(min(p), max(p), 1000)for e in epsilons:# 基于當前閾值e判斷：p < e → 異常（1），否則正常（0）p_ = p < e# 計算混淆矩陣的四個指標tp = np.sum((yval == 1) & (p_ == 1))  # 真正例：實際異常，預測也異常fp = np.sum((yval == 0) & (p_ == 1))  # 假正例：實際正常，預測異常tn = np.sum((yval == 0) & (p_ == 0))  # 真負例：實際正常，預測正常fn = np.sum((yval == 1) & (p_ == 0))  # 假負例：實際異常，預測正常# 計算精確率（Precision）：預測為異常的樣本中，實際異常的比例prec = tp / (tp + fp) if (tp + fp) else 0  # 避免分母為0# 計算召回率（Recall）：實際異常的樣本中，被正確預測的比例rec = tp / (tp + fn) if (tp + fn) else 0  # 避免分母為0# 計算F1分數：精確率和召回率的調和平均，綜合評價模型性能F1 = (2 * prec * rec) / (prec + rec) if (prec + rec) else 0# 更新最佳閾值和F1分數if F1 > bestF1:bestF1 = F1bestEpsilon = ereturn bestF1,bestEpsilonp_val=gaussian_prob(X_val,mu,sigma)
bestF1,bestEpsilon=selecteps(y_val,p_val)

這里利用了混淆矩陣來更新最佳閾值。

圈出異常點

# 圈出異常點
p=gaussian_prob(X,mu,sigma)
anoms = np.array([X[i] for i in range(X.shape[0]) if p[i] < bestEpsilon])
plt.scatter(anoms[:,0], anoms[:,1], s=100, marker='o', facecolors='none', edgecolors='r', linewidths=2)
plot_gaussian(X, mu, sigma)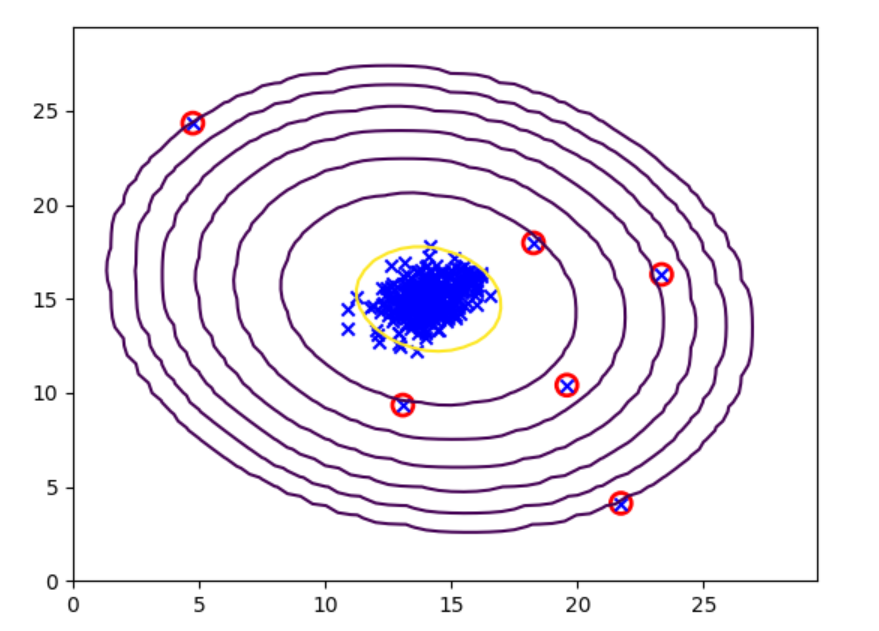

總結

讀取數據——獲取均值與方差——用概率密度函數構建模型——找出最佳閾值——找出異常點。