大家好，今天是2025年8月31日，上一期我給大家分享了 KMP 算法的相關知識，今天我來帶領大家學習4道 KMP 相關的算法題。

在學習算法題之前，還是希望大家能夠要先學會 KMP 算法（可以參考這篇文章：KMP 算法）

當然，如果你是高手的話，也可以自己先嘗試一下解決下面的四道問題，檢驗一下你的 KMP 算法的掌握程度。

那么，廢話不多收，我們開啟今天的學習！！！

題目一：剪花布條

題目鏈接：剪花布條

【題目描述】

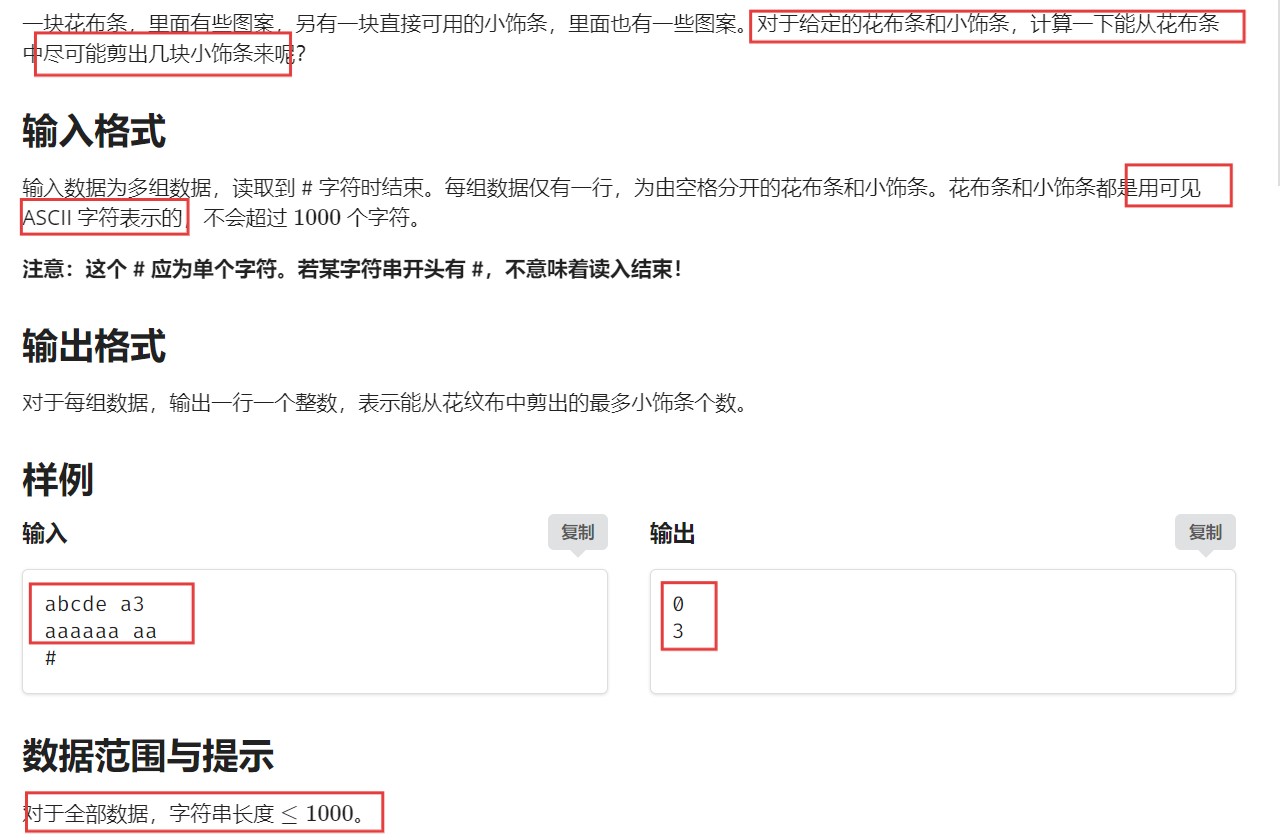
【算法原理】

這道題一眼就可以看出是字符串匹配的問題，暴力解法當然是拿著模式串去主串的每一個位置依次進行匹配，時間復雜度較高，但是這道題目數據范圍比較小，應該也是可以通過~~

這種字符串匹配的問題，我們可以嘗試使用 KMP 算法進行解決。

但不同于 KMP 算法模板題的是，這道題目找到所有匹配的位置之后，還要從左到右進行判斷篩選，不能重疊。這個只需要額外判斷匹配位置之間的距離是否大于模式串的長度就可以了。

注意：可見的 ASCII 字符是包括 ‘#’ 的，因此我們用 ‘ ’（空格）來鏈接模式串和主串。

【代碼實現】

#include <iostream>using namespace std;const int N = 2010; // 注意要開成兩倍 string s, t;
int n, m;
int pi[N];int main()
{while(cin >> s >> t){int ret = 0; n = s.size(); m = t.size();s = ' ' + t + ' ' + s;for(int i = 2; i <= m + n + 1; i++){int j = pi[i - 1];while(j && s[i] != s[j + 1]) j = pi[j];if(s[i] == s[j + 1]) j++;pi[i] = j;}for(int i = m + 1; i <= m + n + 1; i++){if(pi[i] == m){ret++;i += m - 1; // 出去以后還會 ++ 一次 // 防重疊 }}cout << ret << endl;}return 0;
}

題目二：Seek the Name

題目鏈接：Seek the Name

【題目描述】

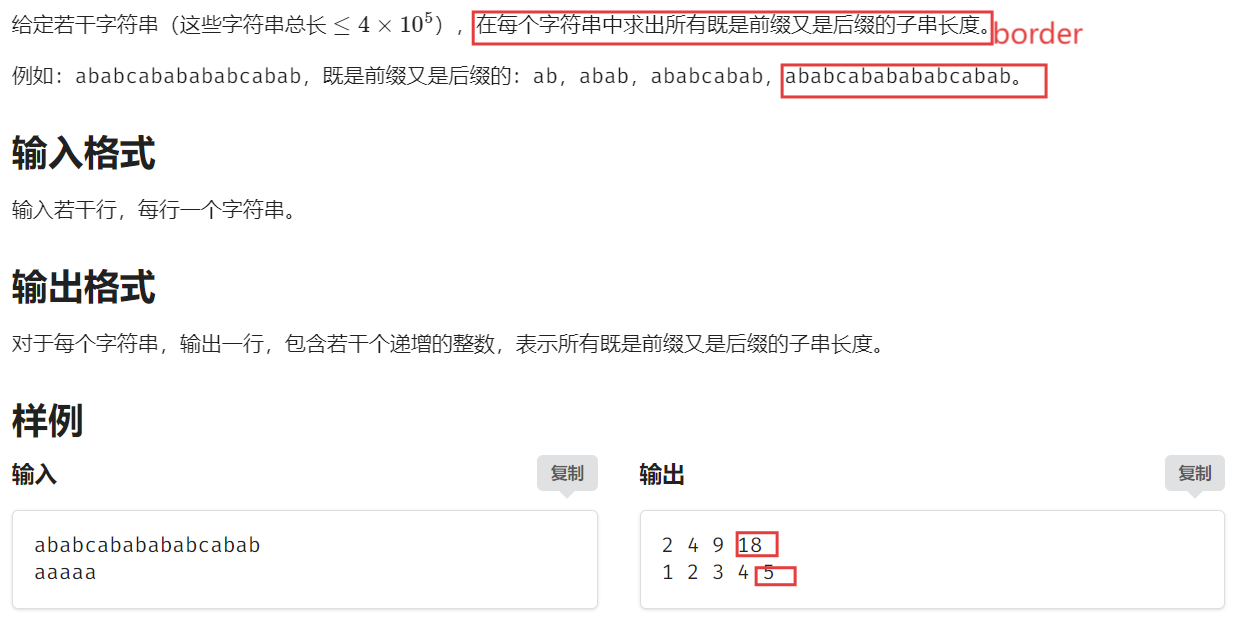
【算法原理】

前綴函數的小用途~~

border 的 border 還是 border

題目要求求出字符串所有 border 的長度，我們可以先求出最長的 border 的長度，再依次去找短的 border。這道題目就是一個簡單的求前綴函數的問題~~

用數組存儲所有 border 的長度，最后再逆序輸出。（有一種數組模擬棧的感覺）

最后不要忘記輸出整個字符串的長度~~，求 border 不會考慮，但是本題是要考慮的。

【代碼實現】

#include <iostream>using namespace std;const int N = 4e5 + 10;string s;
int n, pi[N];
int ret[N], top;int main()
{while(cin >> s){top = 0;n = s.size();s = ' ' + s;for(int i = 2; i <= n; i++){int j = pi[i - 1];while(j && s[i] != s[j + 1]) j = pi[j];if(s[i] == s[j + 1]) j++;pi[i] = j;}for(int i = pi[n]; i; i = pi[i]) ret[++top] = i;for(int i = top; i >= 1; i--) cout << ret[i] << " ";cout << n << endl;}return 0;
} 

題目三：ABB

題目鏈接 ABB

【題目描述】

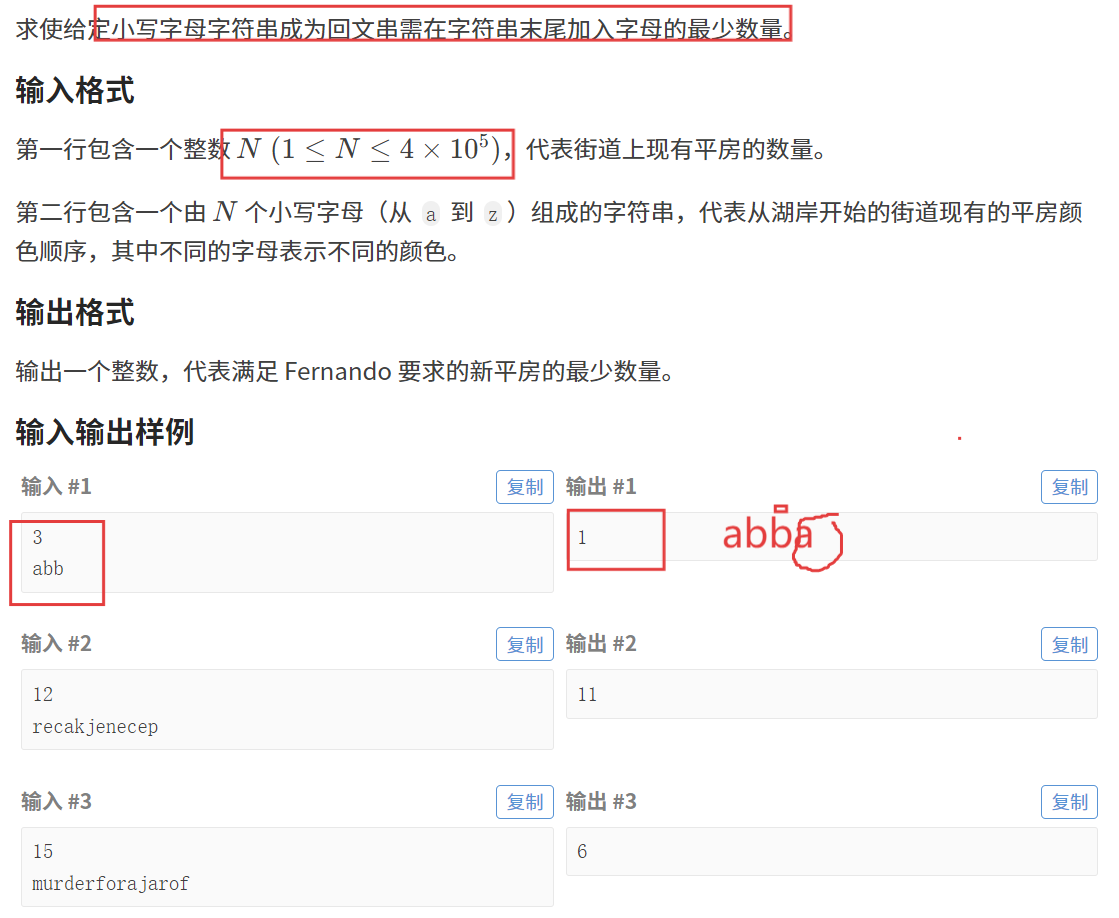
【算法原理】

對于回文串相關的問題，可以使用 malache 算法來解決，但是我們這個專題是 KMP，因此我們嘗試使用 KMP 算法來解決這個問題。

題目轉化：這道題實質上是求給定字符串的最長回文后綴的長度 len，n - len 就是最終結果。

因為題目要求你只能從字符串的末端去補充字符，所以回文后綴的長度越長，你要補充的字符數量就越少。

所以我們只需要解決求出一個字符串的最長回文后綴的長度就可以了~~

如何解決這個問題呢？？？

我們發現：如果將回文串逆序，應該和原始的字符串相同。因此，我們可以將字符串逆序之后拼接到原始字符串的前面，在中間加一個 ‘#’ 連接。

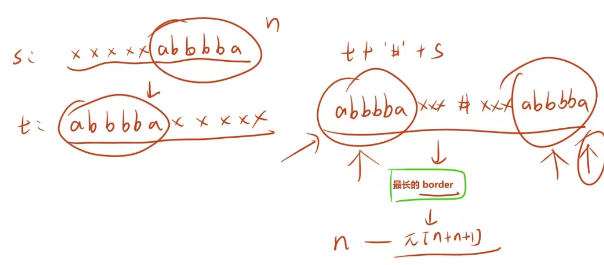
接下來，我們只需要求出新字符串最長的 border 長度 pi，再用 n - pi 就解決了。

【代碼實現】

#include <iostream>
#include <algorithm>using namespace std;const int N = 8e5 + 10; // 開兩倍 string s, t;
int n;
int pi[N];int main()
{cin >> n >> s;t = s;reverse(t.begin(), t.end());s = ' ' + t + '#' + s;for(int i = 2; i <= n + n + 1; i++){int j = pi[i - 1];while(j && s[i] != s[j + 1]) j = pi[j];if(s[i] == s[j + 1]) j++;pi[i] = j;}cout << n - pi[n + n + 1] << endl;return 0;
}

題目四：Censoring S

題目鏈接：Censoring S

【題目描述】

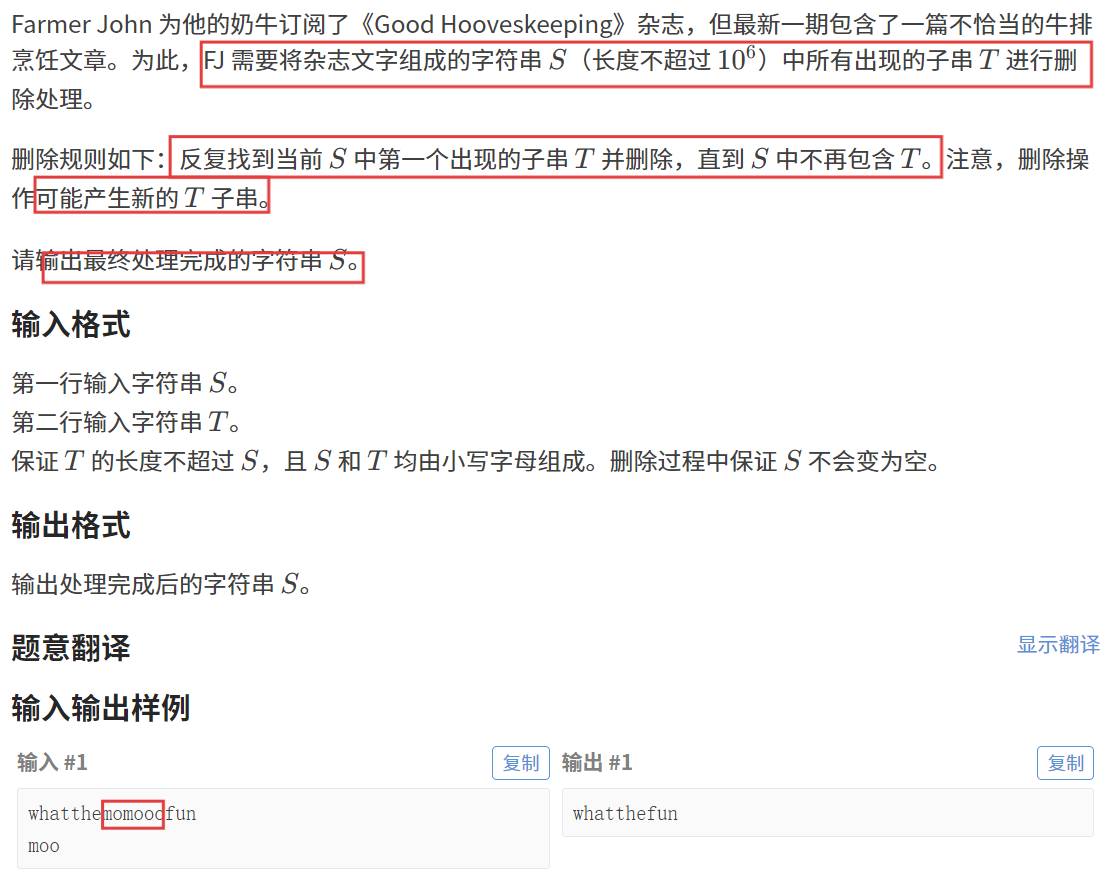
【算法原理】

KMP 算法 + 棧（存下標）

對于這種類似”消消樂“的玩法，我們很容易想到 “棧” 這樣的一個數據結構。

對于之前求前綴函數的模板，我們優先考慮使用【1，i - 1】的 border 來更新 【1，i】的 border

但是這道題目涉及消除的操作，因此我們不能使用【1，i - 1】的 border 來更新 【1，i】的 border（有可能前面的字符都消沒了）

而是使用棧頂下標的元素來更新【1，i】的 border。

【代碼實現】

#include <iostream>using namespace std;const int N = 2e6 + 10;string s, t;
int n, m, pi[N];
int st[N], top; // 用數組模擬棧 int main()
{cin >> s >> t;n = s.size(), m = t.size();s = ' ' + t + ' ' + s;// pi[1] = 0;st[++top] = 1;for(int i = 2; i <= n + m + 1; i++){int j = pi[st[top]];while(j && s[i] != s[j + 1]) j = pi[j];if(s[i] == s[j + 1]) j++;pi[i] = j;st[++top] = i;if(j == m){for(int k = 0; k < m; k++) top--;}}for(int i = m + 2; i <= top; i++) cout << s[st[i]];return 0;
}

好的，今天的分享到這里就結束了，謝謝大家！！！