提示：文章寫完后，目錄可以自動生成，如何生成可參考右邊的幫助文檔

---

前言

我們在刷題的時候會碰到各種各樣的《只出現一次的數字》的題目，在這里，我們對碰到的題目進行總結

一、給定一個整數數組nums，除了某個元素只出現一次以外，其余元素均出現兩次。找出那個只出現一次的元素

異或的性質：

• 0^x = x
• x^x = 0; 同樣的數異或兩次得到零
• 異或滿足交換律和結合律，不需要考慮順序

由于異或有以上的性質，所以我們可以將數組nums當中的元素依次進行異或操作，此時數組中出現兩次的數進行異或后變成了0，而最終異或得到的結果就是只出現一次的那個數

int* singleNumber(int* nums, int numsSize, int* returnSize)
{//找出這個值放到數組int* arr = (int*)malloc(sizeof(int)* 1);//輸出型參數，讓外面拿到數組的長度*returnSize =1 ;int ret = 0;for (int i = 0; i < numsSize; ++i){ret ^= nums[i];}arr[0] = ret;return arr;
}

二、給你一個整數數組nums，除某個元素僅出現一次外，其余每個元素都恰出現三次。請你找出并返回那個只出現了一次的元素

int類型變量的大小是4個字節，也就是32個比特位。由于相同的數的二進制序列都是一樣的，因此當我們遍歷nums數組當中的數字，依次同級每個比特位出現1的次數時，就會出現以下幾種情況：

• 某一比特位出現1的次數為0，表明數組nums當中的所有數字的該比特位都為0，因此只出現一次的數字的該比特位也為0
• 某一比特位出現1的次數對3取余后得到0值，表明數組nums中只出現一次的數字的該比特位為0
• 某一比特位出現1的次數為3取余后得到非0值，表明數字nums中只出現一次的數字的該比特位為1

因此當我們遍歷nums數組統計得到每個比特位出現1的次數之后，就可以將這32個值依次對3進行求余操作，最終得到的32個0/1序列就是只出現一次的數字的二進制序列

#include <stdio.h>
#include <stdlib.h>
int singleNumber(int* nums, int numsSize) 
{int ret = 0; // 初始化結果為0// 遍歷整數的32個比特位for (int i = 0; i < 32; i++){int total = 0; // 用于統計當前比特位為1的元素個數// 遍歷數組中的所有元素for (int j = 0; j < numsSize; j++) {// 將當前元素右移i位，然后與1進行與操作// 這樣可以提取出第i個比特位的值（0或1）total += ((nums[j] >> i) & 1);}// 如果第i個比特位為1的元素個數不能被3整除// 則說明只出現一次的數字的這一比特位為1if (total % 3 != 0){// 使用位或操作將ret的第i個比特位設置為1ret |= (1 << i);}}return ret; // 返回只出現一次的數字
}// 示例使用
int main() {int nums[] = {2, 2, 3, 2}; // 示例數組，3是只出現一次的數字int size = sizeof(nums) / sizeof(nums[0]);int result = singleNumber(nums, size);printf("只出現一次的數字是: %d\n", result); // 應該輸出3return 0;
}

我們也可以使用排序后遍歷的方法，不過與位操作方法相比，位操作的時間復雜度為O(n)，空間復雜度為O(1)；排序后遍歷的方法其復雜度為O(nlongn)，空間復雜度為O(1)或O(n)，但是其實現簡單

使用數組排序后遍歷

#include <stdio.h>
#include <stdlib.h>// 比較函數，用于qsort
int compare(const void* a, const void* b) {return (*(int*)a - *(int*)b);
}int singleNumber(int* nums, int numsSize) {// 先對數組進行排序qsort(nums, numsSize, sizeof(int), compare);// 遍歷排序后的數組for (int i = 0; i < numsSize; i += 3) {// 如果當前元素與下一個元素不同，或者已經到達數組末尾if (i == numsSize - 1 || nums[i] != nums[i + 1]) {return nums[i];}}return -1; // 如果沒有找到，返回-1
}

三、一個整型數組nums里除了兩個數字之外，其他數字都出現了兩次，請找出這兩個只出現一次的數字。要求時間復雜度為O(n)，空間復雜度是O(1)

數組nums當中除了出現一次的數字之外，剩下的都是出現兩次的數字，但是我們不能直接遍歷數組元素進行異或操作，因為此時nums數組當中有兩個出現一次的數字，如果我們直接將所有數字進行異或，最終得到的實際就是這兩個出現一次的數字相異或后的結果

如果我們可以將數組nums當中的數字分為兩組，并且這兩個出現一次的數字正好分別分到了兩組，此時就相當于分別在這兩個小組中找出現一次的數字，問題就回到了第一題

現在的問題就變成了，如何將這兩個只出現一次的數字分到兩個不同的組別中。
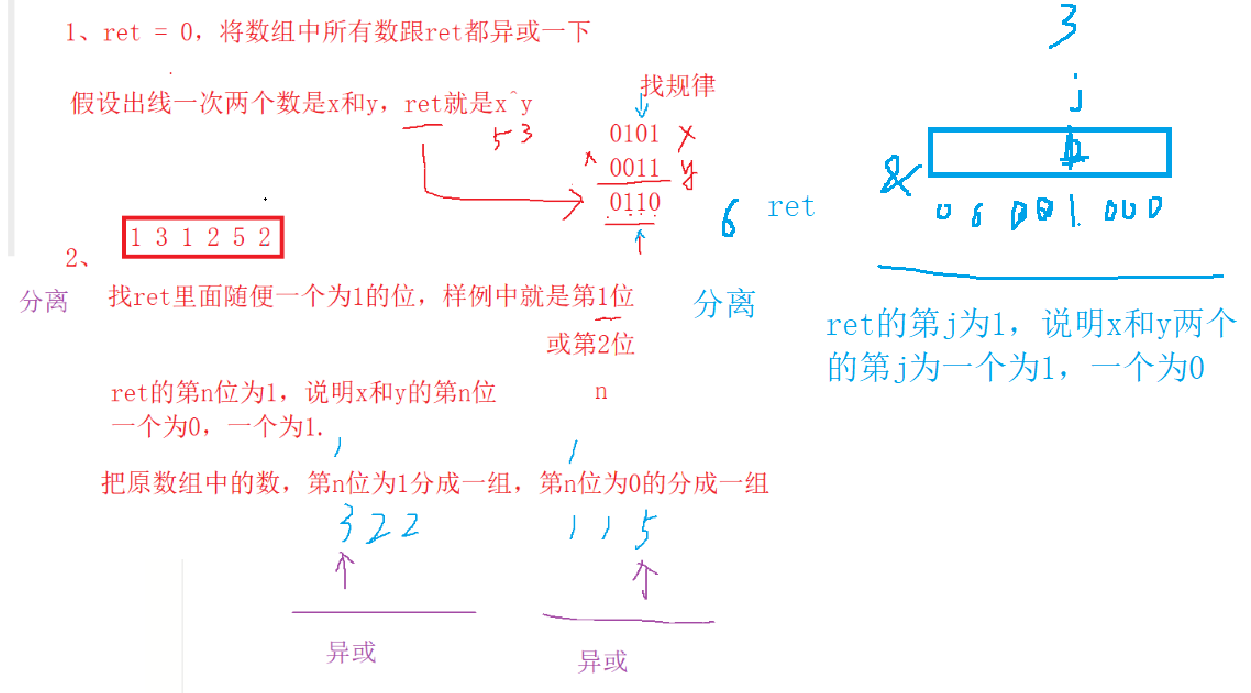
這個實際上很簡單，因為我們直接對數組nums當中的元素進行異或操作，得到的實際上就是這兩個只出現一次的數字相異或的結果，我們將結果稱為ret。由于這兩個只出現一次的數字的二進制序列是不同的，因此在ret的二進制序列當中一定至少存在一個不為0的比特位，而這兩個只出現一次的數字的該比特位的值是不同的，一個為0，一個為1
因此我們可以根據該比特位來進行分組，將數組nums當中該比特位為1的數字分為一組，將該比特位為0的數字分到另一組，則這兩個只出現一次的數字就一定被分到了兩個不同的組當中，其他出現兩次的數字，要么在這一組，要么在另一組

解題步驟如下：

1. 遍歷數組nums，對數組中的所有元素進行異或，得到異或后的結果ret
2. 找出ret當中任意一個不為0的比特位記為j
3. 將原數組分為兩組，第j位為1的為a組，第j位為0的為b組
4. x和y一定會分別進入a、b組，其他出現兩次的數，要么進入a組，要么進入b組
5. a組和b組數據就變成其他數出現2次，只有一個數出現1次
6. 再對a、b組進行異或就可以找出x和y

int* singleNumber(int* nums, int numsSize, int* returnSize)
{   //1.計算所有元素的異或結果int ret = 0;for (int i = 0; i < numsSize; i++){ret ^= nums[i];}//2.找到ret中為1的任意一位(即x和y不同的位)int j = 0;while (((ret >> j) & 1) == 0){j++;}//3.根據第j位將數組分為兩組，并分別計算異或int x = 0, y = 0;for (int k = 0; k < numsSize; k++){if ((nums[k] >> j) & 1){x ^= nums[k];}else{y ^= nums[k];}}//4.準備返回值int* arr = (int*)malloc(sizeof(int)* 2);arr[0] = x;arr[1] = y;*returnSize = 2;return arr;
}

四、給定一個整數數組nums和一個整數k，除了某個元素僅出現一次外，其余每個元素都恰好出現了k次，請你找出并返回那個只出現了一次的元素

數組中除了那個只出現一次的數字之外，無論其他數字出現多少次，我們實際都可以通過統計每個比特位出現1的次數的方式進行求解
只不過現在我們是將得到的32個比特位各自出現1的次數對k進行求余操作，最終得到的32個0/1序列也就是出現一次的數字的二進制序列

#include <stdio.h>
#include <stdlib.h>
int singleNumber(int* nums, int numsSize,int k)
{int ret = 0; // 初始化結果為0// 遍歷整數的32個比特位for (int i = 0; i < 32; i++){int total = 0; // 用于統計當前比特位為1的元素個數// 遍歷數組中的所有元素for (int j = 0; j < numsSize; j++){// 將當前元素右移i位，然后與1進行與操作// 這樣可以提取出第i個比特位的值（0或1）total += ((nums[j] >> i) & 1);}// 如果第i個比特位為1的元素個數不能被k整除// 則說明只出現一次的數字的這一比特位為1if (total % k != 0){// 使用位或操作將ret的第i個比特位設置為1ret |= (1 << i);}}return ret; // 返回只出現一次的數字
}// 示例使用
int main() {int nums[] = { 2, 2, 3, 2 }; // 示例數組，3是只出現一次的數字int size = sizeof(nums) / sizeof(nums[0]);int k = 3;int result = singleNumber(nums, size,k);printf("只出現一次的數字是: %d\n", result); // 應該輸出3return 0;
}