視頻講解：https://www.bilibili.com/video/BV1KT4y1M7HJ/?vd_source=a935eaede74a204ec74fd041b917810c
文檔講解：https://programmercarl.com/0039.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8C.html#%E6%80%9D%E8%B7%AF
力扣題目：https://leetcode.cn/problems/combination-sum/

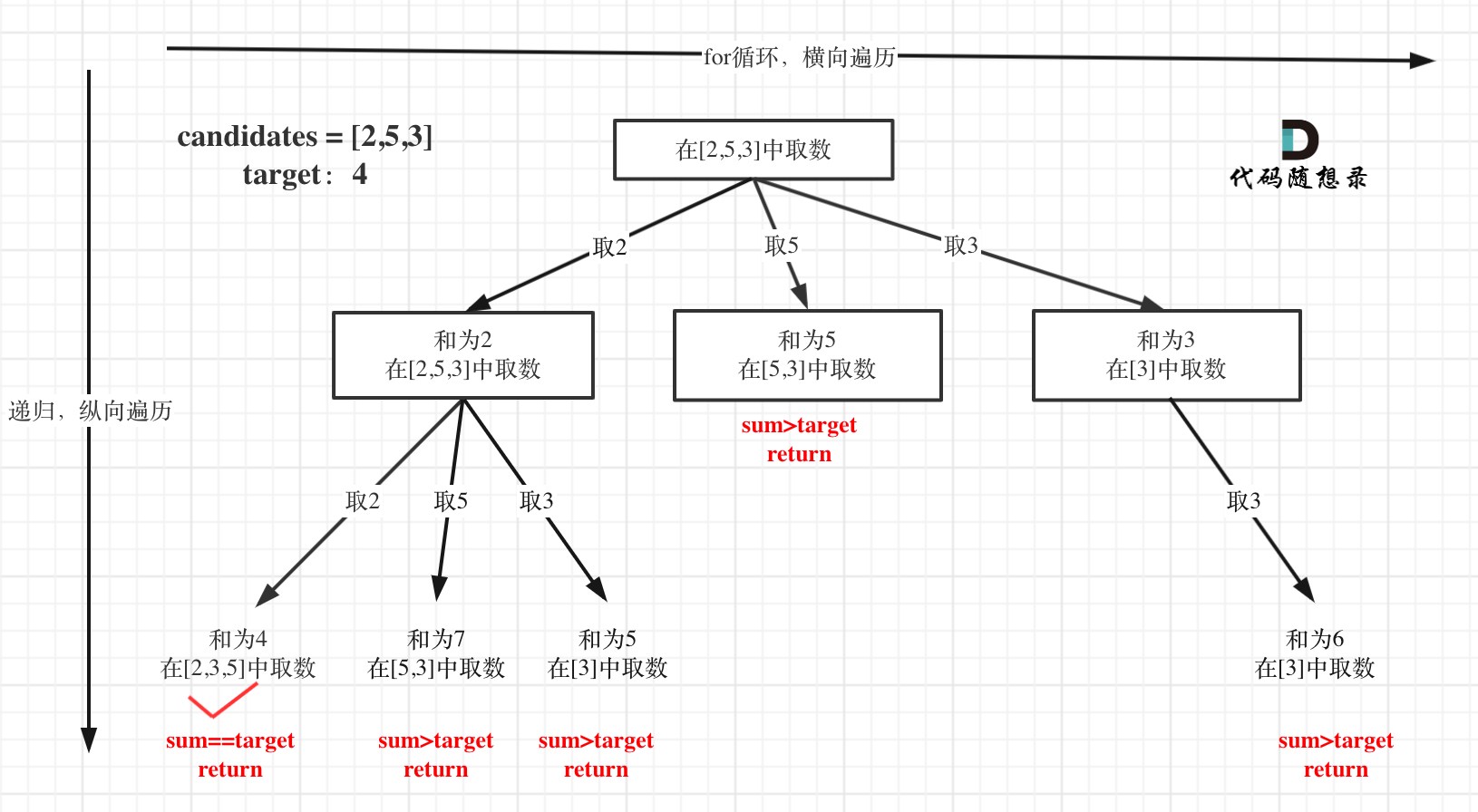
在這道題中，有幾個難點，1.數組元素可以重復選擇 2.返回結果不能有重復
因此這就帶來一定的困難，所以我們要注意以下幾點：

1. 可以重復選擇的話，選擇一個元素后剩下的選擇仍然是數組的全部
2. 返回結果不能有重復的話，我們不會再往前去遍歷元素
   因此在深入樹的過程中，我們可選的范圍是當前元素之后的所有元素（包含當前元素），如選擇2后，可選范圍為253，選擇5后可選范圍為53，選擇3后，可選范圍為3。
   還有一個注意的點就是剪枝，可以提升效率，我們可以把數組排列成有序的數組，如果在回溯過程中sum和大于target，那么這一層以及之后的都不用看了，肯定大于target，直接return就好。

class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex){//判斷終止條件if(sum > target) return;if(sum == target){result.push_back(path);return;}//開始遍歷for(int i = startIndex; i<candidates.size(); i++){//計算sumsum = sum + candidates[i];if(sum > target) return;//存入路徑path.push_back(candidates[i]);//回溯遍歷,因為從該路徑自身到結尾可以繼續遍歷，所以從i開始回溯遍歷backtracking(candidates, target, sum, i);//回溯完成，還原sum，彈出pathsum = sum - candidates[i];path.pop_back();}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {//初始化數組result.clear();path.clear();//排序數組sort(candidates.begin(), candidates.end());backtracking(candidates, target, 0, 0);return result;}
};