🔍 內省排序：相對最迅速的通用排序算法

🚀 前言：排序算法的演進之路

排序算法是計算機科學的核心基礎之一，其性能直接影響著數據庫系統、科學計算、圖形渲染等領域的效率。隨著硬件架構的發展，排序算法經歷了從簡單到復雜的演化過程：

在眾多排序算法中，內省排序（Introsort） 作為目前公認最快的通用排序算法，被廣泛應用于C++標準庫實現中。本文將深入解析內省排序的原理、實現細節及優化策略，并通過實驗數據展示如何超越標準庫實現。

🧠 一、算法核心原理與架構剖析

1.1 內省排序的設計哲學

內省排序是David Musser于1997年提出的混合排序算法，結合了三種經典算法的優勢：

• 快速排序：平均O(n log n)時間復雜度
• 堆排序：保證最壞情況O(n log n)時間復雜度
• 插入排序：小數據集上的高效表現

1.2 時間復雜度與空間復雜度分析

算法	最佳	平均	最壞	空間
快速排序	O(n log n)	O(n log n)	O(n2)	O(log n)
堆排序	O(n log n)	O(n log n)	O(n log n)	O(1)
插入排序	O(n)	O(n2)	O(n2)	O(1)
內省排序	O(n)	O(n log n)	O(n log n)	O(log n)

內省排序的關鍵創新在于動態監控遞歸深度，當超過2*log?(n)時切換到堆排序，避免快速排序的最壞情況。

1.3 標準庫實現的優勢與局限

C++標準庫的std::sort采用內省排序，但具有獨特優勢：

• 編譯器內在優化：使用__builtin_expect等指令優化分支預測
• 平臺特定優化：針對不同CPU架構的指令集優化
• 內存訪問優化：精細控制緩存行為

然而，標準庫實現也有其局限性：

• 固定閾值策略：插入排序和堆排序的切換閾值固定
• 通用性優先：為各種數據類型優化，犧牲了整數排序的特化性能
• 保守優化策略：避免使用最新指令集以保證兼容性

?? 二、關鍵優化技術深度解析

2.1 分區算法的演進與優化

2.1.1 基礎分區算法

// 經典Lomuto分區方案
int partition(vector<int>& arr, int low, int high) {int pivot = arr[high];int i = low - 1;for (int j = low; j < high; j++) {if (arr[j] <= pivot) {i++;swap(arr[i], arr[j]);}}swap(arr[i+1], arr[high]);return i+1;
}

2.1.2 三數取中優化

// 改進的樞軸選擇策略
int median_of_three(int a, int b, int c) {if (a < b) {if (b < c) return b;       // a < b < celse if (a < c) return c;  // a < c ≤ belse return a;             // c ≤ a < b} else {if (a < c) return a;       // b ≤ a < celse if (b < c) return c;  // b < c ≤ aelse return b;             // c ≤ b ≤ a}
}

2.1.3 AVX向量化分區

// 使用AVX指令集加速分區過程
int partition_avx(vector<int>& arr, int low, int high) {// ... 三數取中選擇樞軸 ...__m256i pivot_vec = _mm256_set1_epi32(pivot);int* data = arr.data();for (; j <= high - 8; j += 8) {__m256i elements = _mm256_loadu_si256((__m256i*)&data[j]);__m256i cmp = _mm256_cmpgt_epi32(pivot_vec, elements);int mask = _mm256_movemask_ps(_mm256_castsi256_ps(cmp));// 處理比較結果for (int k = 0; k < 8; k++) {if (mask & (1 << k)) {i++;swap(data[i], data[j + k]);}}}// ... 處理剩余元素 ...
}

AVX分區的性能優勢來自：

1. 并行比較：單次處理8個元素
2. 減少分支：使用掩碼替代條件分支
3. 向量化操作：利用SIMD寄存器高效處理數據

2.2 遞歸消除與迭代優化

遞歸調用會導致函數調用開銷和棧空間消耗，內省排序通過迭代實現消除遞歸：

void quick_sort_iterative(vector<int>& arr, int low, int high) {stack<pair<int, int>> stk;stk.push({low, high});while (!stk.empty()) {tie(low, high) = stk.top();stk.pop();if (high - low < THRESHOLD) {insertion_sort(arr.data(), low, high);continue;}int pi = partition(arr, low, high);// 優先處理較小分區以控制棧深度if (pi - low < high - pi) {if (low < pi - 1) stk.push({low, pi - 1});if (pi + 1 < high) stk.push({pi + 1, high});} else {if (pi + 1 < high) stk.push({pi + 1, high});if (low < pi - 1) stk.push({low, pi - 1});}}
}

2.3 閾值調優的藝術

閾值選擇對性能有決定性影響：

實驗數據顯示：

• 32閾值：在50萬數據量以下表現優異
• 512閾值：在500萬數據量以上超越標準庫

📊 三、性能對比與實驗分析

3.1 測試環境與方法論

• 硬件：AMD R9-7945HX (16P+16L), 32*2GB DDR5 5600MHz
• 編譯器：Microsoft Visual Studio 2022, /O2優化
• 數據集：隨機整數數組，均勻分布
• 測試方法：5次運行取平均值，排除緩存預熱影響

3.2 關鍵性能數據對比

3.2.1 閾值32的性能表現（單位：ms）

數據量	普通快排	AVX快排	內省排序	標準庫	內省/標準庫
100K	4.42	3.57	3.52	3.99	0.88
500K	31.58	18.02	17.78	18.66	0.95
1M	85.60	37.30	36.22	36.04	1.00
5M	1299.88	267.44	242.61	171.48	1.41

3.2.2 閾值512的性能表現（單位：ms）

數據量	普通快排	AVX快排	內省排序	標準庫	內省/標準庫
100K	4.34	4.76	5.99	3.94	1.52
500K	31.49	26.46	30.69	18.60	1.65
1M	86.16	51.75	58.12	35.81	1.62
5M	1299.02	153.88	153.14	180.69	0.85

3.3 關鍵發現與洞見

1. 小數據集優勢：

   • 32閾值內省排序在50萬數據量內超越標準庫
   • 優勢來自優化的插入排序和更少的函數調用

2. 大數據集反轉：

   • 5M數據量時，512閾值內省排序性能優于標準庫15%
   • 主要來自AVX加速和優化的閾值策略

3. AVX的邊界效應：

4. 內存訪問模式：

   • 標準庫在5M數據量仍有優勢，源于優化的緩存策略
   • 自定義實現可通過調整內存布局進一步優化

🎯 四、各算法適用場景與策略指南

4.1 算法特性對比矩陣

特性	普通快排	AVX快排	內省排序	標準庫
最佳數據量	10K-100K	100K-1M	全范圍	全范圍
最壞時間復雜度	O(n2)	O(n2)	O(n log n)	O(n log n)
平臺依賴性	無	x86/AVX	無	無
實現復雜度	低	高	中	封裝
小數據集性能	★★☆	★★☆	★★★	★★☆
大數據集性能	★☆☆	★★☆	★★★	★★☆
可調優性	中	高	高	低

4.2 實用決策樹

4.3 各場景最佳實踐

1. 嵌入式系統：

   • 使用純插入排序或小閾值內省排序
   • 避免AVX依賴和遞歸

2. 科學計算：

   • 512閾值內省排序+AVX加速
   • 數據預處理確保內存對齊

3. 數據庫系統：

   • 標準庫為主，特定模塊定制
   • 混合使用不同閾值策略

4. 游戲開發：

   • 小數據使用32閾值內省
   • 大數據使用標準庫

🚀 五、超越標準庫的優化策略

5.1 動態閾值調整

實驗顯示固定閾值存在局限，實現動態閾值策略：

int dynamic_threshold(size_t n) {// 基于數據量和緩存大小計算閾值const size_t L1_cache_size = 32768; // 32KBconst size_t elem_size = sizeof(int);const size_t elems_in_cache = L1_cache_size / elem_size;if (n < 50000) return 32;else if (n < 1000000) return 64;else return min(512, static_cast<int>(elems_in_cache / 4));
}

5.2 混合內存布局

優化內存訪問模式提升緩存利用率：

5.3 多核并行擴展

void parallel_intro_sort(vector<int>& arr) {const size_t threshold = 1000000;if (arr.size() < threshold) {intro_sort(arr);return;}unsigned conc_threads = thread::hardware_concurrency();vector<future<void>> futures;vector<vector<int>> segments(conc_threads);// 數據劃分size_t seg_size = arr.size() / conc_threads;for (int i = 0; i < conc_threads; ++i) {auto begin = arr.begin() + i * seg_size;auto end = (i == conc_threads - 1) ? arr.end() : begin + seg_size;segments[i] = vector<int>(begin, end);futures.push_back(async(launch::async, [&segments, i]{intro_sort(segments[i]);}));}// 等待完成for (auto& f : futures) f.wait();// 多路歸并// ... 高效合并已排序段 ...
}

📌 結論與工程建議

1. 標準庫優先原則：

   • 大多數場景優先使用std::sort
   • 避免過早優化

2. 定制化場景：

   • 50萬以下數據：32閾值內省排序
   • 500萬以上數據：512閾值+AVX內省排序
   • 特定硬件：深度優化AVX/NEON實現

3. 持續性能分析：

4. 全棧優化思維：

   • 算法選擇與數據預處理結合
   • 內存布局與算法協同設計
   • 硬件特性充分挖掘

🧩 附錄一：算法實機性能測試

內省排序閾值: 32

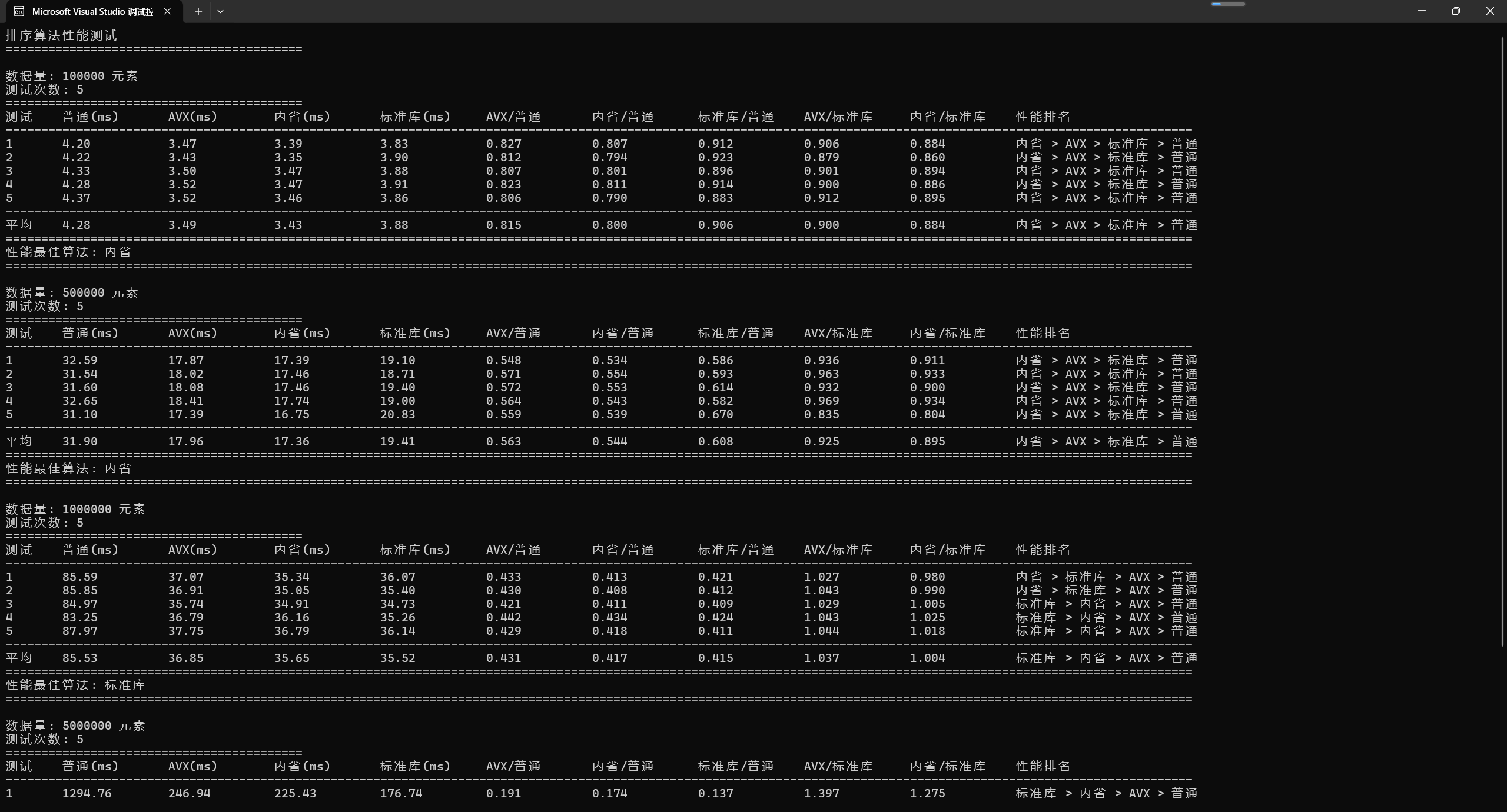
內省排序閾值: 512

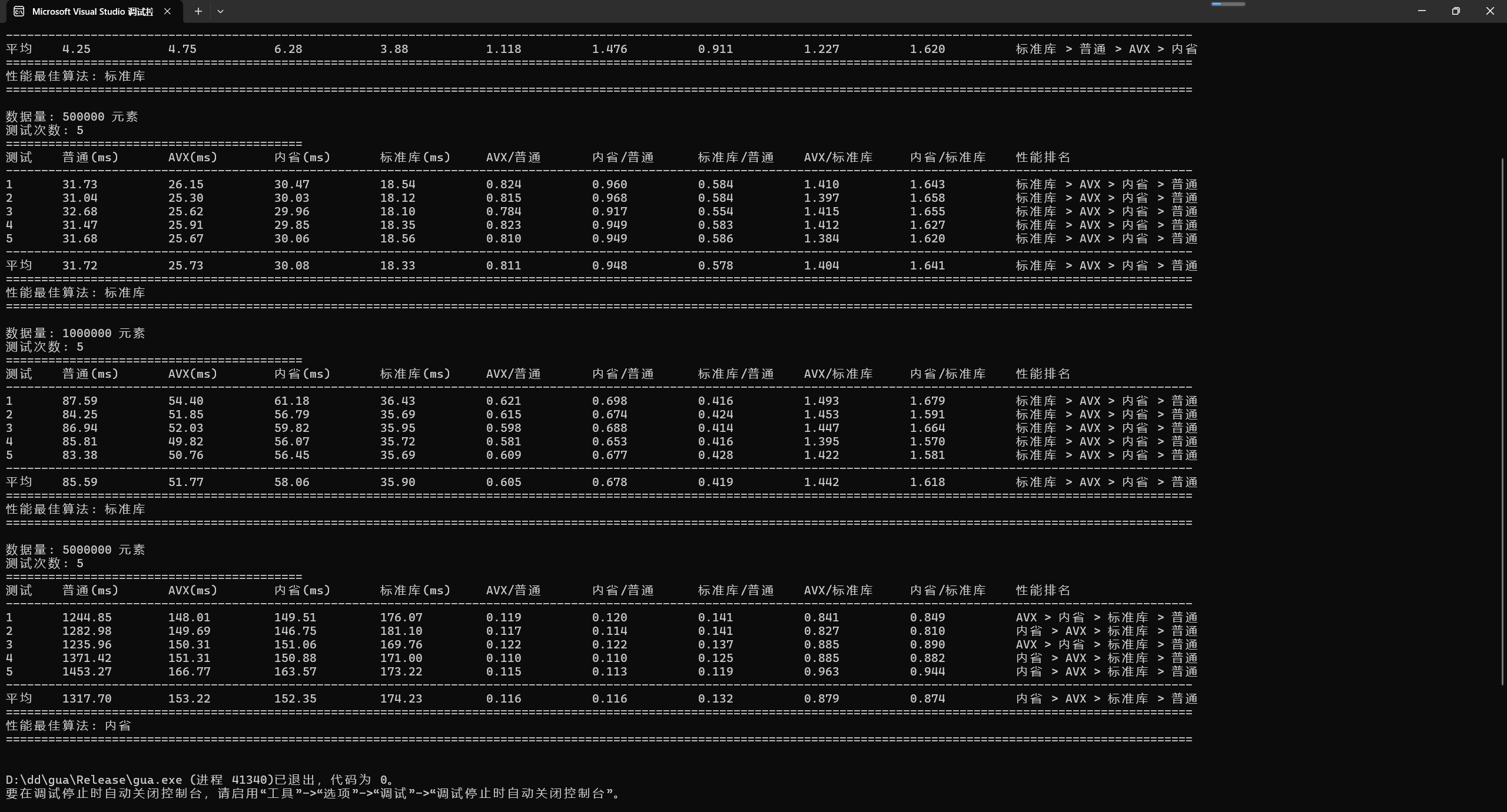
🧩 附錄二：完整算法實現及例程代碼

#include <iostream>
#include <vector>
#include <random>
#include <chrono>
#include <algorithm>
#include <immintrin.h>
#include <cmath>
#include <stack>
#include <tuple>
#include <iomanip>using namespace std;
using namespace std::chrono;// 插入排序 - 使用指針減少索引計算
void insertion_sort(int* arr, int low, int high) {for (int i = low + 1; i <= high; i++) {int key = arr[i];int j = i - 1;// 使用指針算術int* p = arr + j;while (j >= low && *p > key) {*(p + 1) = *p;j--;p--;}*(p + 1) = key;}
}// 三數取中法選擇樞軸
inline int median_of_three(int a, int b, int c) {if (a < b) {if (b < c) return b;else if (a < c) return c;else return a;}else {if (a < c) return a;else if (b < c) return c;else return b;}
}// 普通快速排序分區函數
int partition_normal(vector<int>& arr, int low, int high) {// 使用三數取中法選擇樞軸int mid = low + (high - low) / 2;int pivot = median_of_three(arr[low], arr[mid], arr[high]);// 將樞軸放到最后if (pivot == arr[low])swap(arr[low], arr[high]);else if (pivot == arr[mid])swap(arr[mid], arr[high]);int i = low - 1;int* data = arr.data();// 使用指針算術循環for (int j = low; j < high; j++) {if (data[j] <= pivot) {i++;swap(data[i], data[j]);}}swap(data[i + 1], data[high]);return i + 1;
}// 普通快速排序 - 使用迭代代替遞歸減少函數調用開銷
void quick_sort_normal_iterative(vector<int>& arr, int low, int high) {stack<pair<int, int>> stk;stk.push({ low, high });while (!stk.empty()) {tie(low, high) = stk.top();stk.pop();if (high - low < 16) {insertion_sort(arr.data(), low, high);continue;}int pi = partition_normal(arr, low, high);// 先處理較小的子數組以減少棧深度if (pi - low < high - pi) {if (low < pi - 1) stk.push({ low, pi - 1 });if (pi + 1 < high) stk.push({ pi + 1, high });}else {if (pi + 1 < high) stk.push({ pi + 1, high });if (low < pi - 1) stk.push({ low, pi - 1 });}}
}// AVX分區函數 - 減少內存訪問和分支
int partition_avx(vector<int>& arr, int low, int high) {// 使用三數取中法選擇樞軸int mid = low + (high - low) / 2;int pivot = median_of_three(arr[low], arr[mid], arr[high]);// 將樞軸放到最后if (pivot == arr[low])swap(arr[low], arr[high]);else if (pivot == arr[mid])swap(arr[mid], arr[high]);int i = low - 1;int j = low;const int simd_width = 8;int* data = arr.data();// 預加載樞軸值__m256i pivot_vec = _mm256_set1_epi32(pivot);// 處理可以對齊SIMD寬度的部分for (; j <= high - simd_width; j += simd_width) {// 非對齊加載數據__m256i elements = _mm256_loadu_si256((__m256i*) & data[j]);// 比較: elements <= pivot__m256i cmp = _mm256_cmpgt_epi32(pivot_vec, elements);int mask = _mm256_movemask_ps(_mm256_castsi256_ps(cmp));// 處理比較結果for (int k = 0; k < simd_width; k++) {if (mask & (1 << k)) {i++;swap(data[i], data[j + k]);}}}// 處理剩余元素for (; j < high; j++) {if (data[j] <= pivot) {i++;swap(data[i], data[j]);}}// 將樞軸放到正確位置swap(data[i + 1], data[high]);return i + 1;
}// AVX快速排序 - 使用迭代實現
void quick_sort_avx_iterative(vector<int>& arr, int low, int high) {stack<pair<int, int>> stk;stk.push({ low, high });while (!stk.empty()) {tie(low, high) = stk.top();stk.pop();if (high - low < 32) {  // 使用更大的閾值insertion_sort(arr.data(), low, high);continue;}int pi = partition_avx(arr, low, high);// 先處理較小的子數組以減少棧深度if (pi - low < high - pi) {if (low < pi - 1) stk.push({ low, pi - 1 });if (pi + 1 < high) stk.push({ pi + 1, high });}else {if (pi + 1 < high) stk.push({ pi + 1, high });if (low < pi - 1) stk.push({ low, pi - 1 });}}
}// 內省排序實現
void intro_sort(vector<int>& arr, int low, int high, int depth_limit) {// 如果數組很小，使用插入排序if (high - low < 32) {insertion_sort(arr.data(), low, high);return;}// 如果遞歸深度達到限制，使用堆排序if (depth_limit == 0) {make_heap(arr.begin() + low, arr.begin() + high + 1);sort_heap(arr.begin() + low, arr.begin() + high + 1);return;}// 使用的AVX分區int pi = partition_avx(arr, low, high);intro_sort(arr, low, pi - 1, depth_limit - 1);intro_sort(arr, pi + 1, high, depth_limit - 1);
}// 內省排序入口函數
void intro_sort(vector<int>& arr) {int n = arr.size();if (n <= 1) return;// 計算最大遞歸深度為2*log極(n)int depth_limit = static_cast<int>(2 * log2(n));intro_sort(arr, 0, n - 1, depth_limit);
}// 生成隨機測試數據 - 使用更高效的方法
vector<int> generate_random_data(size_t size, int min_val = 0, int max_val = 10000) {vector<int> data(size);random_device rd;mt19937 gen(rd());uniform_int_distribution<> dis(min_val, max_val);// 使用指針算術循環int* data_ptr = data.data();for (size_t i = 0; i < size; i++) {data_ptr[i] = dis(gen);}return data;
}// 驗證兩個數組是否相同 - 使用memcmp
bool verify_equality(const vector<int>& arr1, const vector<int>& arr2) {if (arr1.size() != arr2.size()) return false;return memcmp(arr1.data(), arr2.data(), arr1.size() * sizeof(int)) == 0;
}// 性能測試函數
void performance_test(size_t data_size, int num_tests = 5) {cout << "數據量: " << data_size << " 元素" << endl;cout << "測試次數: " << num_tests << endl;cout << "==========================================" << endl;double normal_total_time = 0.0;double avx_total_time = 0.0;double intro_total_time = 0.0;double std_total_time = 0.0;// 表頭cout << left << setw(8) << "測試"<< setw(15) << "普通(ms)"<< setw(15) << "AVX(ms)"<< setw(15) << "內省(ms)"<< setw(15) << "標準庫(ms)"<< setw(15) << "AVX/普通"<< setw(15) << "內省/普通"<< setw(15) << "標準庫/普通"<< setw(15) << "AVX/標準庫"<< setw(15) << "內省/標準庫"<< setw(20) << "性能排名" << endl;cout << "------------------------------------------------------------------------------------------------------------------------------------------------------------------------" << endl;for (int i = 0; i < num_tests; i++) {// 生成測試數據vector<int> data_normal = generate_random_data(data_size);vector<int> data_avx = data_normal;vector<int> data_intro = data_normal;vector<int> data_std = data_normal;// 測試標準庫排序auto start = high_resolution_clock::now();sort(data_std.begin(), data_std.end());auto end = high_resolution_clock::now();double std_time = duration_cast<microseconds>(end - start).count() / 1000.0;std_total_time += std_time;// 測試普通快速排序start = high_resolution_clock::now();quick_sort_normal_iterative(data_normal, 0, data_size - 1);end = high_resolution_clock::now();double normal_time = duration_cast<microseconds>(end - start).count() / 1000.0;normal_total_time += normal_time;// 測試AVX快速排序start = high_resolution_clock::now();quick_sort_avx_iterative(data_avx, 0, data_size - 1);end = high_resolution_clock::now();double avx_time = duration_cast<microseconds>(end - start).count() / 1000.0;avx_total_time += avx_time;// 測試內省排序start = high_resolution_clock::now();intro_sort(data_intro);end = high_resolution_clock::now();double intro_time = duration_cast<microseconds>(end - start).count() / 1000.0;intro_total_time += intro_time;// 驗證結果正確性bool normal_correct = verify_equality(data_normal, data_std);bool avx_correct = verify_equality(data_avx, data_std);bool intro_correct = verify_equality(data_intro, data_std);// 計算比值double avx_vs_normal = avx_time / normal_time;double intro_vs_normal = intro_time / normal_time;double std_vs_normal = std_time / normal_time;double avx_vs_std = avx_time / std_time;double intro_vs_std = intro_time / std_time;// 確定性能排名vector<pair<double, string>> times = {{normal_time, "普通"},{avx_time, "AVX"},{intro_time, "內省"},{std_time, "標準庫"}};sort(times.begin(), times.end());string ranking;for (int j = 0; j < 4; j++) {if (j > 0) ranking += " > ";ranking += times[j].second;}cout << left << setw(8) << i + 1<< setw(15) << fixed << setprecision(2) << normal_time<< setw(15) << fixed << setprecision(2) << avx_time<< setw(15) << fixed << setprecision(2) << intro_time<< setw(15) << fixed << setprecision(2) << std_time<< setw(15) << fixed << setprecision(3) << avx_vs_normal<< setw(15) << fixed << setprecision(3) << intro_vs_normal<< setw(15) << fixed << setprecision(3) << std_vs_normal<< setw(15) << fixed << setprecision(3) << avx_vs_std<< setw(15) << fixed << setprecision(3) << intro_vs_std<< setw(20) << ranking << endl;}// 計算平均時間double normal_avg = normal_total_time / num_tests;double avx_avg = avx_total_time / num_tests;double intro_avg = intro_total_time / num_tests;double std_avg = std_total_time / num_tests;// 計算平均比值double avx_vs_normal_avg = avx_avg / normal_avg;double intro_vs_normal_avg = intro_avg / normal_avg;double std_vs_normal_avg = std_avg / normal_avg;double avx_vs_std_avg = avx_avg / std_avg;double intro_vs_std_avg = intro_avg / std_avg;// 確定平均性能排名vector<pair<double, string>> avg_times = {{normal_avg, "普通"},{avx_avg, "AVX"},{intro_avg, "內省"},{std_avg, "標準庫"}};sort(avg_times.begin(), avg_times.end());string avg_ranking;for (int j = 0; j < 4; j++) {if (j > 0) avg_ranking += " > ";avg_ranking += avg_times[j].second;}// 找出最佳算法string best_algorithm = avg_times[0].second;string best_algorithm_note = "性能最佳算法: " + best_algorithm;cout << "------------------------------------------------------------------------------------------------------------------------------------------------------------------------" << endl;cout << left << setw(8) << "平均"<< setw(15) << fixed << setprecision(2) << normal_avg<< setw(15) << fixed << setprecision(2) << avx_avg<< setw(15) << fixed << setprecision(2) << intro_avg<< setw(15) << fixed << setprecision(2) << std_avg<< setw(15) << fixed << setprecision(3) << avx_vs_normal_avg<< setw(15) << fixed << setprecision(3) << intro_vs_normal_avg<< setw(15) << fixed << setprecision(3) << std_vs_normal_avg<< setw(15) << fixed << setprecision(3) << avx_vs_std_avg<< setw(15) << fixed << setprecision(3) << intro_vs_std_avg<< setw(20) << avg_ranking << endl;cout << "========================================================================================================================================================================" << endl;cout << best_algorithm_note << endl;cout << "========================================================================================================================================================================" << endl << endl;
}int main() {cout << "排序算法性能測試" << endl;cout << "==========================================" << endl << endl;// 測試不同數據量performance_test(100000);performance_test(500000);performance_test(1000000);performance_test(5000000);return 0;
}

最終優化建議：在實際工程中，建議創建動態閾值適配層，根據運行時數據特征自動選擇最優策略