簡單來說,?在回歸問題中,最常用的損失函數是均方誤差(MSE, Mean Squared Error)和平均絕對誤差(MAE, Mean Absolute Error)?。它們衡量的都是模型預測值(?)與真實值(y)之間的“距離”或“差異”。
下面我來詳細解釋它們的意思、區別和用途。
1. 均方誤差 (MSE) - L2 Loss?是什么意思???
均方誤差是回歸問題中最常見、最基礎的損失函數。它的計算方法是:
- 1.先計算每一個數據點的預測值與真實值的差(誤差)。
- 2.將這個差平方?(所以叫“均方”)。
- 3.將所有數據點的平方誤差加起來,再求平均。
?數學公式:??
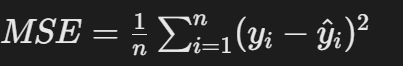
其中:
n是樣本數量。- yi?是第
i個樣本的真實值。 - y^?i?是模型對第
i個樣本的預測值。
?直觀理解與特點:??
- 放大大的誤差?:因為誤差被平方了,所以如果一個預測誤差很大(例如誤差為10,平方后變成100),它會比多個小誤差(例如多個誤差為1,平方后還是1)對總損失的貢獻大得多。
- ?曲線光滑?:數學性質很好,便于求導(它的導數是一個線性函數),這使得在梯度下降等優化算法中非常高效。
- 對異常值敏感?:這是它的一個主要缺點。如果數據中存在少數偏離很大的異常值,MSE會變得非常大,模型會為了擬合這些異常值而犧牲對整體數據的擬合效果。
?用途?:廣泛應用于各種回歸問題,是很多模型的默認損失函數。
2. 平均絕對誤差 (MAE) - L1 Loss?是什么意思???
平均絕對誤差的計算方法是:
- 1.計算每一個數據點的預測值與真實值的差的絕對值。
- 2.將所有絕對誤差加起來,再求平均。
?數學公式:??

?直觀理解與特點:??
- ?線性懲罰誤差?:無論誤差是1還是10,它對總損失的貢獻就是1和10,是線性的關系。不會特別放大大的誤差。
- ?對異常值更魯棒?:正因為它是線性懲罰,所以個別異常值不會像在MSE中那樣對損失產生巨大的影響,模型不會輕易被異常值“帶偏”。
- ?曲線不光滑?:在零點處不可導(導數突然從-1變為+1),這在優化時可能不如ME高效(但在實際中可以通過次梯度等方法解決)。
?用途?:當你認為數據中含有異常值,并且不希望模型過度關注這些異常點時,MAE是一個很好的選擇。
對比與總結
特性 | 均方誤差 (MSE) | 平均絕對誤差 (MAE) |
|---|---|---|
?計算方式? | 誤差的平方的平均 | 誤差的絕對值的平均 |
?對異常值? | ?敏感? | ?不敏感(更魯棒)?? |
?梯度性質? | 光滑,易于優化 | 在零點不可導,優化稍復雜 |
?解讀? | 懲罰大的誤差非常嚴厲 | 對所有誤差一視同仁 |
另一個重要的損失函數:Huber Loss
你可能會問,有沒有一個損失函數能結合MSE和MAE的優點呢?答案是有的,這就是 ?Huber Loss。
?Huber Loss? 是一個混合損失函數。它在一個閾值 δ(delta)范圍內,它的行為像MSE?(曲線光滑,易于優化);當誤差超過這個閾值時,它的行為像MAE?(對大的異常值更魯棒)。
?特點?:
- best of both worlds?:兼具MSE的優化友好和MAE的異常值魯棒性。
- 需要超參數?:你需要手動設置一個閾值 δ。
?用途?:當數據中明顯存在異常值,但你又不愿意完全使用MAE時,Huber Loss是一個非常出色的折中方案。
總結
- 分類問題的核心是預測概率分布,所以用交叉熵來衡量兩個分布之間的差異。
- ?回歸問題的核心是預測一個連續值,所以用基于距離的損失函數?(如MSE, MAE)來衡量預測值與真實值的差距。
- ?MSE是最常用的,數學性質好,但對異常值敏感。
- ?MAE對異常值不敏感,但優化起來稍麻煩。
- ?Huber Loss是一個聰明的結合體,在很多情況下能提供更好的性能。
選擇哪個損失函數取決于你的數據、模型和你最關心什么。通常可以從MSE開始,如果發現模型效果受異常值影響很大,再嘗試MAE或Huber Loss。
)


)




)



))





通信)
處理)