數據結構（C語言篇）：（六）單鏈表算法題（下）

前言

? ? ? ? 本篇博客將繼續介紹單鏈表相關的算法題，包括了鏈表的回文結構、相交鏈表、環形鏈表等。現在就讓我們正式開始吧！

一、鏈表的回文結構

????????題目鏈接：鏈表的回文結構_牛客題霸_牛客網

? ? ? ? 思路：創建數組（大小為900），遍歷鏈表將節點的值依次存儲在數組中，若數組為回文結構，則鏈表為回文結構。

? ? ? ? 解題核心邏輯如下：

將鏈表值復制到數組：遍歷鏈表，將所有節點的值存儲到數組中；
使用雙指針判斷回文：從數組兩端向中間遍歷，比較對應位置的值是否相等；
返回判斷結果：如果所有對應位置都相等，則是回文；否則不是。

? ? ? ? 完整代碼如下所示：

class PalindromeList {
public:bool chkPalindrome(ListNode* A) {// 創建固定大小的數組int arr[900] = {0};  // 假設鏈表長度不超過900// 遍歷鏈表，將值存儲到數組中ListNode* pcur = A;int i = 0;while(pcur) {arr[i++] = pcur->val;  // 存儲當前節點值，i后移pcur = pcur->next;     // 移動到下一個節點}// 使用雙指針判斷數組是否為回文int left = 0, right = i - 1;  // i是鏈表長度while(left < right) {if(arr[left] != arr[right]) {return false;  // 發現不對稱，不是回文}left++;right--;}return true;  // 所有對應位置都相等，是回文}
};

? ? ? ? 代碼的執行流程示例如下：假設鏈表為1 → 2 → 3 → 2 → 1 → NULL

步驟1：復制到數組
遍歷鏈表：arr[0]=1, arr[1]=2, arr[2]=3, arr[3]=2, arr[4]=1
i=5（鏈表長度）步驟2：雙指針判斷
left=0, right=4: 1==1 ?
left=1, right=3: 2==2 ?  
left=2, right=2: 循環結束
返回true

二、相交鏈表

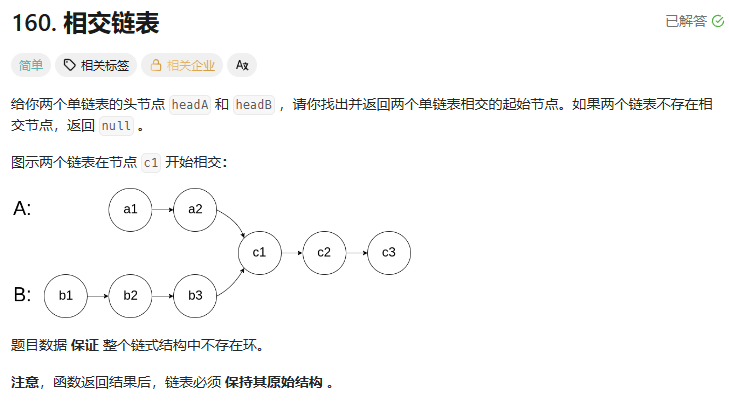
? ? ? ? 題目鏈接：160. 相交鏈表 - 力扣（LeetCode）

? ? ? ? 思路：求兩個鏈表的長度，長鏈表先走長度差步，短鏈表開始同步遍歷，找相同的結點。

? ? ? ? 解題核心邏輯如下：

計算鏈表長度：分別遍歷兩個鏈表，計算它們的長度；
計算長度差：求出兩個鏈表長度的差值；
對齊起點：讓較長的鏈表先移動長度差的步數；
同時遍歷：兩個指針同時移動，直到找到相同節點或到達末尾。

? ? ? ? 完整代碼如下：

typedef struct ListNode ListNode;struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {// 求鏈表的長度ListNode* pa = headA;ListNode* pb = headB;int sizeA = 0, sizeB = 0;// 計算鏈表A的長度while(pa) {++sizeA;pa = pa->next;}// 計算鏈表B的長度while(pb) {++sizeB;pb = pb->next;}// 求長度差int gap = abs(sizeA - sizeB);  // 求絕對值// 定義長短鏈表ListNode* shortList = headA;ListNode* longList = headB;// 確定哪個鏈表更長if(sizeA > sizeB) {longList = headA;shortList = headB;}// 長鏈表先走gap步，對齊起點while(gap--) {longList = longList->next;}// shortList和longList現在在同一起跑線while(shortList) {  // 或者用while(longList)if(shortList == longList) {  // 找到相交節點return shortList;}shortList = shortList->next;longList = longList->next;}// 鏈表不相交return NULL;
}

? ? ? ? 執行流程的示例如下：

????????假設：
????????鏈表A：1 → 2 → 3 → 4 → 5 → NULL（長度5）
????????鏈表B：9 → 8 → 4 → 5 → NULL（長度4，從節點4開始相交）

步驟1：計算長度
sizeA = 5, sizeB = 4步驟2：計算長度差
gap = |5-4| = 1步驟3：確定長短鏈表
longList = headA, shortList = headB步驟4：長鏈表先走1步
longList從節點1移動到節點2步驟5：同時遍歷
shortList=9, longList=2 → 不相等
shortList=8, longList=3 → 不相等  
shortList=4, longList=4 → 相等，返回節點4

三、環形鏈表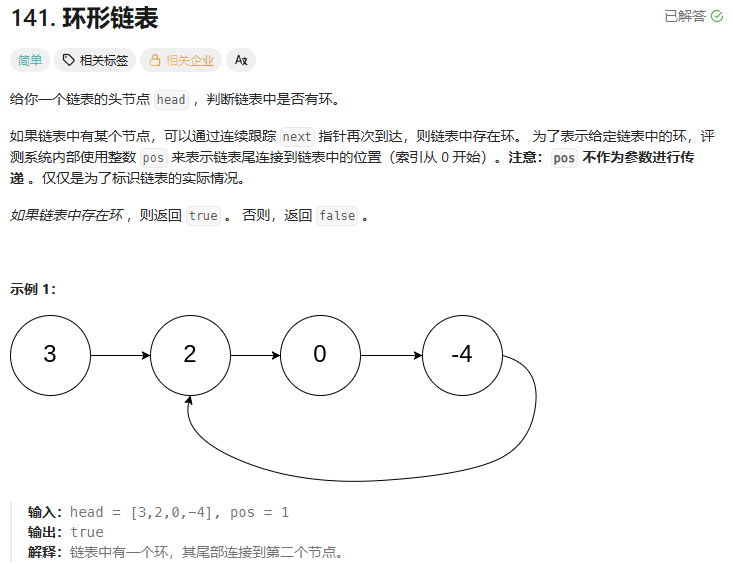

? ? ? ? 題目鏈接：141. 環形鏈表 - 力扣（LeetCode）

? ? ? ? 思路：采用快慢指針方法，慢指針每次走一步，快指針每次走兩步，如果slow和fast指向了同一個結點，說明鏈表帶環。

? ? ? ? 對于這個思路，我們可以嘗試證明一下：

? ? ? ? 證明1：在環形鏈表中，慢指針每次走一步，快指針每次走兩步，最終是否一定會相遇？

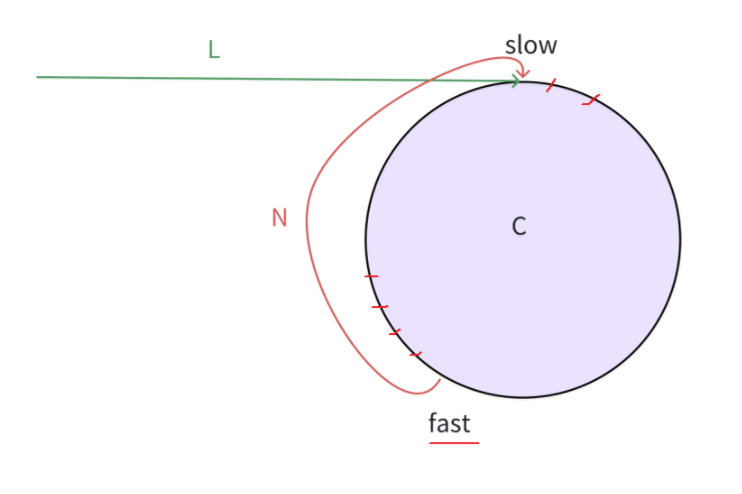
? ? ? ? 如上圖所示，假設此時slow剛入環，此時slow和fast之間的距離最大，為N。slow和fast各自移動一次之后，距離縮小2 - 1 = 1，則此時距離為N - 1，那么在移動N次之后，最后fast和slow之間的距離將縮短為0，兩指針相遇。

? ? ? ? 證明2：在環形鏈表中，慢指針每次走一步，快指針每次走3、4、5、……步，快慢指針在環形鏈表中還會相遇嗎？答案是一定會相遇。

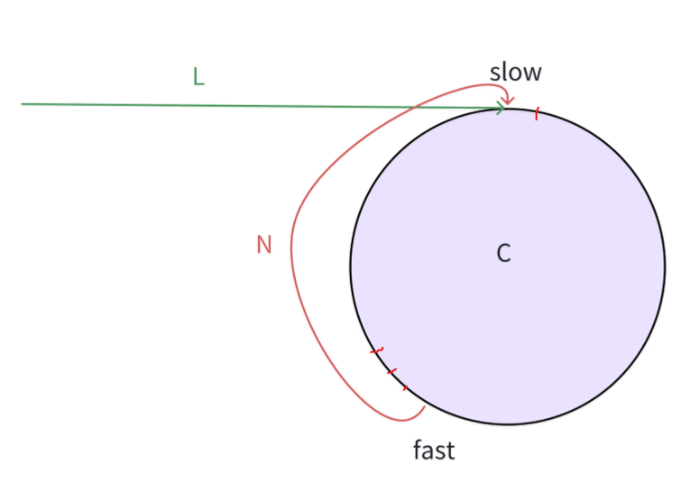
? ? ? ? 如上圖，假設此時slow剛入環，此時slow和fast之間的距離最大，為N。慢指針每次走一步，快指針每次走三步。每走一次，slow和fast之間距離就減小2，此時若N為偶數，那么最后兩者距離將減小為0，相遇；若N為奇數，那么距離會縮小為-1，此時就會套圈，兩者此時距離須以C-1來計算。若C-1為偶數，即C為奇數，那么一定會相遇；如果C-1為奇數，即C為偶數，則一定不會相遇。

? ? ? ? 下面我們再來推導一下快慢指針走的路程之間的關系：

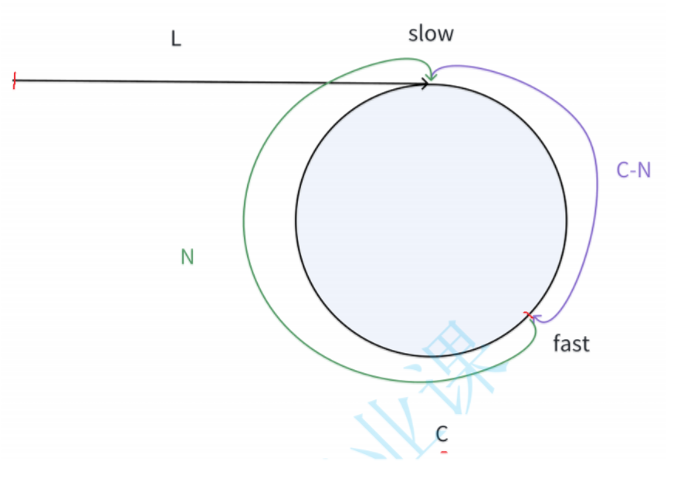
? ? ? ? 如上圖，我們假設慢指針每次走1步，快指針一次走3步，那么就有：3 * 慢指針 = 快指針。我們假設慢指針所走路程為L，則快指針所走路程為：L + C - N + nC。根據以上等式，就有：3L = L + C - N + nC，整理得到：2L = （n+1）C - N。如下：

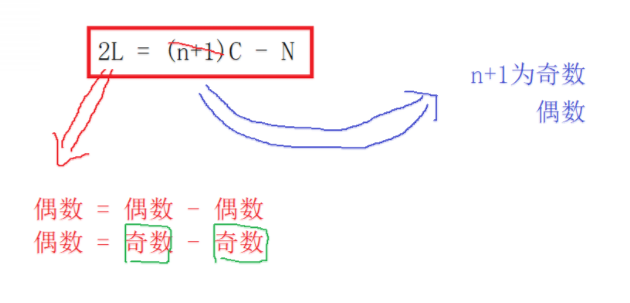
💡TIPS

????????雖然我們已經證明了快指針無論走多少步都可以滿足在帶環鏈表中相遇，但是在編寫代碼的時候會有額外的步驟引入，涉及到快慢指針的算法題中通常習慣使用慢指針走一步快指針走兩步的方式。

? ? ? ? 因此本題我們解題的核心邏輯如下：

???????1.? 初始化兩個指針：

????????slow（慢指針）：每次移動一步；

????????fast（快指針）：每次移動兩步。

? ? ? ? 2.? 同時移動指針：

????????????????慢指針每次移動1步，快指針每次移動2步；

????????????????如果鏈表有環，快慢指針最終會相遇；

????????????????如果鏈表無環，快指針會先到達NULL。

? ? ? ? 3.? 終止條件：

????????????????快慢指針相遇 → 有環，返回true；

????????????????快指針到達NULL → 無環，返回false。

????????完整代碼如下：

typedef struct ListNode ListNode;bool hasCycle(struct ListNode *head) {// 創建快慢指針ListNode* slow = head;  // 慢指針，每次移動1步ListNode* fast = head;  // 快指針，每次移動2步// 循環條件：快指針和快指針的下一個節點都不為NULLwhile(fast && fast->next) {slow = slow->next;        // 慢指針移動1步fast = fast->next->next;  // 快指針移動2步if(slow == fast) {        // 如果相遇return true;          // 鏈表有環}}// 快指針到達NULL，鏈表不帶環return false;
}

? ? ? ? 下面提供兩個執行流程的示例：

? ? ? ? 1.? 有環鏈表：1 → 2 → 3 → 4 → 5 → 3（形成環）

初始：slow=1, fast=1
第1輪：slow=2, fast=3
第2輪：slow=3, fast=5 ?
第3輪：slow=4, fast=3
第4輪：slow=5, fast=5 → 相遇，返回true初始：slow=1, fast=1
第1輪：slow=2, fast=3
第2輪：slow=3, fast=5 ?
第3輪：slow=4, fast=3
第4輪：slow=5, fast=5 → 相遇，返回true

? ? ? ? 2.? 無環鏈表： 1→ 2 → 3 → 4 → 5 → NULL

初始：slow=1, fast=1
第1輪：slow=2, fast=3
第2輪：slow=3, fast=5
第3輪：slow=4, fast=NULL → 循環結束，返回false

四、環形鏈表II

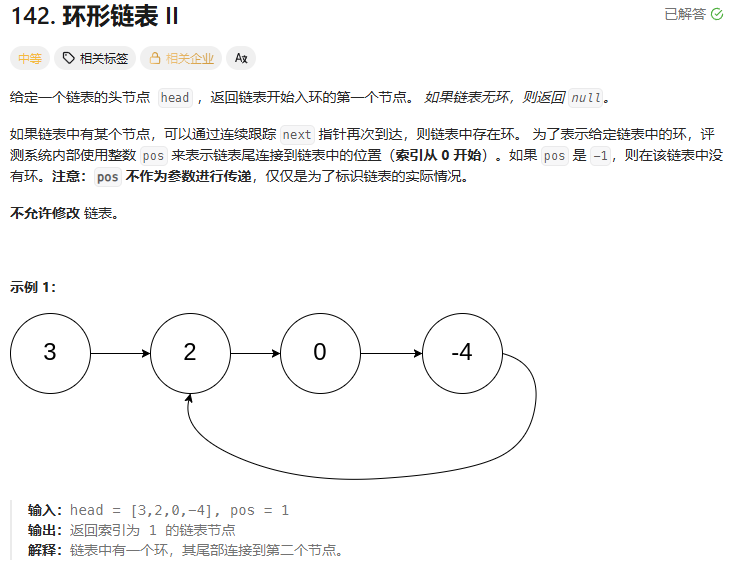
? ? ? ? 題目鏈接：142. 環形鏈表 II - 力扣（LeetCode）

? ? ? ? 思路：快慢指針，在環里一定會相遇。相遇點到入環結點的距離 == 頭結點到入環結點的距離

💡結論

? ? ? ? 讓一個指針從鏈表起始位置開始遍歷鏈表，同時讓一個指針從判環時相遇點的位置開始繞環運行，兩個指針都是每次均走一步，最終肯定會在入口點的位置相遇。

? ? ? ? 下面我們先來證明一下以上結論：

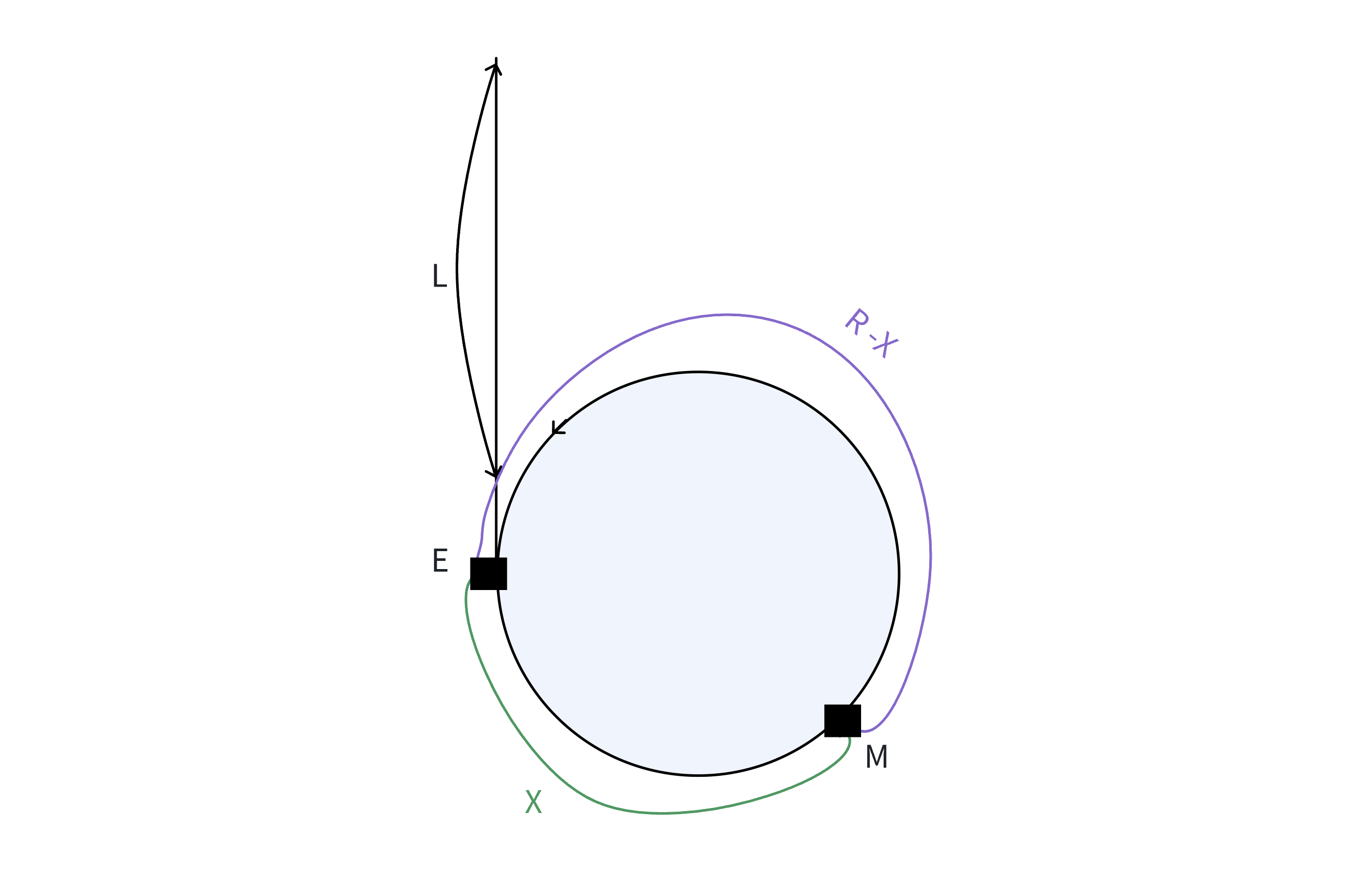
? ? ? ? H為鏈表的起始點，E為環的入口點，M與判環時候相遇點。

? ? ? ? 假設：環的長度為R，H到E的距離為L，E到M的距離為X，則：M到E的距離為R - X。

? ? ? ? 在判環的時候，快慢指針相遇時所走的路徑長度如下：

fast：L + X + nR
slow：L + X?

? ? ? ? 需要注意的是：

? ? ? ? 1.? 當慢指針進入環時，快指針可能已經在環中繞了n圈了，n至少為1。因為當快指針先進環走到M的位置，最后又會在M的位置與慢指針相遇。

? ? ? ? 2.? 慢指針進入環之后，快指針肯定會在慢指針走一圈之內追上慢指針。因為當慢指針進環之后，快慢指針之間的距離最多就是環的長度，而兩個指針在移動的時候，每次它們的距離都縮減一步，因此在慢指針移動一圈之前，快指針肯定是可以追上慢指針的，而快指針的速度是慢指針的兩倍，因此有如下關系：

? ? ? ? 2 * (L + X) = L + X + nR；

? ? ? ? L + X = nR；

? ? ? ? L = nR - X；

? ? ? ? L = (n - 1)R + (R - X)

? ? ? ? （n = 1、2、3、4、……、n，n的大小取決于環的大小，環越小n越大）

? ? ? ? 在極端情況下，我們假設n = 1，此時有：L = R - X。

? ? ? ? 即：一個指針從鏈表起始位置運行，一個指針從相遇點位置繞環，每次都走一步，兩個指針最終會在入口點的位置相遇。

? ? ? ? 完整代碼如下：

typedef struct ListNode ListNode;struct ListNode *detectCycle(struct ListNode *head) {// 創建快慢指針ListNode* slow = head;  // 慢指針，每次移動1步ListNode* fast = head;  // 快指針，每次移動2步// 第一階段：判斷是否有環while(fast && fast->next) {slow = slow->next;        // 慢指針移動1步fast = fast->next->next;  // 快指針移動2步if(slow == fast) {        // 如果相遇，說明有環// 第二階段：尋找環入口// 數學原理：頭節點到入口的距離 = 相遇點到入口的距離ListNode* pcur = head;while(pcur != slow) {pcur = pcur->next;  // pcur從頭節點開始slow = slow->next;  // slow從相遇點開始}return pcur;  // 相遇點即為環入口}}// 快指針到達NULL，鏈表不帶環return NULL;
}

? ? ? ? 執行流程示例如下：1 → 2 → 3 → 4 → 5 → 3（形成環，入口在節點3）

步驟1：判斷有環
slow=1, fast=1
slow=2, fast=3
slow=3, fast=5 ?
slow=4, fast=3
slow=5, fast=5 → 相遇在節點5

步驟2：尋找環入口
pcur=head=1, slow=5
pcur=2, slow=3
pcur=3, slow=3 → 相遇在節點3（環入口）
返回節點3