深度學習——03 神經網絡（2）-損失函數

2 損失函數

2.1 概述

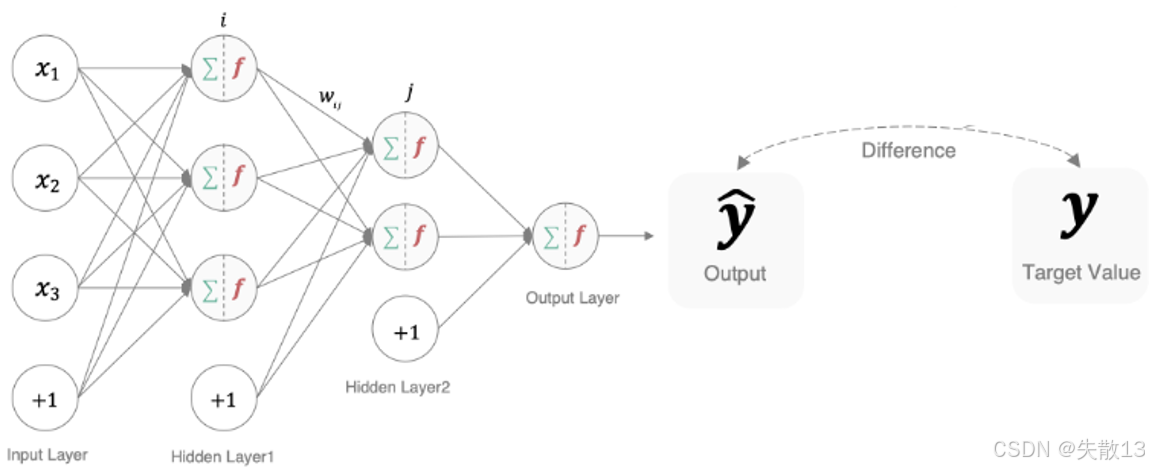
作用：衡量模型預測結果（ $y^\hat{y}$ ）和真實標簽（ $y$ ）的差異，差異越大，說明模型參數“質量越差”（需要調整）；
本質：深度學習訓練的“指揮棒”——反向傳播時，損失函數的梯度會告訴模型“怎么調整參數，才能讓預測更準”；
在不同文獻/框架中，損失函數可能有這些名字：

2.2 多分類任務損失函數

2.2.1 概述

在多分類任務通常使用 softmax 將 logits（神經網絡在經過最后一層線性變換后，尚未經過激活函數處理的原始輸出值）轉換為概率的形式，所以多分類的交叉熵損失也叫做 Softmax 損失
$\mathcal{L} = -\sum_{i=1}^{n} \mathbf{y}_i \log\left(S(f_\theta(\mathbf{x}_i))\right)$
- $yi\mathbf{y}_i$ ：真實標簽的 one-hot 編碼（比如二分類中，“貓”的標簽是 [1, 0] ，“狗”是 [0, 1]）；
- $fθ(xi)f_\theta(\mathbf{x}_i)$ ：模型對樣本 $xi\mathbf{x}_i$ 的“原始預測分數”（logits）；
- $S$ （Softmax 函數）：把 logits 轉換成“概率分布”（所有類別概率和為 1）；
- $L\mathcal{L}$ ：損失值，衡量“預測概率分布”和“真實標簽分布”的差異 → 差異越大，損失越大，模型越需要調整參數；
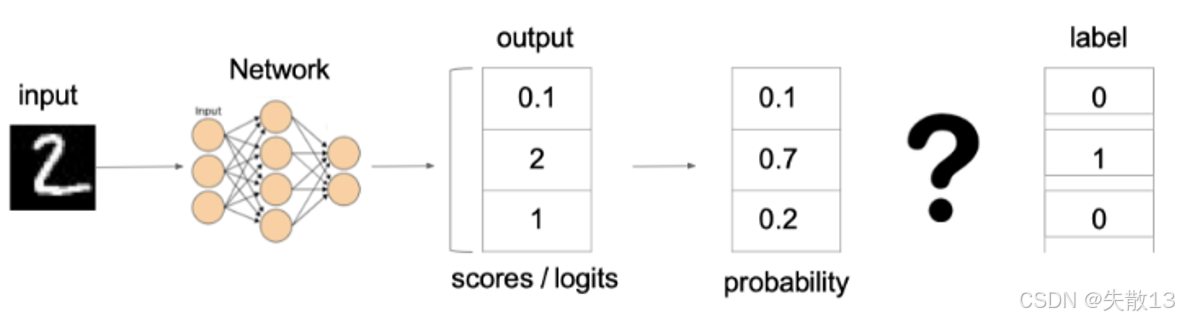
以“識別手寫數字 2”為例：
- 模型輸出：
  - logits（原始分數）：[0.1, 2, 1]（假設 3 分類，對應“0、1、2”）；
  - Softmax 轉換后概率：[0.1, 0.7, 0.2]（和為 1 ，模型認為“是 1 的概率 70%”）；
- 真實標簽：one-hot 編碼為 [0, 1, 0]；
- 損失計算：代入公式，只有真實類別（“1”）的 $yi\mathbf{y}_i$ 是 1，其他是 0 → 損失簡化為：
  $L=?(0log?(0.10)+1log?(0.7)+0log?(0.2))=?log?0.7\mathcal{L} = - \left( 0 \log(0.10) + 1 \log(0.7) + 0 \log(0.2) \right) = -\log 0.7$
  - 損失越小，說明預測概率越接近真實標簽 → 訓練時，模型會調整參數讓這個損失“盡可能小”；
多分類交叉熵損失的意義：
- 對齊概率分布：讓模型預測的“概率分布”盡可能貼近真實標簽的“one-hot 分布”（比如真實是“貓”，就希望“貓”的概率趨近 1，其他趨近 0）；
- 反向傳播的依據：損失值的梯度會告訴模型“怎么調整參數”，讓預測更準；

2.2.2 代碼

在 pytorch 中使用 nn.CrossEntropyLoss() 實現

import torch
import torch.nn as nn

# nn.CrossEntropyLoss()=softmax + 損失計算
# 說明：PyTorch中的CrossEntropyLoss會自動對輸入的預測值先做softmax，再計算交叉熵損失
def test1():# 設置真實值：可以是熱編碼后的結果也可以不進行熱編碼。這里演示的是“不進行獨熱編碼”的寫法，直接用類別索引表示真實標簽# 注意：真實標簽的類型必須是64位整型數據（torch.int64）# 解釋：y_true存儲的是樣本的真實類別索引，比如[1, 2]表示第1個樣本屬于類別1，第2個樣本屬于類別2y_true = torch.tensor([1, 2], dtype=torch.int64)# y_pred存儲模型的預測結果，形狀是[樣本數, 類別數]# 解釋：這里是2個樣本，3個類別，每個樣本輸出3個預測概率（已經是softmax后的結果也可以直接是logits，CrossEntropyLoss會自動處理）# 示例中：# 第1個樣本預測類別0概率0.2、類別1概率0.6、類別2概率0.2 # 第2個樣本預測類別0概率0.1、類別1概率0.8、類別2概率0.1 y_pred = torch.tensor([[0.2, 0.6, 0.2], [0.1, 0.8, 0.1]], dtype=torch.float32)# 實例化交叉熵損失# 解釋：創建CrossEntropyLoss對象，它會自動完成：# 1. 對y_pred做softmax（如果輸入的是logits）# 2. 與y_true（類別索引）計算交叉熵損失loss = nn.CrossEntropyLoss()# 計算損失結果# 解釋：將預測值y_pred和真實標簽y_true傳入loss函數，自動計算損失# .numpy()是為了把PyTorch的張量轉換成numpy數組，方便打印查看my_loss = loss(y_pred, y_true).numpy()# 打印損失值print('loss:', my_loss)

在這里插入圖片描述

2.2.3 輸出結果分析

輸入數據：
- 真實標簽 y_true = [1, 2]：表示 2 個樣本，第 1 個樣本屬于類別 1，第 2 個樣本屬于類別 2（類別索引從 0 開始）；
- 預測概率 y_pred = [[0.2, 0.6, 0.2], [0.1, 0.8, 0.1]]：
  - 第 1 個樣本對 3 個類別的預測概率：類別0：0.2、類別1：0.6、類別2：0.2；
  - 第 2 個樣本對 3 個類別的預測概率：類別0：0.1、類別1：0.8、類別2：0.1；
損失計算邏輯（CrossEntropyLoss）：CrossEntropyLoss 會自動對 y_pred 做 Softmax（如果輸入的是 logits），然后計算交叉熵。公式簡化為：
$\text{loss} = -\frac{1}{N} \sum_{i=1}^N \log\left( p_{\text{正確類別}} \right)$
- $ N $ 是樣本數量（這里 $ N=2 $ ）；
- $ p_{\text{正確類別}} $ 是樣本預測為“真實類別”的概率；
與2.2.1 概述中的公式本質是同一個損失邏輯，只是從 “簡化版（針對類別索引）” 和 “完整版（針對 one-hot 編碼）” 兩個角度描述多分類交叉熵損失，核心邏輯完全一致；
逐樣本計算
- 樣本 1（真實類別 1）：預測為類別 1 的概率是 0.6 → 損失項：$ -\log(0.6) \approx 0.5108 $；
- 樣本 2（真實類別 2）：預測為類別 2 的概率是 0.1 → 損失項：$ -\log(0.1) \approx 2.3026 $；
最終損失為兩個樣本的平均損失：
$\text{loss} = \frac{0.5108 + 2.3026}{2} \approx 1.4067$
但實際運行結果是 1.1200755，因為傳入的 y_pred 實際上已經是概率（softmax后的輸出），但CrossEntropyLoss再對它做softmax（logits -> softmax），這就導致計算不對，損失值偏小；
代碼輸出結果的含義：損失值 1.1200755 表示模型對這兩個樣本的預測“不夠準確”，需要反向傳播調整參數，讓正確類別的預測概率更高。

2.3 二分類任務損失函數

2.3.1 概述

在處理二分類任務時，我們不再使用 softmax 激活函數，而是使用 sigmoid 激活函數，那損失函數也相應地進行調整，使用二分類的交叉熵損失函數（也叫二元交叉熵，Binary Cross-Entropy, BCE ）：
$L=?ylog?y^?(1?y)log?(1?y^) L = -y \log \hat{y} - (1 - y) \log(1 - \hat{y})$
- 適用任務：二分類（比如“垃圾郵件/正常郵件”“患病/健康”）；
- 激活函數：搭配 sigmoid 激活函數，讓模型輸出 $ \hat{y} $ 是“樣本屬于正類的概率”（范圍 (0, 1)）；
- $ y $：樣本的真實標簽（二分類中，通常是 0 或 1 ，比如 1 代表“正類”，0 代表“負類”）；
- $ \hat{y} $：模型的預測概率（經過 sigmoid 后，是樣本屬于正類的概率）；
損失計算邏輯
- 如果樣本是正類（$ y=1 $ ）：公式簡化為 $ L = -\log \hat{y} $ → 預測概率 $ \hat{y} $ 越接近 1 ，損失越小；越接近 0 ，損失越大（懲罰模型“把正類預測成負類”）；
如果樣本是負類（$ y=0 $ ）：公式簡化為 $ L = -\log(1 - \hat{y}) $ → 預測概率 $ \hat{y} $ 越接近 0 ，損失越小；越接近 1 ，損失越大（懲罰模型“把負類預測成正類”）；
二元交叉熵的意義：
- 對齊概率：讓模型預測的“正類概率”盡可能貼近真實標簽（1 或 0 ）；
- 反向傳播依據：訓練時，損失的梯度會指導模型調整參數，讓預測更準確（比如預測正類概率不夠大，就調整參數讓它變大）。

2.3.2 代碼

在 pytorch 中使用nn.BCELoss()實現

def test2():# 設置真實值和預測值# 預測值是sigmoid輸出的結果（已經過sigmoid歸一化到0~1區間）# 解釋：y_pred存儲3個樣本的預測概率，requires_grad=True表示需要計算梯度（用于反向傳播）y_pred = torch.tensor([0.6901, 0.5459, 0.2469], requires_grad=True)# 真實標簽：0表示負類，1表示正類，dtype=torch.float32是BCELoss的輸入要求# 解釋：y_true和y_pred長度必須一致，每個元素對應一個樣本的真實類別（0/1）y_true = torch.tensor([0, 1, 0], dtype=torch.float32)# 實例化二分類交叉熵損失（BCE損失）# 解釋：nn.BCELoss專門用于二分類任務，計算預測概率與真實標簽的交叉熵criterion = nn.BCELoss()# 計算損失# 解釋：將預測概率y_pred和真實標簽y_true傳入損失函數# .detach()是為了阻斷反向傳播（避免計算圖占用內存），.numpy()轉成numpy數組方便打印my_loss = criterion(y_pred, y_true).detach().numpy()# 打印最終損失值print('loss: ', my_loss)test2()

在這里插入圖片描述

2.3.3 輸出結果分析

輸入數據
- 預測概率 y_pred = [0.6901, 0.5459, 0.2469]：3 個樣本的預測概率（已經過 Sigmoid 歸一化到 0~1）；
- 真實標簽 y_true = [0, 1, 0]：3 個樣本的真實類別，0 表示負類，1 表示正類；
損失計算邏輯（BCELoss）：BCELoss 用于二分類，公式為
$loss=?1N∑i=1N(yilog?(y^i)+(1?yi)log?(1?y^i)) \text{loss} = -\frac{1}{N} \sum_{i=1}^N \left( y_i \log(\hat{y}_i) + (1-y_i) \log(1-\hat{y}_i) \right)$
- $ y_i $ 是真實標簽（0 或 1）
- $ \hat{y}_i $ 是預測概率
逐樣本計算
- 樣本 1（真實標簽 0）：損失項：$ -(0 \cdot \log(0.6901) + 1 \cdot \log(1-0.6901)) = -\log(0.3099) \approx 1.173 $；
- 樣本 2（真實標簽 1）：損失項：$ -(1 \cdot \log(0.5459) + 0 \cdot \log(1-0.5459)) = -\log(0.5459) \approx 0.604 $；
- 樣本 3（真實標簽 0）：損失項：$ -(0 \cdot \log(0.2469) + 1 \cdot \log(1-0.2469)) = -\log(0.7531) \approx 0.283 $；
最終損失為平均 3 個樣本的損失：
$\text{loss} = \frac{1.173 + 0.604 + 0.283}{3} \approx 0.6867$
代碼輸出結果的含義：損失值 0.6867941 表示模型對這 3 個樣本的預測“不夠準確”，需要反向傳播調整參數，讓正類樣本的預測概率更高，負類樣本的預測概率更低。

2.4 回歸任務損失函數-MAE損失函數

2.4.1 概述

MAE（Mean Absolute Error，平均絕對誤差）損失函數，也叫 L1 Loss，，是以絕對誤差作為距離。公式：
$\mathcal{L} = \frac{1}{n} \sum_{i=1}^{n} \left| y_i - f_\theta(x_i) \right|$
- $ y_i $：樣本的真實值；
- $ f_\theta(x_i) $：模型對樣本 $ x_i $ 的預測值；
- $ n $：樣本數量；
- $ \mathcal{L} $：損失值，衡量“預測值與真實值的絕對誤差的平均值” → 誤差越大，損失越大，模型越需要調整參數；
特點：
- 稀疏性（正則化效果）：MAE 對“大誤差”更敏感（因為是絕對值，大誤差不會被“平方縮小”），會懲罰模型預測偏差大的情況。因此常被用作“正則項”，約束模型參數，避免過擬合；
- 梯度不光滑問題：在預測值 = 真實值（誤差為 0）時，絕對值函數的梯度不連續（左右導數突變）。訓練時，梯度下降可能“跳過極小值點”，導致模型收斂到次優解；
圖像：
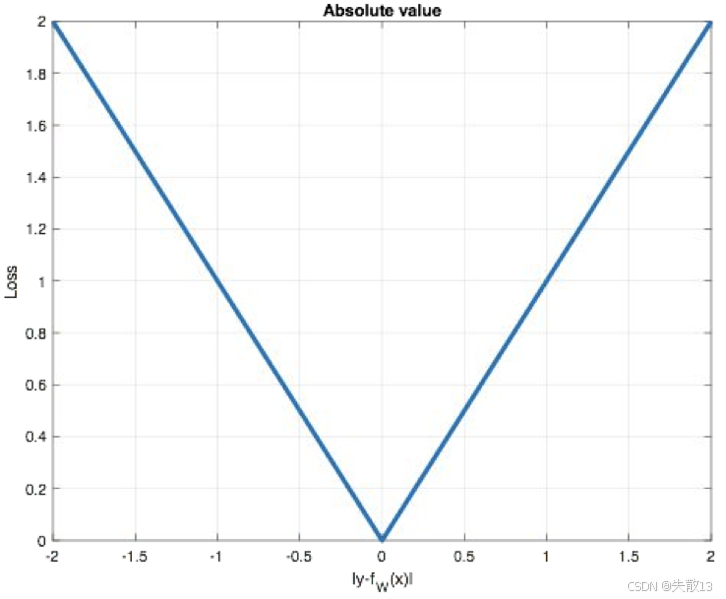
- 橫軸：預測誤差（$ |y_i - f_\theta(x_i)| $ ）；縱軸：損失值（$ \mathcal{L} $ ）；
- 圖像是“V 型”，體現 MAE 的特點：
  - 誤差越大，損失線性增長（懲罰大誤差）；
  - 誤差為 0 時，損失最小（模型預測完全準確）。

2.4.2 代碼

在 pytorch 中使用 nn.L1Loss() 實現：

# 定義測試函數，演示 MAE（L1 Loss）的計算流程
def test3():# 設置預測值和真實值# y_pred：模型的預測結果，需要計算梯度（requires_grad=True）用于反向傳播# 這里是 3 個樣本的預測值：[1.0, 1.0, 1.9]y_pred = torch.tensor([1.0, 1.0, 1.9], requires_grad=True)# y_true：樣本的真實標簽，dtype=torch.float32 是 L1Loss 的輸入要求# 這里是 3 個樣本的真實值：[2.0, 2.0, 2.0]y_true = torch.tensor([2.0, 2.0, 2.0], dtype=torch.float32)# 實例化 MAE 損失函數（L1 Loss）# nn.L1Loss 會計算預測值與真實值的絕對誤差的平均值criterion = nn.L1Loss()# 計算損失# 將預測值 y_pred 和真實值 y_true 傳入損失函數，自動計算 MAE# .detach() 用于切斷反向傳播（避免保留計算圖占用內存）# .numpy() 轉成 numpy 數組，方便打印查看結果my_loss = criterion(y_pred, y_true).detach().numpy()# 打印最終損失值print('loss:', my_loss)
test3()

在這里插入圖片描述

2.4.3 輸出結果分析

MAE 損失函數的計算公式為：
$\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} \left| y_{\text{pred},i} - y_{\text{true},i} \right|$
- 其中：
  - $ n $ 是樣本數量（這里 $ n = 3 $ ，對應 3 個預測值和 3 個真實值）；
  - $ y_{\text{pred},i} $ 是模型對第 $ i $ 個樣本的預測值；
  - $ y_{\text{true},i} $ 是第 $ i $ 個樣本的真實標簽值；
代碼中給出的預測值和真實值分別是：
- 預測值 $ y_{\text{pred}} = [1.0, 1.0, 1.9] $
- 真實值 $ y_{\text{true}} = [2.0, 2.0, 2.0] $
逐樣本計算絕對誤差，再求平均：
1. 第 1 個樣本絕對誤差：$ |1.0 - 2.0| = 1.0 $
2. 第 2 個樣本絕對誤差：$ |1.0 - 2.0| = 1.0 $
3. 第 3 個樣本絕對誤差：$ |1.9 - 2.0| = 0.1 $
將這些絕對誤差求平均：
$\text{MAE} = \frac{1.0 + 1.0 + 0.1}{3} = \frac{2.1}{3} = 0.7$
代碼輸出結果的含義：
- 最終輸出 loss: 0.7 ，表示模型預測值與真實值的平均絕對誤差是 0.7；
- 損失值越小，說明模型預測越接近真實標簽；損失值越大，說明預測偏差越大，需要繼續調整模型參數（如通過反向傳播優化網絡權重）來減小誤差。

2.5 回歸任務損失函數-MSE損失函數

2.5.1 概述

MSE（均方誤差，Mean Squared Error）損失函數，也叫 L2 Loss 或歐氏距離，它以誤差的平方和的均值作為距離。公式：
$\mathcal{L} = \frac{1}{n} \sum_{i=1}^{n} \left( y_i - f_\theta(x_i) \right)^2$
- $ y_i $：樣本的真實值（比如實際房價）；
- $ f_\theta(x_i) $：模型對樣本 $ x_i $ 的預測值（比如模型預測的房價）；
- $ n $：樣本數量；
- $ \mathcal{L} $：損失值，衡量“預測值與真實值的平方誤差的平均值” → 誤差越大，損失越大，模型越需要調整參數；
特點：
- 作為正則項（L2 正則）：MSE 的“平方”特性，會放大模型的“大誤差”（比如預測偏差 2 → 平方后是 4 ，偏差 3 → 平方后是 9）。這種“懲罰大誤差”的特點，讓 MSE 常被用作正則項（比如 L2 正則），約束模型參數不要過大，避免過擬合；
- 梯度爆炸風險：當預測值與真實值偏差很大時（比如模型預測房價 100 萬，實際是 1000 萬），平方誤差會非常大（$ (1000-100)^2 = 810000 $）。反向傳播時，梯度（損失對參數的導數）也會被“平方放大”，可能導致梯度爆炸（梯度值瞬間變得極大，模型參數更新幅度過大，無法穩定訓練）；
圖像：
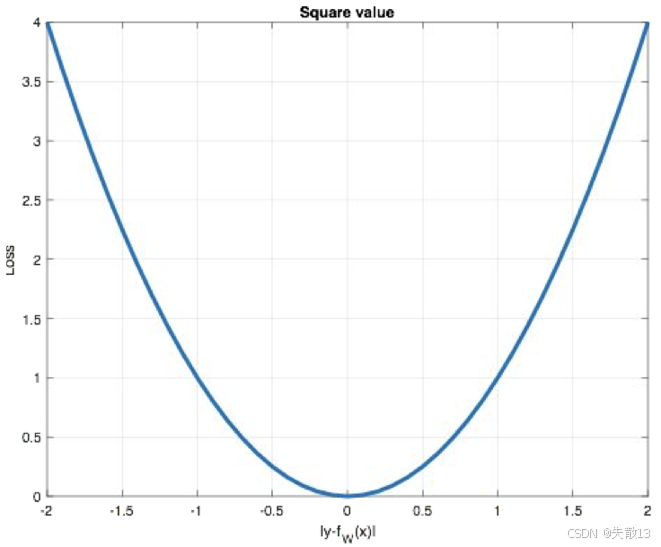
- 橫軸：預測誤差（$ y_i - f_\theta(x_i) $ ），縱軸：損失值（$ \mathcal{L} $ ）；
- 曲線是“U 型”，體現 MSE 的特點：
  - 誤差越大，損失指數級增長（平方放大誤差）；
  - 誤差為 0 時，損失最小（模型預測完全準確）；
適合場景：數據分布較均勻、無極端異常值，且希望模型對“小誤差更敏感”的回歸任務（比如預測溫度，誤差 1℃ 影響大，需要重點優化）；
對比 MAE（L1 Loss）：
- MAE 對異常值魯棒（絕對值不放大誤差），但梯度在 0 點不連續（訓練可能不穩定）；
- MSE 對異常值更敏感（平方放大誤差），但梯度光滑（訓練更穩定）。

2.5.2 代碼

在 pytorch 中使用 nn.MSELoss() 實現

def test4():# 準備預測值和真實值# y_pred: 模型輸出的預測結果，需要計算梯度(requires_grad=True)用于反向傳播更新參數# 這里模擬 3 個樣本的預測值: [1.0, 1.0, 1.9]y_pred = torch.tensor([1.0, 1.0, 1.9], requires_grad=True)# y_true: 樣本的真實標簽，dtype=torch.float32 是 MSELoss 要求的輸入類型# 這里模擬 3 個樣本的真實值: [2.0, 2.0, 2.0]y_true = torch.tensor([2.0, 2.0, 2.0], dtype=torch.float32)# 初始化 MSE 損失函數# nn.MSELoss 會計算預測值與真實值的均方誤差（平方誤差的平均值）loss_function = nn.MSELoss()# 計算損失值# 將預測值和真實值傳入損失函數，自動執行: # 1) 逐樣本計算 (y_pred - y_true)^2 # 2) 對所有樣本的平方誤差求平均# .detach() 用于切斷反向傳播鏈路（避免保存計算圖占用內存）# .numpy() 轉換為 numpy 數組方便打印查看calculated_loss = loss_function(y_pred, y_true).detach().numpy()# 打印最終損失結果print('loss:', calculated_loss)
test4()

在這里插入圖片描述

2.5.3 輸出結果分析

MSE 損失函數的公式：
$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} \left( y_{\text{pred},i} - y_{\text{true},i} \right)^2$
- $ n $：樣本數量（這里 $ n = 3 $ ，3 個樣本）；
- $ y_{\text{pred},i} $：模型對第 $ i $ 個樣本的預測值；
- $ y_{\text{true},i} $：第 $ i $ 個樣本的真實值；
代碼中，預測值和真實值分別為：
- 預測值 $ y_{\text{pred}} = [1.0, 1.0, 1.9] $
- 真實值 $ y_{\text{true}} = [2.0, 2.0, 2.0] $
對每個樣本，計算“預測值 - 真實值”的平方：
- 樣本 1：$ (1.0 - 2.0)^2 = (-1.0)^2 = 1.0 $
- 樣本 2：$ (1.0 - 2.0)^2 = (-1.0)^2 = 1.0 $
- 樣本 3：$ (1.9 - 2.0)^2 = (-0.1)^2 = 0.01 $
計算“平均平方誤差”：將所有樣本的平方誤差求和，再除以樣本數量 $ n = 3 $：
$\text{MSE} = \frac{1.0 + 1.0 + 0.01}{3} = \frac{2.01}{3} = 0.67$
代碼輸出結果的含義：
- 輸出 loss: 0.67 表示模型預測值與真實值的均方誤差是 0.67；
- 損失值越小，說明模型預測越接近真實標簽；損失值越大，說明預測偏差越大，需要繼續調整模型參數（如通過反向傳播優化網絡權重）來減小誤差；
MSE 的特點（結合代碼場景）
- 放大“大誤差”：MSE 對“大誤差”更敏感（平方會放大誤差）。如果模型預測偏差大（比如樣本 1、2 的偏差是 1.0），平方后會讓損失更顯著，推動模型優先優化這些“大誤差”；
- 梯度更新特性：MSE 的梯度（損失對模型參數的導數）與“預測誤差”成正比（梯度 = $ 2 \times (y_{\text{pred}} - y_{\text{true}}) $）。誤差越大，梯度越大，模型參數更新幅度也越大，這可能導致“梯度爆炸”（但本示例誤差小，無此問題）。

2.6 回歸任務損失函數-smooth L1損失函數

2.6.1 概述

Smooth L1 是分段函數，定義：
$\text{smooth}_{L_1}(x) = \begin{cases} 0.5x^2 & \text{如果 } |x| < 1 \\ |x| - 0.5 & \text{否則} \end{cases}$
- $x$ ：預測值與真實值的誤差（$ x = f(x) - y $ ，即模型預測偏差）；
設計目的（解決 L1/L2 的缺點）
損失函數缺點 Smooth L1 的改進邏輯
L1（MAE）誤差為 0 時梯度不連續（影響訓練穩定性）當 $
L2（MSE）誤差大時梯度爆炸（異常值敏感）當 $
圖像：
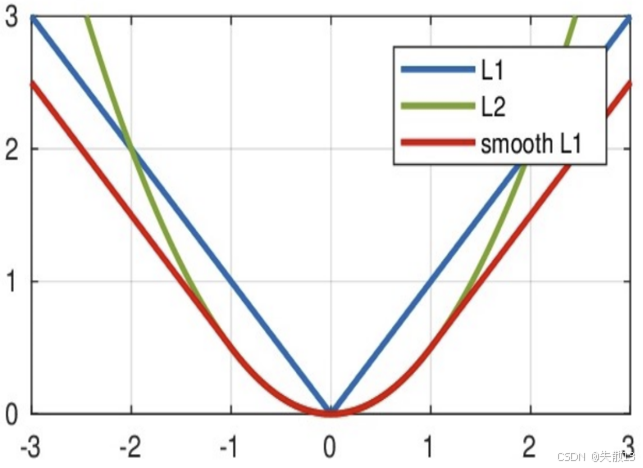
- L1（藍色）：V 型，誤差大時梯度穩定，但 0 點不光滑；
- L2（綠色）：U 型，誤差小時梯度光滑，但誤差大時梯度爆炸；
- Smooth L1（紅色）：
  - 誤差小（$ |x| < 1 $ ）：曲線和 L2 重合（梯度光滑）；
  - 誤差大（$ |x| \geq 1 $ ）：曲線和 L1 重合（梯度穩定，避免爆炸）；
Smooth L1 結合了 L1 和 L2 的優點，適合：回歸任務中存在異常值（需要 L1 的魯棒性），但希望訓練更穩定（需要 L2 的光滑梯度）的場景（比如目標檢測中的邊界框回歸）。

損失函數	缺點	Smooth L1 的改進邏輯
L1（MAE）	誤差為 0 時梯度不連續（影響訓練穩定性）	當 $
L2（MSE）	誤差大時梯度爆炸（異常值敏感）	當 $

2.6.2 代碼

在 pytorch 中使用nn.SmoothL1Loss()實現：

def test5():# 準備預測值和真實值# y_true: 樣本的真實標簽，這里是 [0, 3]（2個樣本的真實值）y_true = torch.tensor([0, 3])# y_pred: 模型的預測結果，需要計算梯度(requires_grad=True)用于反向傳播# 這里是 2 個樣本的預測值: [0.6, 0.4]y_pred = torch.tensor([0.6, 0.4], requires_grad=True)# 初始化 Smooth L1 損失函數# nn.SmoothL1Loss 會根據預測誤差的大小，自動切換 L1/L2 損失邏輯：# - 誤差小（|x| < 1）: 用 L2 損失 (0.5x2)# - 誤差大（|x| ≥ 1）: 用 L1 損失 (|x| - 0.5)criterion = nn.SmoothL1Loss()# 3. 計算損失值# 逐樣本計算誤差 x = y_pred - y_true，再代入 Smooth L1 公式# .detach() 切斷反向傳播（避免保存計算圖占用內存）# .numpy() 轉成 numpy 數組方便打印calculated_loss = criterion(y_pred, y_true).detach().numpy()# 打印最終損失print('loss:', calculated_loss)
test5()

在這里插入圖片描述

2.6.3 輸出結果分析

Smooth L1 是分段函數，公式：
$\text{smooth}_{L_1}(x) = \begin{cases} 0.5x^2 & \text{如果 } |x| < 1 \text{（誤差小，用 L2 損失）} \\ |x| - 0.5 & \text{如果 } |x| \geq 1 \text{（誤差大，用 L1 損失）} \end{cases}$
- 其中，$ x = y_{\text{pred}} - y_{\text{true}} $（預測值與真實值的誤差）；
代碼中，預測值和真實值分別為：
- 預測值 $ y_{\text{pred}} = [0.6, 0.4] $
- 真實值 $ y_{\text{true}} = [0, 3] $
對每個樣本，計算 $ x = y_{\text{pred}} - y_{\text{true}} $：
- 樣本 1：$ x_1 = 0.6 - 0 = 0.6 $
- 樣本 2：$ x_2 = 0.4 - 3 = -2.6 $
分段計算“樣本損失”，根據 Smooth L1 的分段邏輯：
- 樣本 1（$ |x_1| = 0.6 < 1 $，誤差小 → 用 L2 損失）
  $\text{損失}_1 = 0.5 \times (0.6)^2 = 0.5 \times 0.36 = 0.18$
- 樣本 2（$ |x_2| = 2.6 \geq 1 $，誤差大 → 用 L1 損失）
  $\text{損失}_2 = |-2.6| - 0.5 = 2.6 - 0.5 = 2.1$
Smooth L1 損失默認返回所有樣本損失的平均值：

$\text{總損失} = \frac{\text{損失}_1 + \text{損失}_2}{2} = \frac{0.18 + 2.1}{2} = \frac{2.28}{2} = 1.14$
代碼輸出結果的含義：
- 輸出 loss: 1.14 表示：模型預測值與真實值的Smooth L1 損失是 1.14；
- 損失值綜合了“誤差小樣本的 L2 平滑”和“誤差大樣本的 L1 魯棒性”，既避免了 L2 對異常值的敏感，又解決了 L1 在誤差為 0 時的梯度不連續問題，讓模型訓練更穩定。