目錄

簡介

一、dbscan相關概念

二、dbscan的API

三、案例分析

1. 導入所需庫

2. 數據讀取與預處理

3. 數據準備

4. DBSCAN 參數調優

5. 確定最佳參數并應用

總結

---

簡介

????????本次我們將聚焦于一款極具特色的聚類算法 ——DBSCAN。相較于 K-means 等需要預先指定簇數量的算法，DBSCAN 以其 “無監督自適應” 的特性，在聚類領域占據著不可替代的地位。

????????在這一課中，我們會深入剖析 DBSCAN 算法的核心原理。你將了解到它如何通過 “密度可達” 和 “核心對象” 等關鍵概念，自動發現數據集中任意形狀的簇，還能識別出那些不屬于任何簇的噪聲點。這一特性讓它在處理非凸形狀、存在噪聲的數據時，展現出遠超傳統聚類算法的優勢。

一、dbscan相關概念

概念：
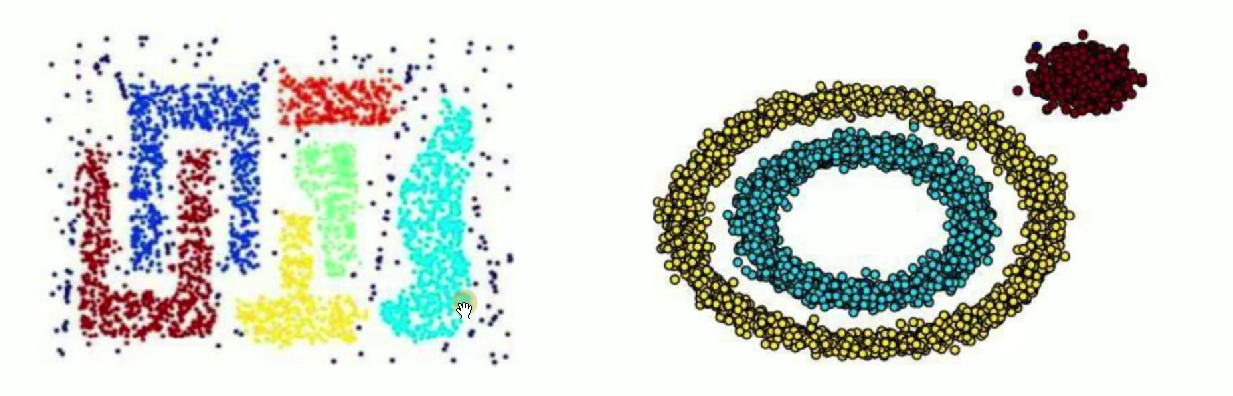
????????基于密度的帶噪聲的空間聚類應用算法，它是將簇定義為密度相連的點的最大集合，能夠把具有足夠高密度的區域劃分為簇，并在噪聲的空間數據集中發現任意形狀的聚類。

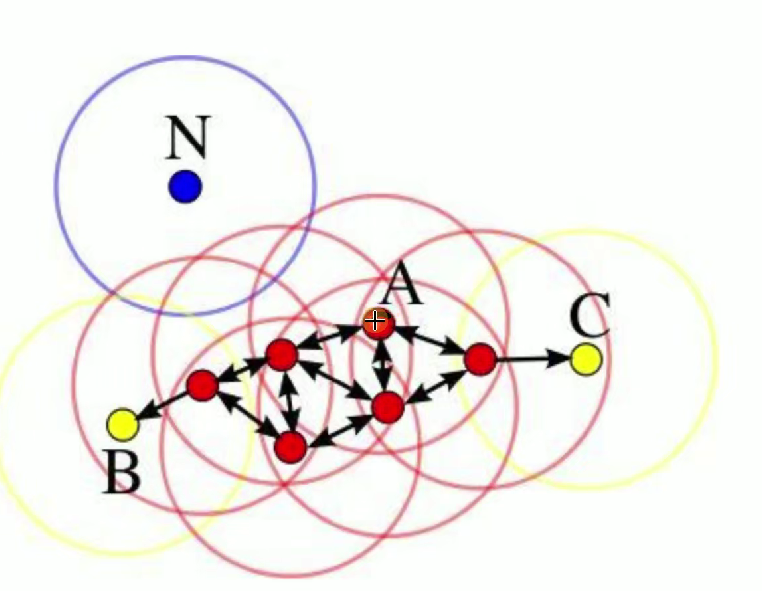
1. 核心對象：A 點在 DBSCAN 算法中，如果一個點的 E 鄰域內包含的點的數量大于等于某個給定的閾值（MinPts） ，則這個點被稱為核心對象。圖中的 A 點就是核心對象，以 A 為圓心的紅色圓圈代表其 E 鄰域，可以看到在這個鄰域內有足夠多的其他點（超過了算法設定的閾值）。
2. E 鄰域：給定對象半徑為 E 內的區域，對于給定的一個對象（點），以該對象為中心，半徑為 E 的區域就是這個對象的 E 鄰域。圖中圍繞每個點的圓圈就代表了相應點的 E 鄰域，例如紅色圓圈是核心對象 A 的 E 鄰域，藍色圓圈是點 N 的 E 鄰域 ，黃色圓圈是點 B 和點 C 的 E 鄰域。
3. 直接密度可達：如果點 p 在點 q 的 E 鄰域內，并且 q 是核心對象，那么我們稱點 p 從點 q 直接密度可達。在圖中，一些紅色的點位于核心對象 A 的 E 鄰域內，這些點就從 A 點直接密度可達。
4. 密度可達：如果存在一個點鏈 p1, p2, ..., pn，其中 p1 = q，pn = p，對于 pi ∈ {p1, p2, ..., pn-1}，pi+1 從 pi 直接密度可達，那么我們稱點 p 從點 q 密度可達。例如圖中，點 B 和點 C 雖然不在核心對象 A 的 E 鄰域內，但可以通過一系列直接密度可達的點（圖中的紅色點鏈 ），從 A 點密度可達。
5. 邊界點：B 點、C 點邊界點是指在其 E 鄰域內有點屬于某個簇，但自身不是核心對象的點。圖中的 B 點和 C 點就是邊界點，它們的 E 鄰域（黃色圓圈 ）內有來自核心對象 A 所在簇的點，但它們自身的 E 鄰域內點數未達到成為核心對象的閾值。
6. 離群點：N 點??離群點是指既不是核心對象也不是邊界點的點，也就是不在任何簇中的點。

實現過程：

1. 輸入數據集
2. 指定半徑；
3. 指定密度閾值；

二、dbscan的API

class sklearn.cluster.DBSCAN(eps=0.5, min_samples=5, 
metric='euclidean', metric_params=None, algorithm='auto', leaf_size=30, p=None, n_jobs=None)

參數解釋

• eps：即圖中提到的 “半徑” ，DBSCAN 算法中定義的鄰域半徑。它決定了一個點的鄰域范圍，在這個范圍內去判斷點的密度情況，默認值?0.5。
• min_samples：可以理解為密度閾值相關，即構成核心點所需的鄰域（eps?范圍內）最少樣本數量，用于判斷核心對象，默認?5?。
• metric：用于計算距離的度量方式，這里是?euclidean（歐幾里得距離），也可選擇其他距離度量，比如曼哈頓距離等，默認用歐氏距離衡量點與點之間的遠近。
• metric_params：度量函數的額外參數，一般用默認值?None?即可，當?metric?有特殊參數需求時才設置。
• algorithm：近鄰搜索算法，auto?表示讓算法自動選擇合適的近鄰搜索方法（如?ball_tree、kd_tree?或?brute?等 ），根據數據情況自適應選擇。
• leaf_size：構建?BallTree?或?KDTree?時的葉子節點大小，會影響樹構建和查詢的效率，默認?30?。
• p：當?metric?為閔可夫斯基距離（minkowski）時，p?是閔可夫斯基距離的階數，p=2?就是歐氏距離，p=1?是曼哈頓距離；若?metric?不是閔可夫斯基距離，該參數無意義，默認?None?。
• n_jobs：用于并行計算的 CPU 核心數，None?表示使用 1 個核心，-1?表示使用所有可用核心，可加速近鄰搜索等過程。

三、案例分析

1. 導入所需庫

import pandas as pd
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import adjusted_rand_score, normalized_mutual_info_score
import numpy as np

2. 數據讀取與預處理

# 讀取訓練集和測試集數據
data_train = pd.read_csv("datingTestSet2.txt", sep='\t', encoding='utf-8', engine='python', header=None)
data_test = pd.read_csv("datingTestSet1.txt", sep='\t', encoding='utf-8', engine='python', header=None)# 初始化標準化器
scaler = StandardScaler()# 對特征列進行標準化（所有列除了最后一列，假設最后一列是標簽）
data_train.iloc[:, :-1] = scaler.fit_transform(data_train.iloc[:, :-1])
data_test.iloc[:, :-1] = scaler.transform(data_test.iloc[:, :-1])

• 標準化處理是 DBSCAN 等基于距離的算法必需的步驟，因為它對特征的尺度敏感
• 測試集使用訓練集的標準化參數，避免數據泄露

3. 數據準備

x_train = data_train.iloc[:, :-1]  # 訓練集特征
x_test = data_test.iloc[:, :-1]    # 測試集特征
y_train_true = data_train.iloc[:, -1]  # 訓練集真實標簽
y_test_true = data_test.iloc[:, -1]    # 測試集真實標簽

4. DBSCAN 參數調優

# 定義要測試的eps參數范圍
scores = []
eps_param_range = [0.09, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6]for eps in eps_param_range:# 初始化并訓練DBSCAN模型dbscan = DBSCAN(eps=eps, min_samples=2)train_labels = dbscan.fit_predict(x_train)# 計算評估指標，忽略噪聲點(-1)mask = train_labels != -1if np.sum(mask) > 0:  # 確保有非噪聲點ari = adjusted_rand_score(y_train_true[mask], train_labels[mask])nmi = normalized_mutual_info_score(y_train_true[mask], train_labels[mask])score_mean = (ari + nmi) / 2  # 平均得分scores.append(score_mean)print(f"eps等于{eps}的平均得分(ARI+NMI)/2為{score_mean:.4f}")else:print(f"eps等于{eps}時，所有樣本都被標記為噪聲點")scores.append(-1)

• eps是 DBSCAN 中最重要的參數，定義了鄰域半徑
• min_samples是構成核心點所需的最小樣本數
• 使用 ARI（調整蘭德指數）和 NMI（標準化互信息）作為評估指標，這兩個指標都需要真實標簽
• 忽略噪聲點（標簽為 - 1）對評估的影響

5. 確定最佳參數并應用

# 找到最佳的eps參數
best_eps = eps_param_range[np.argmax(scores)]
print(f"最好的eps是：{best_eps}")# 使用最佳參數重新訓練模型
best_dbscan = DBSCAN(eps=best_eps, min_samples=2)
train_labels = best_dbscan.fit_predict(x_train)
print("訓練集聚類標簽:\n", train_labels)# 對測試集進行預測
test_labels = best_dbscan.fit_predict(x_test)
print("測試集聚類標簽:\n", test_labels)

• 選擇平均得分最高的eps作為最佳參數
• 使用最佳參數重新訓練模型并輸出聚類結果
• 對測試集進行聚類并輸出結果

總結

????????這個案例我做的比較簡單，重點是學習其代碼的邏輯、這個代碼框架可以作為 DBSCAN 算法應用的模板，只需根據實際數據集調整文件路徑和參數范圍即可。