摘要
通過增加測試時計算量使大型語言模型(LLMs)提升輸出效果,是構建能基于開放自然語言自主改進的通用智能體的重要步驟。本文研究LLMs推理階段計算量的擴展規律,重點回答以下問題:若允許LLM使用固定但可觀的推理階段計算量,其能在具有挑戰性的提示上提升多少性能?回答該問題不僅對LLMs\mathbf{LLMs}LLMs的可實現性能有啟示,還影響LLMs預訓練的未來方向以及如何權衡推理階段與預訓練階段的計算資源。盡管該問題重要,但鮮有研究嘗試理解各種測試時推理方法的擴展行為。此外,現有工作大多對這些策略給出了負面結果。本文分析兩種擴展測試時計算量的主要機制:(1)基于密集過程驗證器獎勵模型進行搜索;(2)根據測試時提示動態調整模型對響應的概率分布。我們發現,兩種情況下不同測試時計算量擴展方法的有效性均高度依賴提示的難度。這一觀察促使我們采用"計算最優"擴展策略,即根據每個提示動態分配測試時計算量以實現最有效利用。使用該計算最優策略,相比最佳N選1(best-of-N)基線,測試時計算量擴展效率可提升超過4倍。此外,在FLOPs匹配的評估中,我們發現對于某些問題,當較小基礎模型達到一定非零成功率時,測試時計算量可超越14倍參數量的更大模型。
1 引言
人類在面對困難問題時往往會花更長時間思考,以可靠地改進決策[9, 17, 18]。我們能否為當前的大型語言模型(LLMs)賦予類似能力?更具體地說,對于具有挑戰性的輸入查詢,能否使語言模型在測試時最有效地利用額外計算量,以提高響應的準確性?理論上,通過在測試時增加計算量,LLM應能超越其訓練時的能力。此外,這種測試時能力還可能為自主智能體和推理任務開辟新途徑[28, 34, 47]。例如,若預訓練模型規模可與推理階段計算量進行權衡,則可在需要較小設備端模型的場景中替代數據中心級LLM。通過額外推理計算自動生成改進的模型輸出,也為實現通用自改進算法提供了路徑,該算法可在減少人工監督的情況下運行。
此前研究測試時計算量的工作結果不一。一方面,部分研究表明當前LLM可通過測試時計算量提升輸出[4, 8, 23, 30, 48];另一方面,其他工作顯示這些方法在數學推理等復雜任務上的效果仍非常有限[15, 37, 43],盡管推理問題通常只需基于現有知識進行推斷,而非獲取新知識。這類矛盾結論促使需要系統分析不同測試時計算量擴展方法。
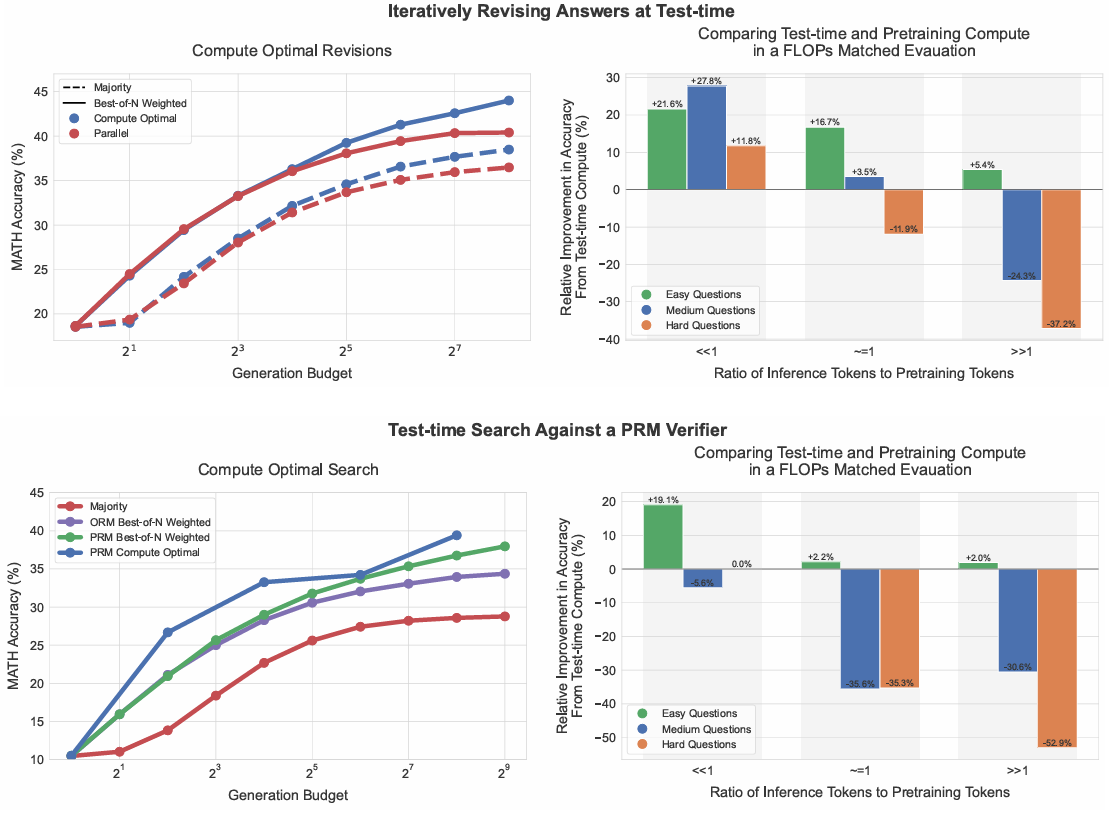
圖1 | 主要結果總結。左:迭代自優化(即修訂)與搜索的計算最優擴展。左側比較了PaLM 2-S*修訂模型的計算最優擴展策略與基線在修訂場景(上)和PRM搜索場景(下)的表現。可見在修訂場景中,標準最佳N選1(如"并行")與計算最優擴展的差距逐漸擴大,計算最優擴展可用4倍更少的測試計算量超越最佳N選1。類似地,在PRM搜索場景中,計算最優擴展早期顯著優于最佳N選1,部分點上用4倍更少計算量即可接近最佳N選1的表現。詳見第5、6節。右:測試時計算量與模型參數量擴展的對比。我們比較了計算最優測試時擴展的PaLM 2-Sˉ\bar{\mathrm{S}}Sˉ*模型與無額外測試時計算量的~\sim~ 14倍更大預訓練模型(如貪心采樣)的性能。考慮預訓練X token、推理Y token的場景。訓練更大模型會等比例增加兩者的FLOPs需求。若為較小模型分配額外測試時計算量以匹配更大模型的FLOPs需求,其準確性如何?可見在修訂場景(上),當Y?XY \ll XY?X時,測試時計算量通常優于額外預訓練。但隨著推理與預訓練token比例增加,測試時計算量在簡單問題上仍更優;而困難問題上預訓練更優。PRM搜索場景(下)也呈現類似趨勢。詳見第7節。
我們關注理解擴展測試時計算量的收益。最簡單且研究最充分的方法是最佳N選1采樣:從基礎LLM"并行"采樣N個輸出,并選擇經學習驗證器或獎勵模型評分最高的結果[7,22]。但該方法并非唯一利用測試時計算量改進LLM的途徑。通過修改響應的生成分布(例如讓基礎模型"順序"修訂原始響應[28]),或調整驗證器的使用方式(例如訓練基于過程的密集驗證器[22,45]并基于此搜索),可大幅提高測試時計算量的擴展能力,如本文所示。
為理解擴展測試時計算量的收益,我們在具有挑戰性的MATH[13]基準上開展實驗,使用專門微調的PaLM-2[3]模型進行錯誤答案修訂[28](如改進生成分布;第6節)或通過基于過程的獎勵模型(PRM)[22,45]驗證答案步驟的正確性(第5節)。兩種方法均表明,特定測試時計算策略的有效性高度依賴具體問題的性質和基礎LLM。例如,對于基礎LLM已能生成合理響應的簡單問題,允許模型通過預測N個修訂序列迭代優化初始答案(即修改生成分布),可能比并行采樣N個獨立響應更有效利用測試時計算量。另一方面,對于可能需要探索多種高層解題策略的困難問題,并行重新采樣獨立響應或基于過程獎勵模型的樹搜索,可能是更有效的測試時計算利用方式。這一發現表明需要部署自適應的"計算最優"策略來擴展測試時計算量,即根據提示動態選擇測試時計算利用方式,以實現最佳效果。我們還表明,基于基礎LLM視角的問題難度(第4節)可預測測試時計算量的有效性,從而實際構建這種計算最優策略。通過計算最優擴展,修訂和搜索場景下均可超越最佳N選1基線,同時僅使用約1/4的計算量(第5、6節)。
利用改進的測試時計算擴展策略,我們進一步探究測試時計算量在多大程度上可替代額外預訓練。我們對比了較小模型加測試時計算量與14倍更大預訓練模型的FLOPs匹配場景。發現對于簡單、中等難度問題,甚至部分困難問題(取決于預訓練和推理工作負載的具體條件),額外測試時計算量通常優于擴展預訓練。這表明與其單純擴展預訓練,某些場景下預訓練較小模型并應用測試時計算量更有效。但需注意,對于最具挑戰性的問題,測試時計算量的收益非常有限,此時額外預訓練計算量更有效,表明當前測試時計算擴展方法無法與預訓練擴展完全等價。總體而言,這表明即使采用較簡單的方法,擴展測試時計算量已可比擴展預訓練更優,且隨著測試時策略的成熟,收益將進一步提升。長遠來看,這暗示未來可減少預訓練FLOPs,增加推理階段FLOPs。
2 測試時計算的統一視角:提議者與驗證者
我們首先統一了利用測試時計算的方法,并分析了一些代表性技術。首先,我們從動態調整模型在給定提示下的預測分布這一角度,審視額外測試時計算的使用。理想情況下,測試時計算應修改分布,使生成結果優于直接從LLM采樣。一般來說,誘導LLM分布修改有兩種方式:(1)輸入層:通過向給定提示添加額外標記,使LLM基于這些標記調整分布;(2)輸出層:從標準語言模型采樣多個候選,并對這些候選進行修正。換言之,我們可以通過修改LLM自身誘導的提議分布(使其優于單純基于提示的條件分布),或使用事后驗證器/評分器對輸出進行修正。這一過程類似于從復雜目標分布中通過馬爾可夫鏈蒙特卡洛(MCMC)[2]采樣,但結合了簡單的提議分布和評分函數。通過調整輸入標記直接修改提議分布,以及使用驗證器,構成了我們研究的兩個獨立方向。
修改提議分布。改進提議分布的一種方法是通過對抗強化學習(RL)的微調方法(如STaR或ReST,EM[35,50])直接優化模型在特定推理任務上的表現。需要注意的是,這些技術不依賴額外輸入標記,而是通過微調模型來誘導更優的提議分布。相反,自我批判(self-critique)[4,8,23,30]等方法使模型在測試時通過迭代批判和修正自身輸出,從而改進提議分布。由于直接提示現成模型無法有效實現測試時修正,我們專門微調模型在復雜推理場景中迭代修正答案。為此,我們采用基于最佳N選1(Best-of-N)引導改進的微調方法[28],利用在策略數據(on-policy data)進行微調。
優化驗證器。在提議分布與驗證器的抽象框架中,驗證器用于從提議分布中聚合或選擇最優答案。最典型的方式是使用最佳N選1采樣:采樣N個完整解決方案,然后通過驗證器選擇最優解[7]。但該方法可進一步改進,例如訓練基于過程的驗證器[22](即過程獎勵模型,PRM),其預測解決方案中每一步的正確性,而非僅評估最終答案。利用這些逐步預測,我們可以在解決方案空間中執行樹搜索,相比簡單的最佳N選1[6,10,48],可能實現更高效、更有效的驗證器搜索。
3 如何最優擴展測試時計算
基于對各類方法的統一分析,我們現在希望理解如何最有效地利用測試時計算來提升語言模型在給定提示下的性能。具體而言,我們試圖回答以下問題:
問題設定
給定一個提示和測試時計算預算,我們需要在上述抽象框架下選擇不同的測試時計算利用方式。不同方法對具體問題的有效性可能差異顯著。如何為給定提示確定最有效的測試時計算利用方式?這種方法與直接使用更大的預訓練模型相比效果如何?
無論是修正提議分布還是基于驗證器搜索,均存在多個可調整的超參數以決定測試時計算預算的分配方式。例如,當使用微調后的修正模型作為提議分布、ORM作為驗證器時,我們可以將全部測試時計算預算用于并行生成N個獨立樣本并執行最佳N選1,或按順序生成N個修正版本并使用ORM選擇最優答案,或在兩者之間取得平衡。直覺上,我們可能認為“簡單”問題更適合修正,因為模型的初始樣本更可能接近正確方向,只需進一步細化;而困難問題可能需要探索不同的高層解題策略,因此并行獨立采樣多次可能更優。
對于驗證器,我們還可選擇不同的搜索算法(如束搜索、前瞻搜索、最佳N選1),其性能可能因驗證器和提議分布的質量而異。更復雜的搜索程序可能在更難的問題上比簡單的最佳N選1或多數投票基線更有效。
3.1 測試時計算最優擴展策略
因此,我們希望為給定問題選擇最優的測試時計算預算分配方式。為此,對于任意利用測試時計算的方法(如本文的修正和驗證器搜索,或其他方法),我們定義“測試時計算最優擴展策略”為:在給定提示下,通過調整超參數使測試時計算預算的分配能最大化性能收益的策略。形式化地,設Target?(θ,N,q)\operatorname{Target}(\theta, N, q)Target(θ,N,q)為模型在給定提示qqq、測試時計算超參數θ\thetaθ和預算NNN時誘導的自然語言輸出分布。我們希望選擇超參數θ\thetaθ,使該分布在給定問題上的準確率最高。正式表述為:
θq,a?(q)?(N)=argmax?θ(Ey~Target?(θ,N,q)[1y=y?(q)]),\begin{array}{r}{\boldsymbol{\theta}_{q,a^{*}(q)}^{*}\big(N\big)=\operatorname*{arg max}_{\boldsymbol{\theta}}\left(\mathbb{E}_{\boldsymbol{y}\sim\operatorname*{Target}\left(\boldsymbol{\theta},N,q\right)}\left[\mathbb{1}_{\boldsymbol{y}=\boldsymbol{y}^{*}(q)}\right]\right),}\end{array}θq,a?(q)??(N)=argmaxθ?(Ey~Target(θ,N,q)?[1y=y?(q)?]),?
其中y?(q){\boldsymbol{y}}^{*}({\boldsymbol{q}})y?(q)表示提示qqq的地面真實正確響應,θq,y?(q)?(N)\boldsymbol{\theta}_{q,y^{*}\left(q\right)}^{*}\big(N\big)θq,y?(q)??(N)表示在計算預算NNN下,針對問題qqq的最優測試時計算擴展策略。
3.2. 基于問題難度的計算最優擴展估計
為有效分析第2節中討論的不同機制(如提議分布與驗證器)的測試時擴展特性,我們將最優策略θq,y?(q)?(N)\boldsymbol{\theta}_{q,y^{*}\left(q\right)}^{*}\big(N\big)θq,y?(q)??(N)近似為提示的某個統計量的函數。該統計量估計了提示的難度。計算最優策略定義為該難度的函數。盡管這只是對式(1)中問題的近似解,我們發現它仍能顯著提升性能,優于隨機或均勻分配推理計算預算的基線策略。
我們的難度估計將給定問題劃分為五個難度等級。通過驗證集上的離散難度分類,我們可以為給定測試時計算預算估計θq,y?(q)?(N)\boldsymbol{\theta}_{q,y^{*}\left(q\right)}^{*}\big(N\big)θq,y?(q)??(N),并將該策略應用于測試集。具體而言,我們獨立為每個難度等級選擇性能最優的測試時計算策略。因此,問題難度作為設計計算最優策略的充分統計量。
定義問題難度。遵循Lightman等人[22]的方法,我們基于基礎LLM定義問題難度。具體來說,我們將模型在測試集每個問題上的pass@1率(通過2048個樣本估計)劃分為五個分位數,分別對應遞增的難度等級。我們發現,這種基于模型的難度分箱比MATH數據集中的手工標注難度更能預測測試時計算的有效性。
需注意,上述難度評估假設可訪問地面真實正確性檢查函數,而實際部署時我們無法知曉測試提示的答案。因此,基于難度的計算最優策略需首先評估問題難度,再利用對應策略解決。為此,我們通過模型預測的難度近似真實難度:對每個問題的2048個樣本,基于學習驗證器的平均最終答案得分(而非地面真實正確性)執行相同分箱程序。我們將此設定稱為“模型預測難度”,而依賴地面真實正確性的設定稱為“oracle難度”。
盡管模型預測難度避免了依賴地面真實標簽,但其評估仍需額外推理計算。不過,此一次性推理成本可包含在執行推理策略的總成本中(例如,使用驗證器時,可復用相同推理計算進行搜索)。更一般地,這類似于強化學習中的探索-利用權衡:實際部署時需平衡評估難度與應用最優策略的計算開銷。這是未來研究的關鍵方向(見第8節),而我們的實驗為簡化未考慮此成本,因我們目標僅是展示有效分配測試時計算的初步結果。
為避免使用同一測試集計算難度分箱和選擇最優策略的混淆因素,我們對測試集的每個難度分箱采用兩折交叉驗證。在一折上選擇性能最優的策略,并在另一折上評估該策略的性能,反之亦然,最終對兩折結果取平均。
4 實驗設置
我們首先概述實驗設置,包括多種驗證器設計選擇和提議分布的分析,后續章節將呈現分析結果。
數據集。我們聚焦于模型已掌握所需基本知識、主要挑戰在于從該知識中推導(復雜)推理的場景。為此,我們選擇MATH[13]基準,該數據集包含高中競賽級別的數學問題,難度范圍廣泛。所有實驗均采用Lightman等人[22]使用的數據集劃分:12k訓練問題和500測試問題。
模型。我們使用PaLM 2-S*[3](Codey)基礎模型進行分析。該模型代表了當代LLMs的典型能力,因此我們認為 findings可推廣至類似模型。更重要的是,該模型在MATH上達到非零性能且未飽和,適合作為測試平臺。
5 通過驗證器擴展測試時計算
本節分析如何通過優化驗證器盡可能有效地擴展測試時計算。我們研究基于過程驗證器(PRM)的測試時搜索方法,并分析不同方法的測試時計算擴展特性。
5.1 訓練適用于搜索的驗證器
PRM訓練。原始PRM訓練[22,42]依賴人工標注數據。盡管Lightman等人[22]發布了PRM訓練數據(PRM80Ok),但我們發現該數據效果有限。即使通過簡單策略(如最佳N選1)也可輕易利用基于此數據訓練的PRM。推測原因可能是該數據集的GPT-4生成樣本與我們的PaLM 2模型存在分布偏移。為避免昂貴的人工標注,我們采用Wang等人[45]的方法,通過蒙特卡洛展開估計每步正確性,無需人工標簽即可訓練PRM。具體而言,PRM的每步預測對應基礎模型采樣策略的回報到值估計(reward-to-go),與近期工作[31,45]一致。我們還對比了ORM基線(附錄F),但發現PRM始終更優。因此,本節所有搜索實驗均使用PRM模型。PRM訓練細節見附錄D。
答案聚合。測試時,基于過程的驗證器可對基礎模型采樣的多組解進行逐步評分。為通過PRM選擇最佳N選1答案,需設計聚合函數將各答案的逐步評分整合為最終分數。具體實現如下:
逐步聚合。我們不采用乘積或最小值聚合[22,45],而是直接使用PRM對最后一步的預測作為整題分數。實驗表明該方法在所有研究過的聚合方法中表現最佳(見附錄E)。
答案間聚合。我們遵循Li等人[21]的“最佳N選1加權”策略,而非標準最佳N選1。該方法對所有具有相同最終答案的解進行邊際化,選擇總評分最高的最終答案。
5.2 基于PRM的搜索方法
我們通過搜索方法優化PRM在測試時的表現。研究三種從少樣本提示的基礎LLM采樣輸出的搜索策略(見附錄G),圖2為示意圖。
最佳N選1加權。從基礎LLM獨立采樣N個答案,根據PRM的最終答案評分選擇最優解。
束搜索(Beam Search)。通過束搜索優化PRM的逐步預測。實現類似BFS-V[10,48],具體步驟如下:
- 采樣N個初始預測作為解決方案的第一步
- 根據PRM的逐步回報到值估計(對應稀疏獎勵設置下的總獎勵)對生成步驟評分
- 保留前NM\frac{N}{M}MN?個最高分步驟
- 對每個候選步驟采樣M個下一步提案,得到總計N/M×MN{\big/}M\times MN/M×M個候選前綴,重復步驟2-4
搜索持續至解決方案結束或達到最大展開輪數(本實驗設為40)。最終保留N個候選答案,通過最佳N選1加權選擇最終答案。
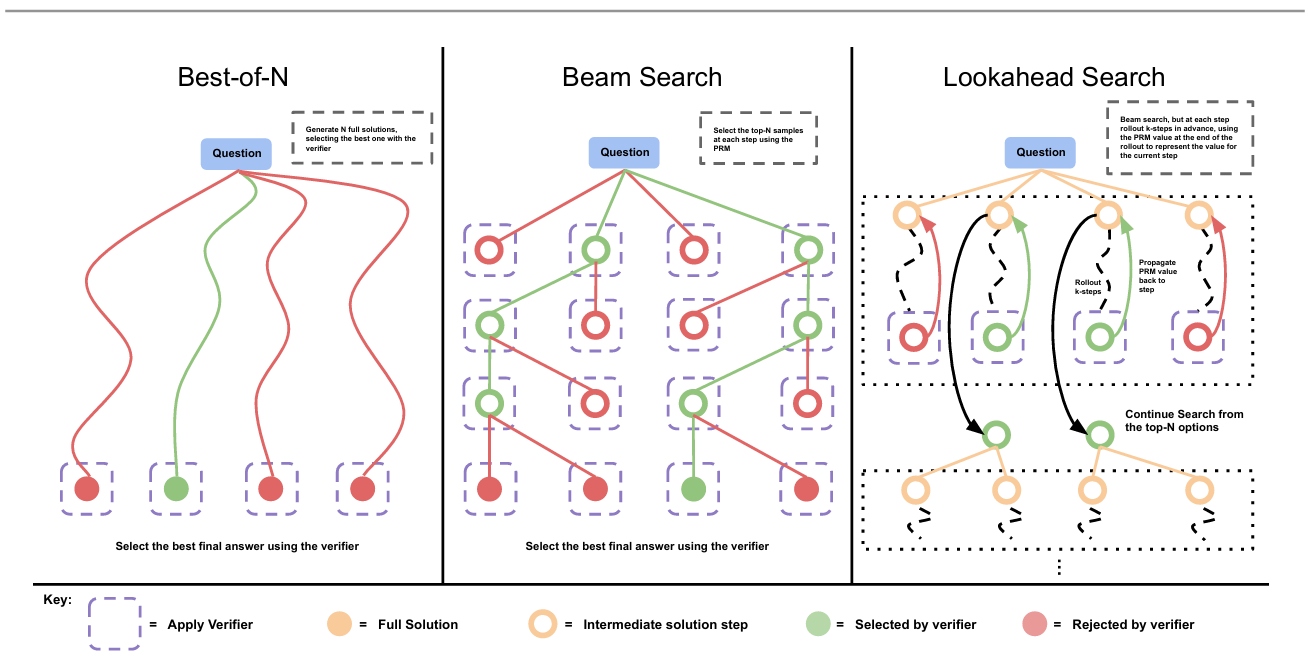
圖2 | 不同PRM搜索方法對比。左:最佳N選1采樣N個完整答案,根據PRM最終評分選擇最優解。中:束搜索每步采樣N個候選,根據PRM選擇前M個繼續搜索。右:前瞻搜索在束搜索基礎上擴展,利用k步前瞻評估保留步驟,需更多計算。
前瞻搜索(Lookahead Search)。修改束搜索的步驟評估方式,通過前瞻展開提高PRM值估計的準確性。具體而言,在束搜索的每一步,不直接使用當前步驟的PRM評分選擇候選,而是執行模擬展開:以溫度0采樣最多k步(若提前到達解終點則停止),使用展開末尾的PRM預測評分當前步驟。換言之,束搜索可視為前瞻搜索的特例(k=0)。若PRM準確,增加k可提高逐步值估計的準確性,但需額外計算。此版本前瞻搜索是MCTS[38]的特例,去除了MCTS中用于探索的隨機元素(因PRM已訓練完成且凍結),這些元素對值函數學習(已通過PRM完成)作用有限,測試時更需利用而非探索。因此,前瞻搜索可代表MCTS類方法在測試時的應用。
5.3 分析結果:驗證器搜索的測試時擴展
本節比較不同搜索算法,并識別搜索方法的提示難度依賴型計算最優擴展策略。
搜索算法對比。我們首先掃描不同搜索設置。除標準最佳N選1外,掃描束搜索的兩個主參數(束寬M和前瞻步數k)。在最大預算256下,掃描以下設置:
- 束寬設為N{\sqrt{N}}N?的束搜索,N為生成預算
- 固定束寬4的束搜索
- 對上述兩種束搜索設置應用k=3的前瞻搜索
- 對設置1應用k=1的前瞻搜索
為公平比較生成預算,我們定義生成成本:基礎LLM采樣一個答案計為一次生成。束搜索和最佳N選1的生成預算分別對應束寬和N。前瞻搜索需額外計算:每步搜索需模擬k步前瞻,因此成本定義為N×(k+1)N\times(k+1)N×(k+1)次采樣。
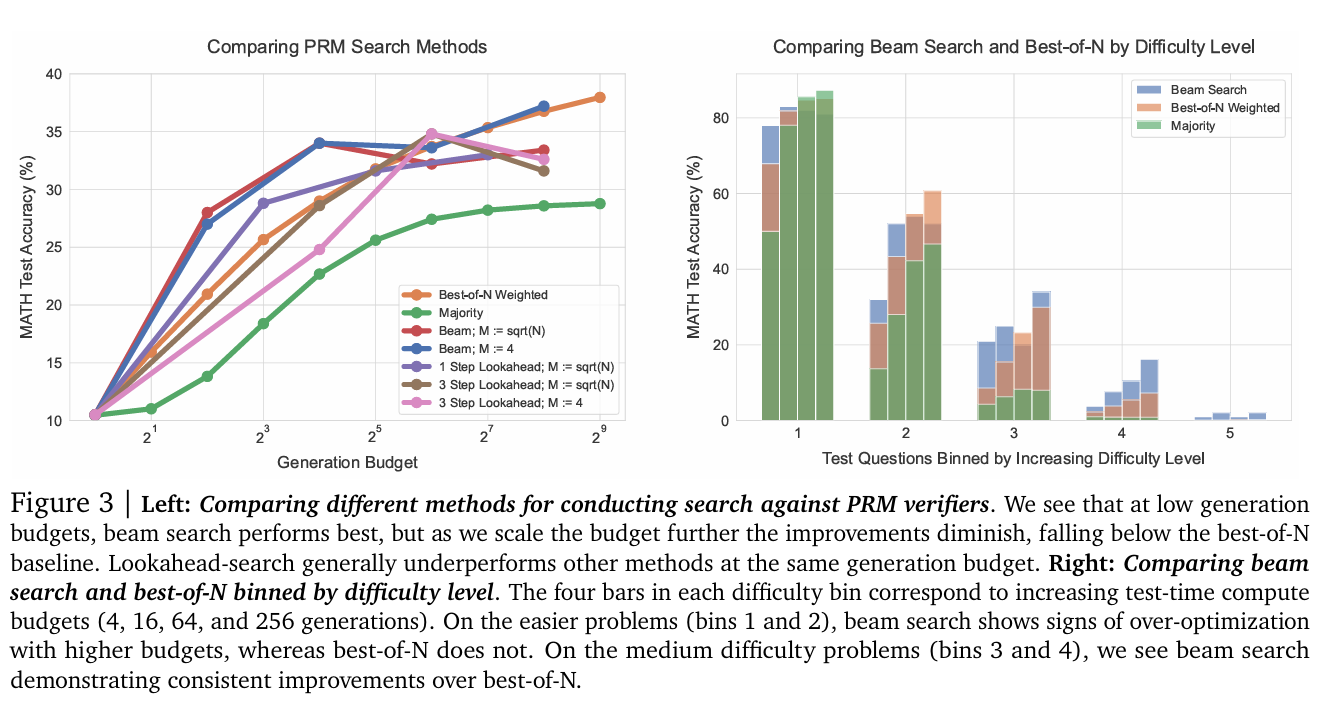
結果。如圖3(左)所示,小預算下束搜索顯著優于最佳N選1;但預算增大時,束搜索的改進大幅減弱,甚至低于最佳N選1基線。同一預算下,前瞻搜索通常表現更差,可能因模擬前瞻展開引入額外計算。搜索的收益遞減可能源于PRM預測的過度利用。例如,部分案例(如圖29)中,搜索導致模型在解末尾生成低信息的重復步驟;其他案例中,過度優化的搜索可能生成僅含1-2步的過短解。這解釋了最強搜索方法(前瞻搜索)表現最差的原因。附錄M列舉了搜索發現的此類案例。
搜索改進的問題類型。為理解計算最優搜索策略,我們按難度分箱分析。比較束搜索(M=4)與最佳N選1。如圖3(右),高生成預算下,束搜索與最佳N選1總體性能相近,但難度分箱分析揭示差異趨勢:
- 易問題(難度1、2):更強的優化方法(束搜索)隨預算增加性能下降,表明PRM信號被過度利用(類似過擬合)。
- 中等難度問題(難度3、4):束搜索持續優于最佳N選1。
- 最難問題(難度5):所有方法均無明顯進展。
此發現符合直覺:易問題中,驗證器對正確性的評估大多準確,束搜索進一步放大驗證器學習的虛假特征,導致性能下降;難問題中,基礎模型初始采樣正確答案的概率低,搜索可引導模型更頻繁生成正確答案。
計算最優搜索策略。上述結果表明,問題難度是預測最優搜索策略的有效統計量,且最優策略隨難度顯著變化。圖4可視化“計算最優”擴展趨勢:各難度等級下性能最優的搜索策略。可見,低生成預算下,無論使用真實難度(oracle)還是預測難度,計算最優策略均可用至多4倍更少的測試計算(如16代64)接近最佳N選1性能;高預算下,預測難度的部分收益減弱,但真實難度分箱仍顯示最優擴展的持續改進。此結果證明,搜索時自適應分配測試計算可帶來性能增益。
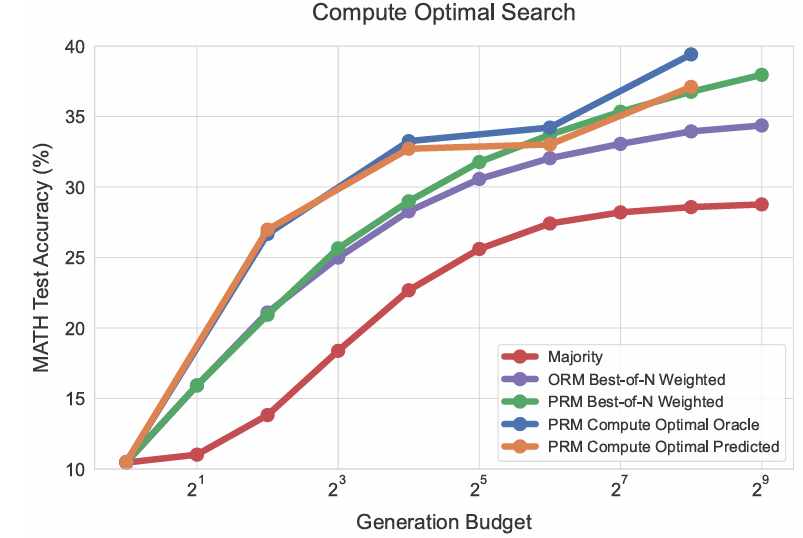
圖4 | PRM搜索下計算最優測試計算分配與基線對比。通過按問題難度擴展測試計算,計算最優策略可用至多4倍更少的測試計算(如16代64)接近最佳N選1性能。“計算最優oracle”指基于真實正確性信息的難度分箱,“計算最優predicted”指基于PRM預測的難度分箱。兩曲線基本重合。
驗證器計算最優擴展的啟示
驗證器搜索方法的有效性高度依賴計算預算和問題難度。具體而言,束搜索在難問題和低預算下更有效,最佳N選1在易問題和高預算下更優。此外,通過按問題難度和測試計算預算選擇最優搜索設置,計算最優策略可用至多4倍更少的測試計算接近最佳N選1性能。
6 優化提議分布
此前我們研究了基于驗證器的搜索方法的測試時計算擴展特性。本節轉向分析修改提議分布(第2節)的擴展特性。具體而言,我們使模型能夠迭代修正自身答案,動態改進測試時的分布。直接提示現有LLMs修正自身錯誤對推理問題的性能提升效果有限[15]。因此,我們基于Qu等人[28]的方法,結合針對我們場景的修改,微調語言模型以迭代修正自身答案。首先描述如何訓練和使用通過順序關聯先前嘗試來優化提議分布的修正模型,隨后分析修正模型在推理時的擴展特性。
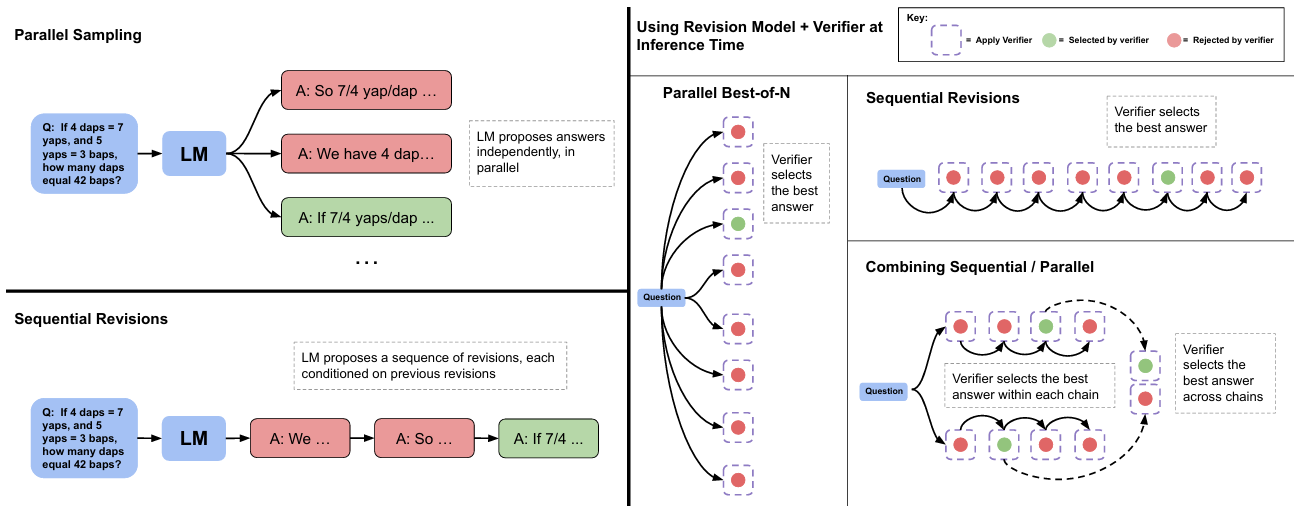
圖5 | 并行采樣(如最佳N選1)與順序修正對比。左:并行采樣獨立生成N個答案;順序修正逐個生成答案,每個答案基于前序嘗試。右:在順序和并行場景中,均可使用驗證器選擇最佳答案(如通過加權最佳N選1)。也可分配部分預算給并行采樣,部分給順序修正,實現兩種策略的組合。此時先用驗證器在每條順序鏈內選最佳答案,再跨鏈選最優。
6.1 實驗設置:訓練與使用修正模型
我們的修正模型微調流程與[28]類似,但存在關鍵差異。微調需要包含錯誤答案序列后接正確答案的軌跡,以便通過監督學習(SFT)優化模型。理想情況下,正確答案應與上下文中的錯誤答案相關聯,從而有效訓練模型隱式識別上下文示例中的錯誤,并通過編輯修正錯誤,而非忽略上下文示例并從頭重試。
生成修正數據。Qu等人[28]的多輪展開(multi-turn rollout)方法雖有效,但因計算成本問題在我們基礎設施中不可行。因此,我們以較高溫度并行采樣64個響應,事后從中構建多輪展開軌跡。具體而言,遵循[1]的方法,將每個正確答案與該集合中的錯誤答案序列配對作為上下文,構建多輪微調數據。上下文中最多包含四個錯誤答案,具體數量從0到4的均勻分布中隨機采樣。我們使用字符編輯距離度量優先選擇與最終正確答案相關的錯誤答案(見附錄H)。雖然詞元編輯距離并非完美的相關性度量,但該啟發式方法足以關聯上下文中的錯誤答案與正確目標答案,從而訓練有意義的修正模型,而非隨機配對無關聯的響應。
推理時使用修正。給定微調后的修正模型,可在測試時從模型中采樣一系列修正。盡管我們的修正模型僅訓練過最多四個上下文答案,但可通過截斷上下文至最近四個修正響應來采樣更長鏈。圖6(左)顯示,隨著修正鏈長度增加,模型在每一步的pass@1逐漸提升,表明模型能夠有效學習利用上下文中的先前答案錯誤進行改進,甚至超越訓練時的四步限制。
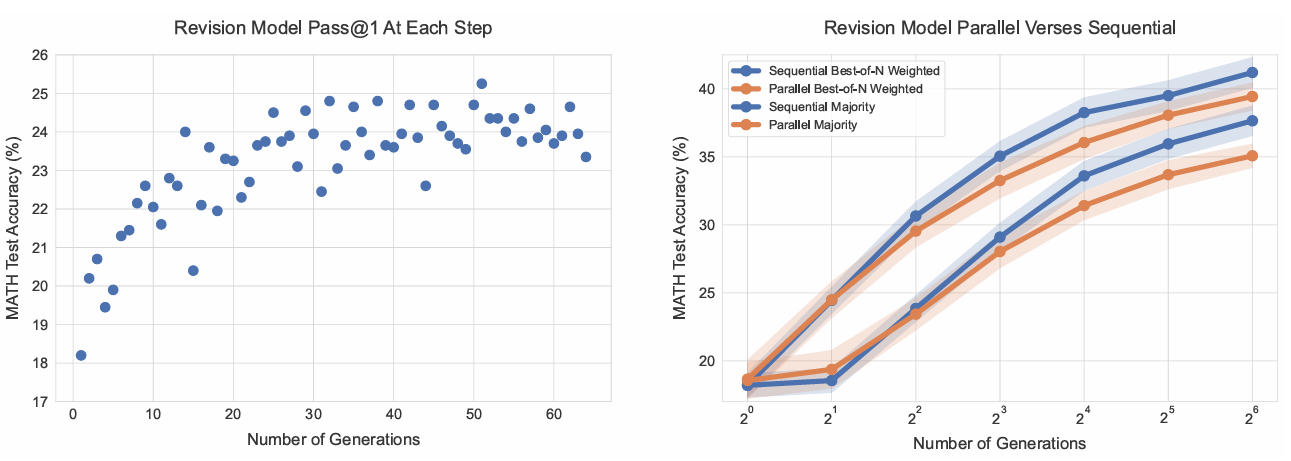
圖6 | 左:修正模型在每一步的pass@1。經過每一步修正,pass@1逐漸提升,甚至超過訓練時的四步限制。我們通過平均測試集每個問題的4條長度為64的修正軌跡的性能來估計每步pass@1。右:修正模型的順序與并行采樣對比。比較從修正模型并行生成N個初始答案與順序生成N個修正的性能。當使用驗證器或多數投票選擇答案時,順序生成略優于并行生成。
需注意,推理時存在分布偏移:模型僅在上下文包含錯誤答案的情況下訓練,但測試時上下文可能包含正確答案。此時,模型可能在下一步修正中將正確答案轉為錯誤答案。類似Qu等人[28],我們發現約38%的正確答案通過樸素方法被修正模型轉為錯誤答案。因此,我們采用順序多數投票或基于驗證器的選擇機制,從模型生成的修正序列中選出最正確的答案(見圖5),以生成最終答案。
對比實驗。為測試通過修正優化提議分布的有效性,我們公平比較順序采樣N個修正與并行采樣N個問題嘗試的性能。圖6(右)顯示,無論使用基于驗證器還是多數投票的選擇機制,順序采樣均略優于并行采樣。
6.2 分析結果:修正的測試時擴展
此前觀察到順序采樣優于并行采樣,但兩者特性可能不同。并行采樣更似全局搜索,可能覆蓋多種完全不同的解題方法(如不同候選采用不同高層策略)。順序采樣則更似局部優化,修正已部分正確的響應。由于兩者互補,應通過分配部分推理預算給并行采樣(如N\sqrt{N}N?)、部分給順序修正(如N\sqrt{N}N?)來平衡。下文將展示順序與并行采樣的計算最優比率存在性,并基于問題難度分析其優劣。
順序與并行計算的權衡。為理解如何最優分配順序與并行計算,我們掃描不同比率。圖7(左)顯示,在固定生成預算下,存在使準確率最大的理想順序-并行比率。圖7(右)進一步按難度分箱分析,使用驗證器選擇時,簡單問題在全順序計算下表現最佳,而困難問題需平衡順序與并行計算。
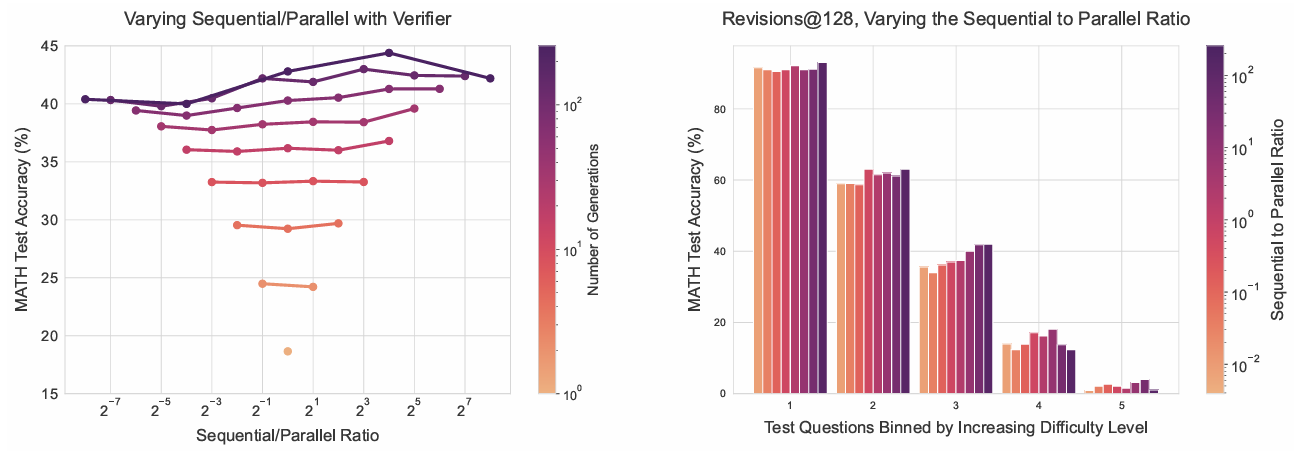
圖7 | 左:變化順序修正與并行采樣的預算分配比率。每條線代表固定生成預算下比率變化的表現,使用驗證器選擇答案。可見增加順序修正傾向優于更多并行計算,但高預算下存在平衡兩者比率的理想點。右:生成預算128下按難度分箱的變化順序-并行比率表現。使用驗證器選擇時,簡單問題在全順序計算下最佳,困難問題需平衡順序與并行計算。
計算最優修正策略。鑒于順序與并行采樣的有效性依賴問題難度,可按難度分箱選擇理想比率。圖8展示使用真實難度(oracle)與預測難度時,計算最優策略的結果。兩種情況下,通過修正優化提議分布均可顯著提升測試時計算擴展效率。高生成預算下,并行采樣性能趨于平穩,而計算最優策略持續改進。無論真實還是預測難度,計算最優策略均可用至多4倍更少測試計算(如64樣本代256)超越最佳N選1基線。總體表明,通過按提示調整提議分布,可更高效擴展測試時計算。
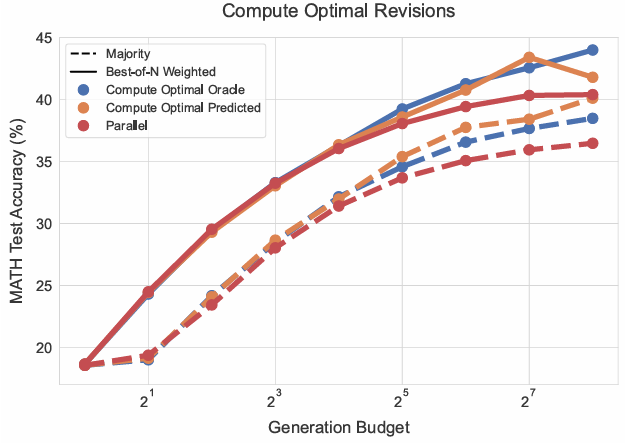
修正提議分布的計算最優擴展啟示
順序(如修正)與并行(如最佳N選1)測試時計算存在權衡,理想比率依賴計算預算和問題難度。簡單問題更適合全順序計算,困難問題需平衡順序與并行計算。通過按問題難度和測試計算預算選擇最優設置,計算最優策略可用至多4倍更少測試計算超越并行最佳N選1基線。
7 綜合分析:交換預訓練與測試時計算
此前我們看到,額外測試時計算可通過優化提議分布或搜索驗證器,使模型表示比基礎LLM更復雜的分布,從而提升性能。現假設:這種表示復雜分布的靈活性是否意味著測試時計算可替代更高容量模型或更多預訓練FLOPs?本節研究此問題的程度。我們提出以下問題:
問題:交換預訓練與測試時計算
假設模型預訓練消耗XXX FLOPs,計劃推理消耗YYY FLOPs。若需通過增加總FLOPs預算至M(X+Y)M(X+Y)M(X+Y)(即預訓練和推理總FLOPs為M(X+Y)M(X+Y)M(X+Y))來提升性能,應將FLOPs用于增加預訓練計算還是額外測試時計算?
增加預訓練FLOPs需決定是擴展數據還是參數[14]。我們聚焦參數擴展且訓練數據量固定的設置(類似開源LLaMA系列[41]),此為典型預訓練擴展方式,暫不分析數據與參數均衡擴展的預訓練計算最優擴展[29],留待未來工作。
定義FLOPs交換率。預訓練FLOPs近似為X=6NDpretrainX=6ND_{\text{pretrain}}X=6NDpretrain?[14],推理FLOPs為Y=2NDinferenceY=2ND_{\text{inference}}Y=2NDinference?[29],其中NNN為模型參數量,DpretrainD_{\text{pretrain}}Dpretrain?為預訓練詞元數,DinferenceD_{\text{inference}}Dinference?為推理生成詞元數。若參數擴展MMM倍,預訓練和推理FLOPs(因更大模型的貪心解碼成本)均增加MMM倍(總FLOPs為M(X+Y)M(X+Y)M(X+Y))。
為用小模型的測試時計算匹配大模型的FLOPs,需將小模型推理計算擴展M+3(DpretrainDinference)(M?1)\begin{array}{r}M+3\left(\frac{D_{\text{pretrain}}}{D_{\text{inference}}}\right)(M-1)\end{array}M+3(Dinference?Dpretrain??)(M?1)?倍。測試時計算可擴展量依賴比率DpretrainDinference\frac{D_{\text{pretrain}}}{D_{\text{inference}}}Dinference?Dpretrain??,其倒數記為R=DinferenceDpretrainR=\frac{D_{\text{inference}}}{D_{\text{pretrain}}}R=Dpretrain?Dinference??。不同場景下RRR差異顯著:大規模生產場景中,推理詞元數可能遠超預訓練(R?1R \gg 1R?1);而自我改進場景中,測試時計算用于優化模型,推理詞元數可能遠少于預訓練(R?1R \ll 1R?1)。
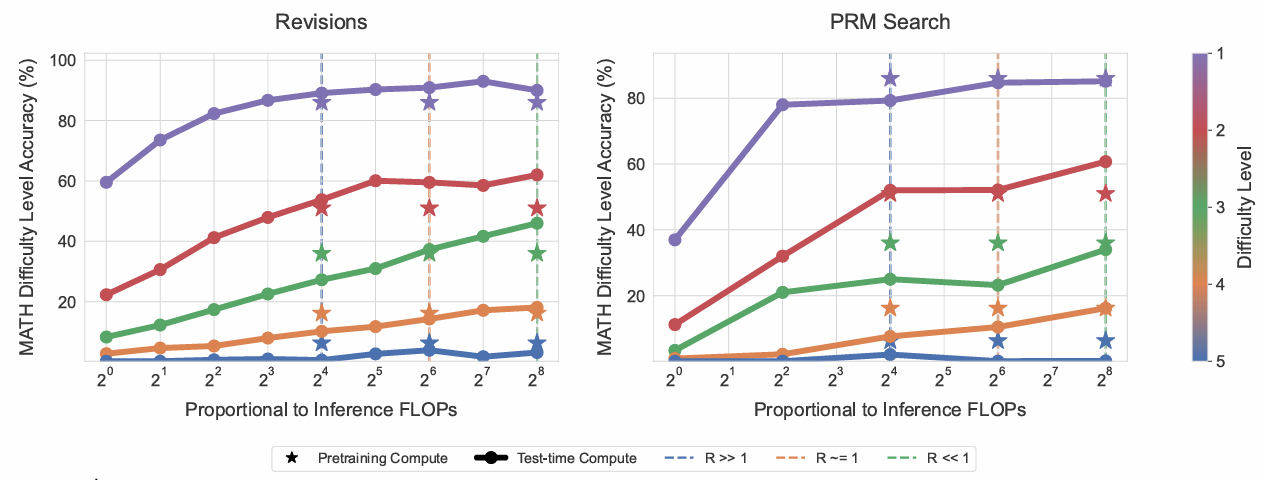
圖9中,我們比較計算最優策略與14倍參數大模型在三種RRR值(0.16[R?1R \ll 1R?1], 0.79[R~1R \sim 1R~1], 22[R?1R \gg 1R?1])下的表現。若僅遇困難問題(難度4/5)或RRR較大(高推理負載),預訓練通常更有效(星標在線上方);若主要為簡單或中等難度問題(難度1/2/3,有時4)或RRR較小(低推理負載,如自我改進管道),測試時計算更優。
交換預訓練與測試時計算的啟示
測試時與預訓練計算并非1:1可交換。簡單/中等難度問題(模型能力范圍內)或低推理負載場景下,測試時計算可輕易替代額外預訓練;困難問題(超出基礎模型能力)或高推理負載場景下,預訓練更有效。
8 討論與未來工作
本研究系統分析了通過搜索驗證器或優化提議分布來擴展測試時計算的有效性,重點關注數學推理。發現方法有效性高度依賴問題難度(從基礎模型能力視角)。由此引入“計算最優”測試時計算擴展概念,即根據提示動態調整策略以在給定預算下提升性能。采用此策略可使測試時計算擴展效率提升2?42-42?4倍。在FLOPs匹配場景中,首次證明簡單方法(如修正和搜索)的測試時計算在特定提示下可超越預訓練FLOPs投入。但研究仍存局限,未來工作可從以下方面改進:
進一步優化測試時計算擴展。本研究聚焦驗證器和提議分布(通過修正)的擴展,雖在修正中結合驗證器(第6節),但未嘗試PRM樹搜索與修正的組合,也未研究如批判-修正[23]等其他技術。未來工作應探索多種方法的組合以提升測試時計算擴展。此外,當前方法在困難問題上的增益有限,需開發新策略突破此限制。
快速評估問題難度。我們使用問題難度作為計算最優策略的充分統計量,雖有效但評估難度需額外測試時計算。未來工作可探索更高效的難度估計方法(如預訓練或微調模型直接預測問題難度),或動態切換難度評估與解題。
測試時與訓練時計算的交織。本研究僅關注測試時計算擴展及其與預訓練的權衡,但未來可設想將額外測試時計算的輸出蒸餾回基礎LLM,構建開放域自然語言的自改進循環。為此,需擴展當前發現,研究測試時計算的輸出如何用于改進基礎模型。
附錄
A. 相關研究
語言模型推理。近年來,語言模型在挑戰性數學推理任務上的性能迅速提升[20,22,25,32,39]。這些改進可歸因于四個主要因素:1)在大量數學相關語料庫上持續預訓練[20,22,32,39];2)通過針對特定推理任務的強化學習微調[32,35,49,50]或使模型能夠迭代批判并修正自身答案[4,8,23,30],從而優化LLM的提議分布;3)通過微調驗證器[6,7,10,22,40,42,45,48]使LLM受益于額外測試時計算。本研究基于第二和第三類研究,分析測試時計算擴展在以下兩方面的優化程度:1)優化LLM的提議分布;2)基于驗證器進行搜索。
分析測試時計算擴展。Jones[16]此前研究了蒙特卡洛樹搜索在棋盤游戲Hex中訓練時與測試時計算的權衡。我們則聚焦于全尺度語言模型數學推理問題的分析。Villalobos和Atkinson[44]的綜述分析了多領域的訓練與推理計算權衡,但其語言模型分析多集中于已知真實答案的場景。相比之下,我們關注真實答案未知的場景。此外,強化學習領域已提出MCTS[19]等方法,旨在平衡測試時與訓練時計算以實現迭代自博弈。本研究成果可助力開發適用于開放域自然語言的類似算法。
通過測試時計算增強LLM。除驗證器和修正外,多項研究提出了使LM利用測試時計算進行推理的替代方法。例如,Wang等人[46]通過分層假設搜索實現歸納推理能力。相關研究還提出在測試時為語言模型配備工具[11,26,27],顯著提升下游任務性能。最后,若干研究提出了無監督學習思維token的方法[12,51],使模型更有效利用采樣更長序列帶來的額外測試時計算。本研究聚焦測試時計算擴展的兩種主要機制(驗證器與修正),但分析方法(如基于問題難度的計算最優擴展)原則上可應用于其他測試時計算擴展方法,我們認為這是未來研究的有趣方向。
B. 額外修正結果
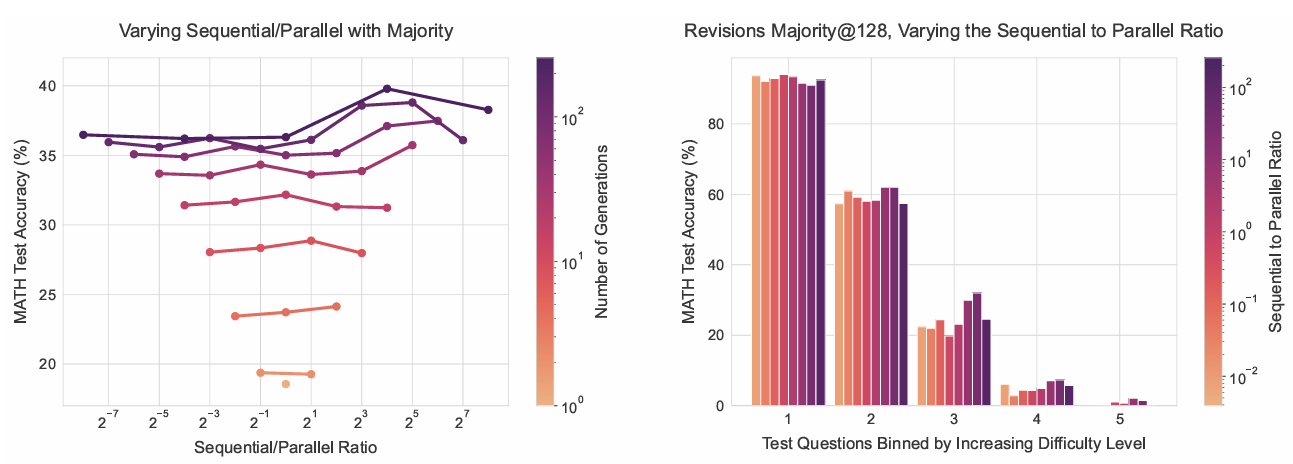
圖10展示了使用PaLM 2-S*修正模型進行多數選擇的結果。多數選擇下,趨勢與圖7中驗證器選擇的結果類似。
C. 無監督難度分箱
我們通過平均2048個樣本的PRM最終答案評分來計算無真實答案的難度分箱,從而獲得對應問題的價值估計。隨后將測試集每個問題的價值估計分為五等分(采用與真實難度分箱相同的流程),稱為“預測難度”而非“真實難度”。此流程成本極高,因需生成大量樣本。盡管分析中未計入此成本,但實際生產場景中可能存在問題。更高效的方法是微調模型直接預測問題正確性,本研究未探索此方向,留待未來研究更廉價的難度估計方法。
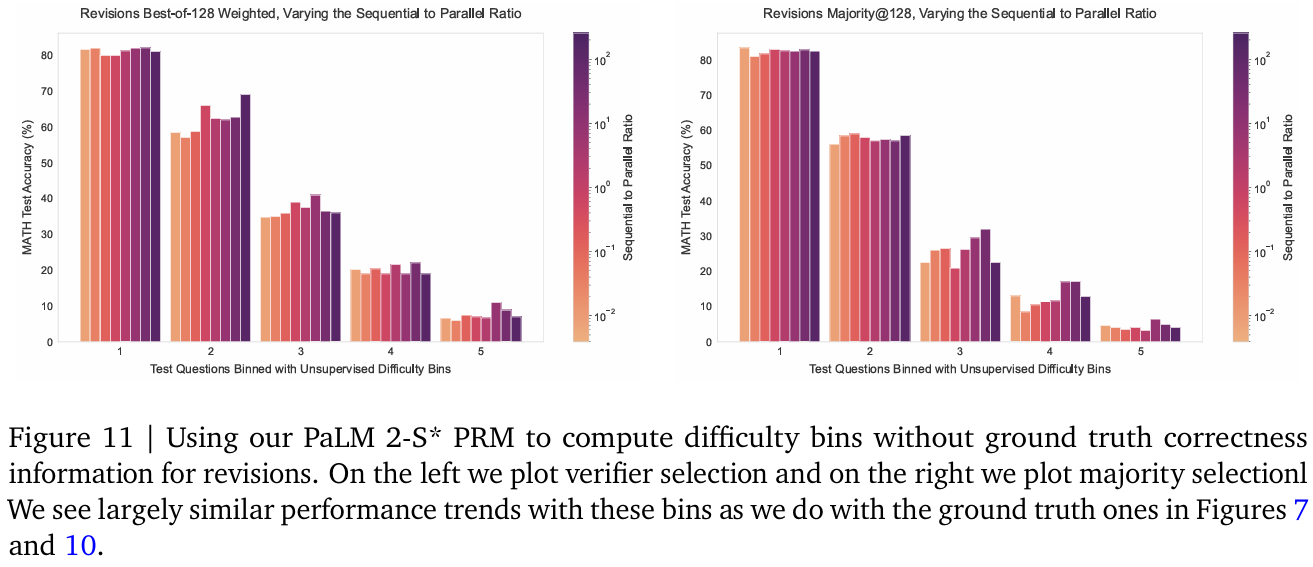
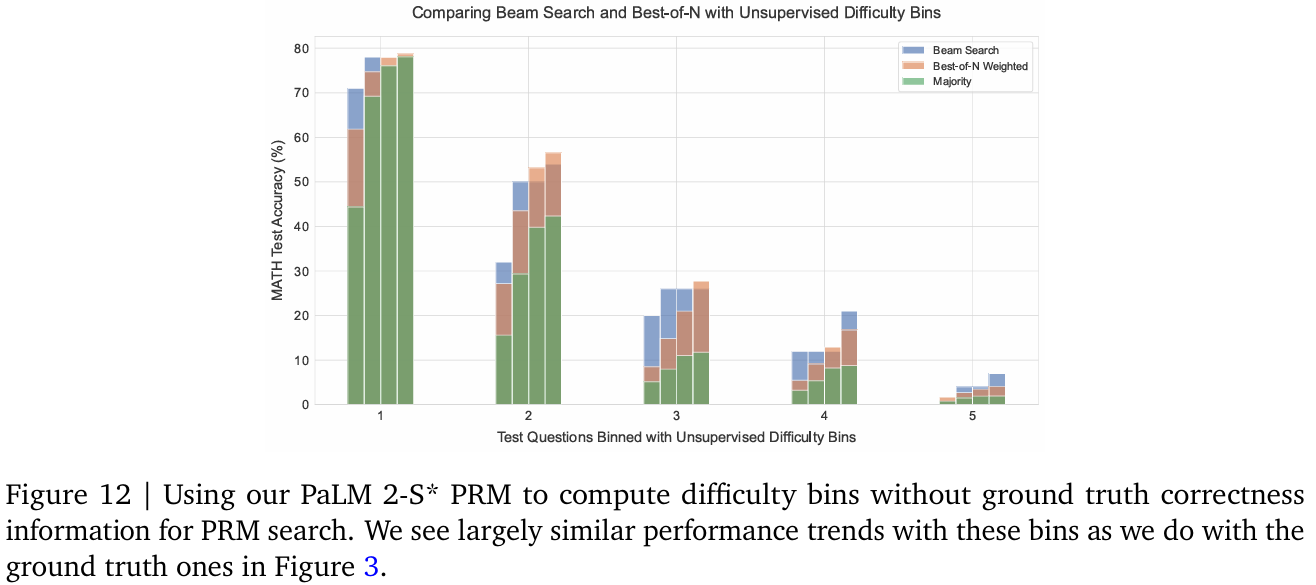
圖12和圖11分別展示了使用預測難度分箱的PRM搜索與修正結果。兩種設置下,預測難度分箱均呈現與真實難度分箱類似的趨勢。
D. PRM訓練細節
我們將PRM微調為二分類器,預測解決方案每一步的0-1值。模型通過蒙特卡洛展開獲得的軟標簽訓練,使用二分類交叉熵損失函數(例如?(ylog?(y^)+(1?y)log?(1?y^))-(y\log(\hat{y})+(1-y)\log(1-\hat{y}))?(ylog(y^?)+(1?y)log(1?y^?))),其中yyy為軟真實值,y^\hat{y}y^?為模型預測值。使用AdamW優化器微調基礎模型,參數為:學習率3e?53\mathrm{e-}53e?5,批大小128,丟棄率0.05,Adam參數(0.9,0.95)(0.9,0.95)(0.9,0.95)。通過早停選擇驗證損失最低的 checkpoint,驗證集為PRM80Ok訓練集的10%隨機樣本。
PRM在每個問題的少樣本提示基礎模型上微調,每問題采樣16個樣本。每步使用16次蒙特卡洛展開(基于相同基礎模型和提示)估計步級價值。過濾掉所有無法輸出有效可解析最終答案的樣本,因初始實驗發現此類樣本損害PRM性能。
圖11和圖12分別展示了使用PaLM 2-S* PRM計算無真實答案難度分箱的修正與PRM搜索結果,趨勢與真實難度分箱(圖7和圖3)一致。
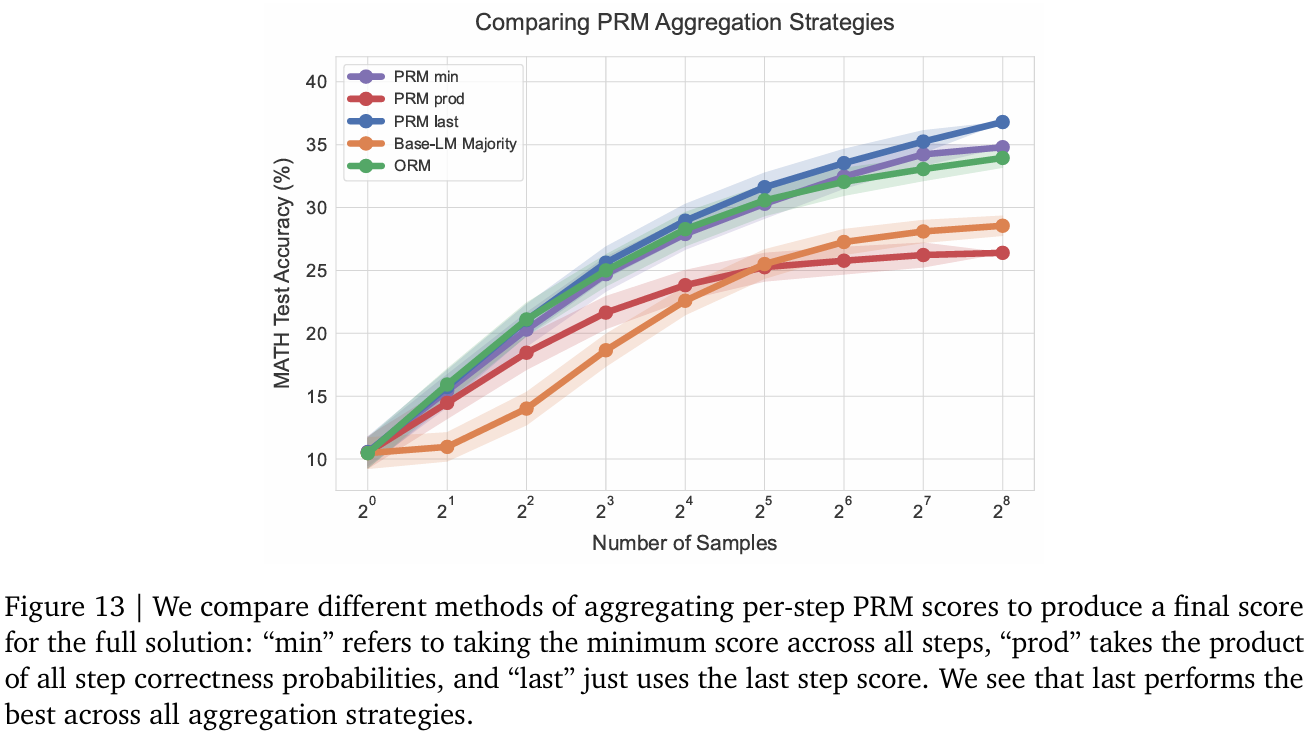
E. PRM聚合策略對比
我們對比了不同聚合步級PRM評分以生成最終解決方案評分的方法:1)取所有步的最小分(Lightman等人[22]方法,即“min”);2)取所有步正確概率的乘積(即“prod”);3)僅取最后一步預測(即“last”)。圖13顯示,最后一步預測在所有聚合策略中表現最佳。此前研究[22,45]發現“min”最優,但我們認為差異源于我們的驗證器基于軟蒙特卡洛回報標簽訓練,與二進制正確性標簽表面差異顯著,故其他聚合策略效果不同。
有趣的是,使用最后一步聚合時,PRM實質上被用作ORM。但PRM性能優于ORM,表明我們的步級PRM訓練更多是表征學習,而非純推理工具。未來研究應進一步探索此方向。
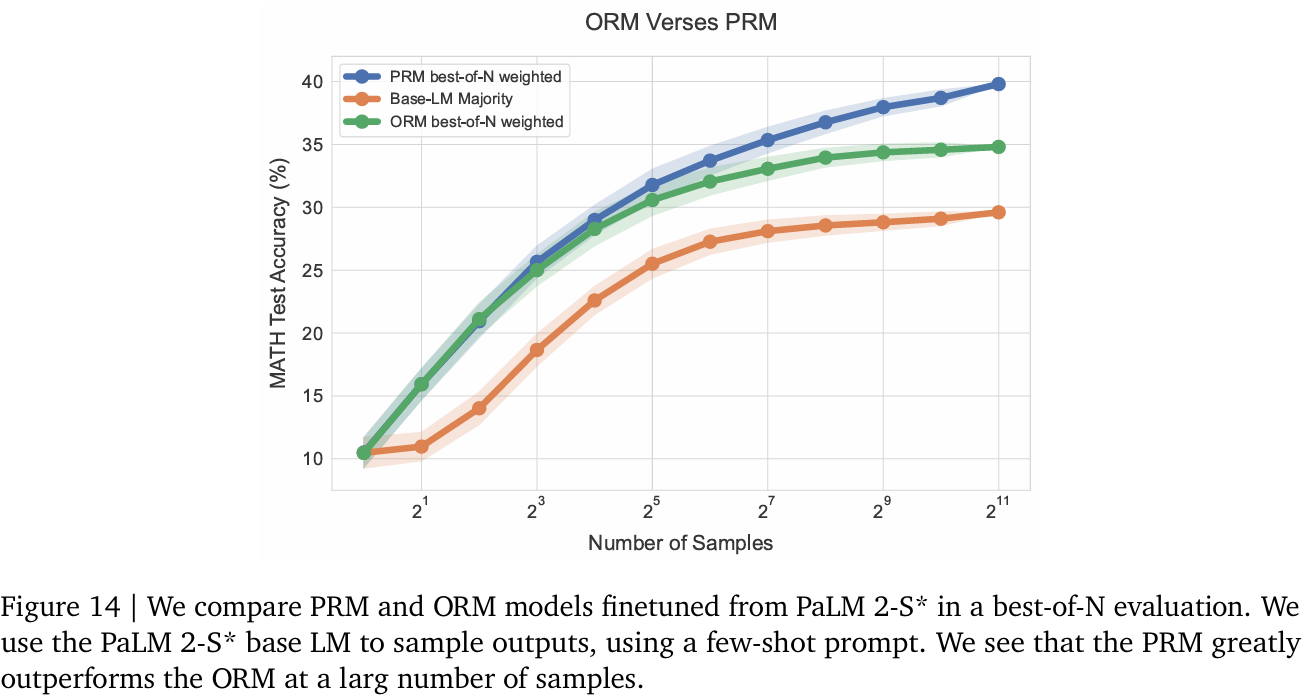
F. PRM與ORM對比
我們使用PaLM 2-S*基礎LM訓練了PRM和ORM模型。圖14顯示,PRM性能顯著優于ORM,且差距隨樣本量增加而擴大。PRM使用最后一步預測評分答案(如附錄E所述)。
G. 提示細節
為使基礎模型輸出可應用PRM的逐步格式答案,我們采用4樣本提示,樣本選自Lightman等人[22]發布的PRM800k數據。具體使用第1階段訓練集的GPT-4生成正確答案示例,包含正確逐步格式。初始實驗發現此提示與Lewkowycz等人[20]的提示效果相似。該提示用于生成PRM和修正模型的訓練數據,也在測試集上用于PRM搜索。最終答案評分采用Lightman等人[22]發布的評分函數。
H. 修正模型微調細節
修正模型的微調流程遵循第6.1節所述方法。我們首先為每個問題采樣64個輸出,并過濾掉所有以無效解結尾的答案。對于每個正確答案,我們統一隨機采樣0到4之間的整數,指示在訓練軌跡中包含多少個錯誤答案作為上下文。正確答案作為軌跡的最后一個答案(模型被訓練生成該答案),錯誤答案被包含在上下文中。若采樣數大于0,我們根據字符級編輯距離指標選擇最接近的錯誤答案作為軌跡的最后一個錯誤答案,目標是選擇與正確答案有一定關聯的錯誤答案以提升學習效果。剩余錯誤答案從可用答案中隨機采樣。若采樣到的錯誤答案不足4個,我們將均勻分布的最大值調整為實際錯誤樣本數。我們使用此流程為訓練集中的所有問題生成軌跡,并基于這些軌跡中的正確答案微調基礎語言模型。優化器采用AdamW,參數為:學習率1e?51\mathrm{e}{-5}1e?5,批大小128,丟棄率0.0,Adam參數(0.9,0.95)(0.9,0.95)(0.9,0.95)。
我們發現,基于上述流程生成的驗證集評估損失并不適合作為早停信號。實際上,在驗證損失開始上升后的檢查點往往具備更強的修正能力。這可能是因為微調后的修正模型生成的軌跡屬于策略外數據,自然與模型自身策略內生成的軌跡分布不同。因此,我們選擇在驗證集過擬合后稍晚的檢查點作為修正模型。
I. 修正模型選擇準則
如第6.1節所述,為有效使用修正模型,需部署兩類選擇標準:1)ORM驗證器;2)多數投票。
對于ORM驗證器,我們根據附錄J的流程在修正模型輸出上訓練ORM。推理時,使用該驗證器選擇最佳答案。由于存在兩類聚合維度(修正軌跡內部和軌跡之間),我們采用分層策略:首先在每條修正軌跡內通過最佳N加權聚合選擇最高分答案,然后在所有軌跡的選中答案中再次進行最佳N加權聚合,最終輸出作為最終預測。
對于多數投票,我們發現分層聚合在軌跡數或長度較小時存在問題(樣本不足導致多數投票失效)。因此,多數投票直接聚合所有軌跡的所有答案,取多數作為最終答案。此方法在擴展性上表現更穩定。
J. 修正模型驗證器訓練
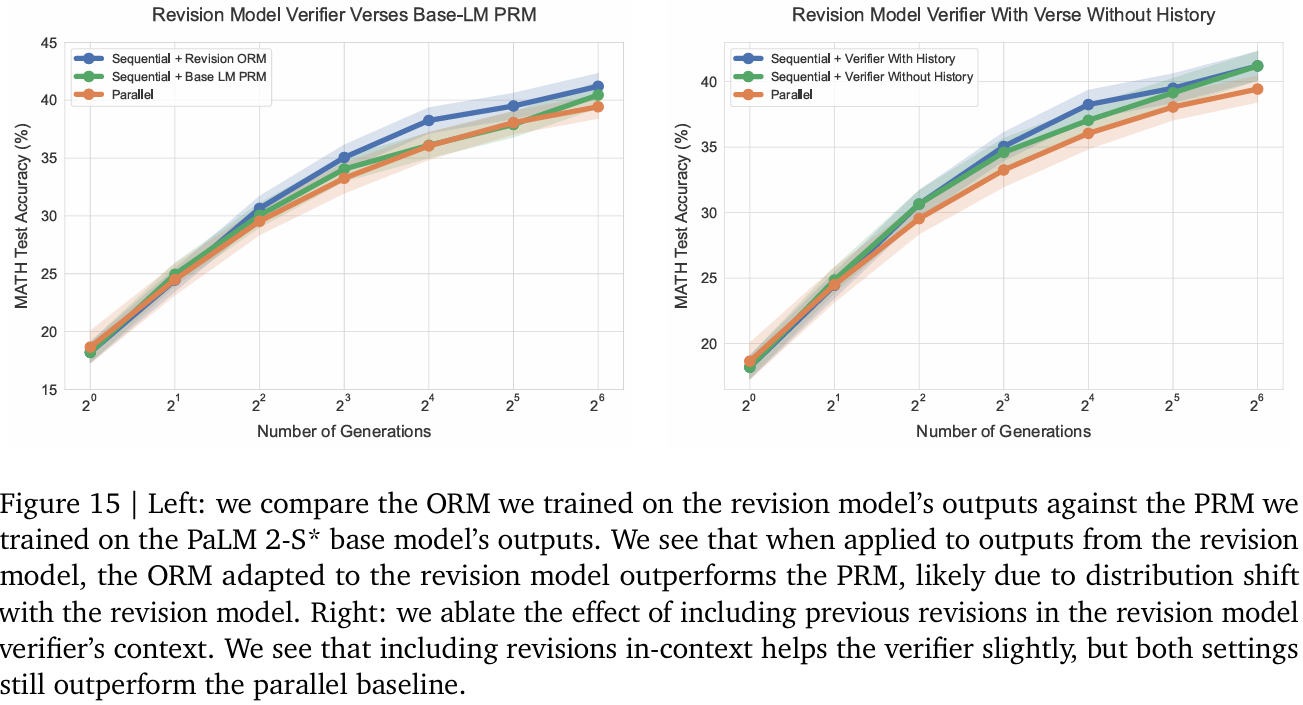
我們發現,在PaLM 2-S修正模型輸出上訓練的PRM效果不佳(見圖15(a)),可能是由于修正模型導致的分布偏移。因此,我們為PaLM 2-S修正模型單獨訓練ORM驗證器(未選擇PRM因生成步級標簽成本過高)。
針對修正場景,我們略微調整標準ORM:在微調時將歷史修正步驟作為上下文輸入,使驗證器與修正模型共享相同上下文,從而在評分時能參考歷史嘗試。其余實驗細節與PRM訓練一致。
實證表明,包含歷史修正的上下文能略微提升驗證器性能(見圖15(b))。即使不包含歷史修正,順序修正仍略優于并行采樣,說明順序采樣的提升不僅源于驗證器上下文。
K. ReST EM修正模型實驗
我們嘗試用簡化RL算法ReST EM[35]進一步優化PaLM 2-S*修正模型。具體而言,在MATH訓練集上為每個問題生成最多5步的64條修正軌跡,并在軌跡中首次出現正確答案時停止。基于此數據微調基礎LM。為幫助模型學習任務,我們顯式平衡了軌跡長度的分布。
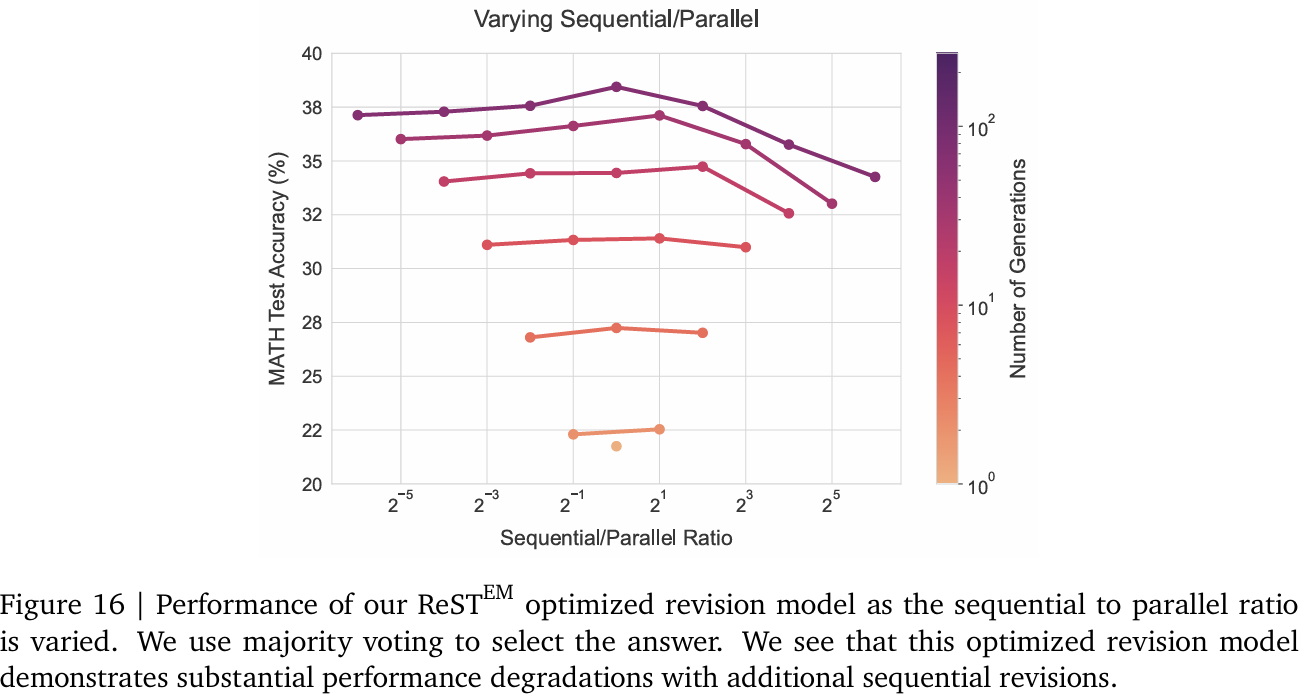
圖16展示了新修正模型隨順次-并行比例變化的性能。可見,額外順次修正對此模型性能損害顯著。我們推測,因ReST EM在線數據采集加劇了修正數據中的虛假關聯,導致優化后的模型無法有效學習修正任務。我們認為,采用Qu等人[28]的離線數據收集策略可能更有效,留待未來研究。
L. 修正模型輸出示例
圖17-23展示了修正模型的多個輸出示例。







M. PRM束搜索輸出示例
圖24-29展示了PRM束搜索的多個輸出示例,包含每步的PRM評分(0到1之間)。







![Rust 項目編譯故障排查:從 ‘onnxruntime‘ 鏈接失敗到 ‘#![feature]‘ 工具鏈不兼容錯誤](http://pic.xiahunao.cn/Rust 項目編譯故障排查:從 ‘onnxruntime‘ 鏈接失敗到 ‘#![feature]‘ 工具鏈不兼容錯誤)

)





)






