preface

雖然我知道專業課必須得學，但是要學的東西，好多，我對專業課很害怕，稍微往后挪一挪，今天學了兩個強化網課之后再學專業課吧。今天的目標是學完 11 到 14.任重道遠，加油！從今天開始盡量早睡，感覺晚睡對自己身體不好。

intensify 79

這題就是算一個導數，一元隱函數求導，算極值，首先找可疑點，可疑點就是駐點和不可導點，這題沒有不可導點，就找駐點，用第二充分條件就好。實際上一元隱函數我們非常喜歡求一階導，二階導，然后算出來之后就是最后的答案了。

intensify 80

復習完這一節內容去睡覺。感覺想要學好知識點，就得多睡覺。腦力勞動者必須多睡覺。駐點就是一階導數為零的點。判斷駐點用導數定義就行，判斷去心鄰域的單調性，用去心鄰域的導數極限，然后發現是振蕩的，所以不單調。判斷極值有四個方法，定義，第一充分條件，二和三。畫圖有五個注意點，定義域和奇偶性，單調性，凹凸性，特殊點，漸近線。左右開弓有五種情況，指數，反正切，絕對值，分段，取整。抽象函數極限有兩種方法，洛必達湊導數定義，泰勒。分段函數求導有兩種方法，分段點外直接求分段點上導數定義，或者導數極限定理。導數極限定理有三個條件，原來函數在某點連續，去心鄰域內可導，去心鄰域的導數的極限是不振蕩的。算了，先去睡覺，磨刀不誤砍柴工。

intensify 81

這題有兩個方法。method 1: 舉例法，特別快。首先對給的極限做一下等價變形，然后得到 $\underset{x\to 2}{\lim }\frac{f(x)}{(x?2{)}^2}=\frac{3}{2}$，我們可以讓 $f(x)=\frac{3}{2}(x?2{)}^2$ ，然后算出來導數，然后繪圖用定義法判斷極值，排除三個錯誤選項，選出正確選項。舉例排除法只能否定，也就是說，舉例排除法只能做選擇題。

method 2: 使勁分析。湊導數定義，這塊兒實際上是抽象函數極限，要么洛必達湊導數定義，要么泰勒，這塊實際上不好泰勒，因為鄰域內可導沒有這個條件，洛必達也只是可以到連續的那階，所以本質就是只有一個方法，湊導數定義。然后算極值，只有四個方法，定義（鄰域內的最值），第一、二、三充分條件。這題只能用定義，因為鄰域內一階可導性未知，不能第一充分條件，不知道二階導數，不能第二充分條件，同理，不能第三充分條件。最后有一個關鍵點，就是用定義來分析，要利用函數極限的去帽保號性，就是把極限符號去掉，在去心鄰域內，函數的值是正的，假設原來極限的值是正的。然后一頓分析就可以了。

intensify 27 preserve

說到保號性，寫一道保號性的題練習一下叭。這題沒有任何難度，當自變量充分大的時候，就是指數函數大于冪函數大于對數函數。極限是這樣，去心鄰域也是這樣。x 充分大就是 $x\to +\infty$

保號性這塊我感覺自己沒有學得非常扎實，就返回去看之前講這個知識點的視頻，這就是有效的復習！

basics 1.11

純概念題，考試的時候不會價值五分，但是可以作為一個很細的點來幫助理解概念。極限存在，函數在去心鄰域內處處有定義。極限存在，函數在去心鄰域內處處有定義。極限存在，函數在去心鄰域內處處有定義。極限存在，函數在去心鄰域內處處有定義。極限存在，函數在去心鄰域內處處有定義。極限存在，函數在去心鄰域內處處有定義。

basics 1.12

求極限之后用去帽保號性，非常簡單。

basics 1.13

這題太牛了。

basics 1.10

絕對的好題。絕對值不等式 $||a|?|b||\le ||a|\pm |b||\le |a|+|b|$ 。還有一些基本的不等式子。也要積累一下。$x>0,\frac{1}{x+1}<\ln (1+\frac{1}{x})<\frac{1}{x}$ 。很多知識點，實際上也沒有那么難記，實在不行多抄幾遍就可以記住了。用 $??\delta$ 語言描述極限的定義即可。

basics 1.62

這題主要是考察，假設兩個數列的極限相等，那么去心鄰域內是無法比較大小的。函數極限存在，那么函數去心鄰域內處處有定義。12 點睡覺吧，太早了睡不著覺。

basics 1.14

加帽保號性需要加上等號。加帽保號性需要加上等號。加帽保號性需要加上等號。最重要的就是真題卷。到時候好好刷一刷真題卷子。反復刷就能提升。因為反復刷一定可以吃透，吃透之后就可以有希望沖擊一個高分。

intensify 82

微分方程和最大值結合的一個題，23 年的真題，我來判斷一下自己還是否熟練這個題。運算量還算可以，可能要算個幾分鐘，沒啥思維量，第一問這種操作有點秀，他媽的給一個動點作為切點，我直接翻車了，第一問做出來之后，后面的基本就是送分的。

basics 2.48

這塊構造非常巧妙，到時候還會有一本沖刺講義。我感覺數學多刷經典題真的穩了。所以加油。現在關鍵就是把強化題刷穿，強化題刷穿之后，沖刺，真題，模擬卷，就可以了。模擬卷。。。

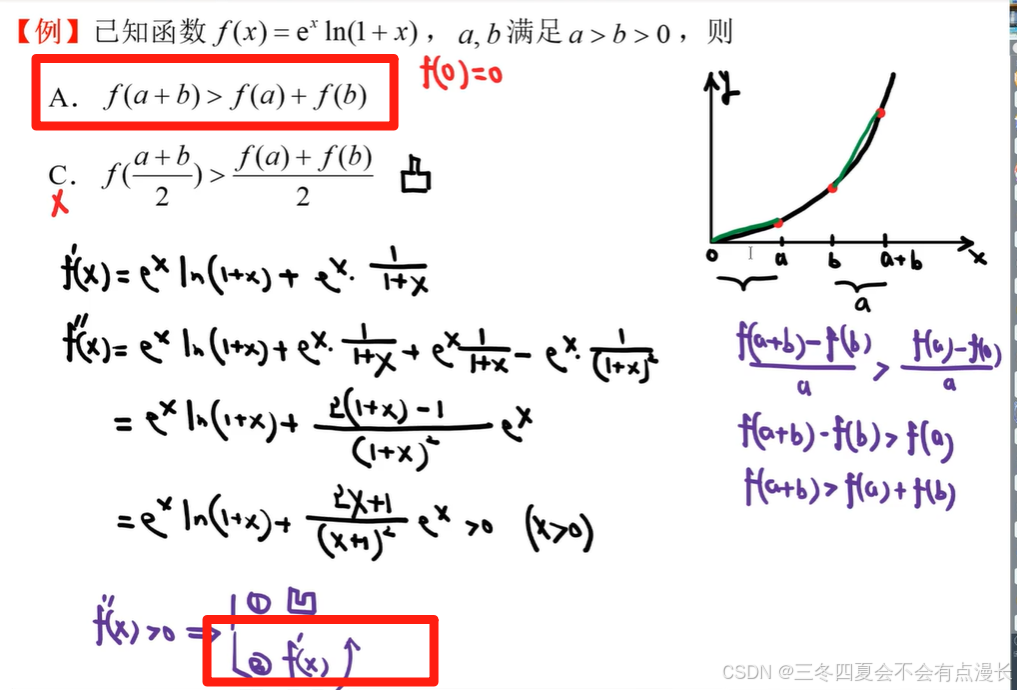
可惡，不想分小標題了。有點累了。慢慢來，這種題很難想到其實。就是考慮一階導數的增長對于斜率增長速度的影響，當然知道解析了肯定能看懂，但是自己獨立考慮真的能想出來嗎。之后可以考慮把幾個特殊的點的數值代進去先寫在草稿紙上面。做數學題一定要慢一點。可以考慮移項構造不等式，尤其是考慮 0 1 -1 這種特殊的點，還有一階導數單調遞增表現在原來函數的圖象里面就是斜率越來越大，圖象越來越陡峭。

84：這題稍微比較簡單，把給的式子化簡，注意到是一條直線，并且過 ( 0, f ( 0 ) ), 斜率是兩點割線的斜率，然后知道單增難以知道凹凸性，知道凹凸性，就考慮單增和單減，發現都是第三個選項的答案。總結來說，核心就是知道凹凸性的三種定義，中點，割線和切線。嘴上說著過去了，心里偷偷折了個角。折個角的意思就是要多多復習回顧呢。早點睡覺好一點，這樣對身體好一點。slowness leads to stability, and stability leads to speed.

83: 這題差點忘記做了。我發現我很容易被一些事情干擾，然后轉頭去做和學習無關的事情，這樣讓我的學習效率稍微有點低了。還是得提升自己的專注力。一階導數在某點大于零，不能推出原來函數該點去心鄰域單調遞增，除非告訴了一階導數在該點連續。單調遞增，導數大于等于零。凹函數，二階導數大于等于零。二階導數大于零，不能推出原來函數在該點的鄰域是凹的，除非告訴二階導數在該點連續。總結就是要鄰域就要連續。并且是高階的連續。一點連續不能推出鄰域連續。一點可導不能推出鄰域可導。一點導數大于零，不能推出鄰域單調遞增。一點二階導數大于零，不能推出鄰域凹函數。都缺失了一些條件。

指數函數作為一個乘法因子求導，反正指數 $e^x$ 都是一致的，所以就是剩下的因子求導，不求導，然后加起來。比如說，$(x{e}^x{)}^{\prime }=e^x(x+1)$，再比如說$(x^2+a)e^x=e^x(x^2+a+2x)$ ，感覺這種總結老師一般都不會總結，這種小的 trick 自己好好總結一下就好了。屬于是真正提升自己水平的 trick .

85 這題實際上考了一個簡單的概念，也是真題，有點厲害哈哈哈。雖然不難。我考慮一下，數學有 4 個高數的選擇題，3 個高數的填空題。433 411，86 + 32 + 32 = 150， 所以數學肯定是高數是最重要的板塊。也就是說高數 8 個小題，線代 4 個小題，概率 4 個小題，80 分小題，高數 4 個大題，46 分，線代概率各一個大題，24，小題 80 分，大題 70 分，所以說，實際上是得小題者得天下。要是小題可以拿一個很高的分數，那么考研數學基本上穩了。

86 這個題比較簡單，就是算導數，然后考極值和拐點的充分條件，第三充分條件，前面的導數都是相等的，并且都等于零，最后算出來一個 n 階導數，假設這個 n 是偶數，表示這個可能是極值點，這個 n 階導數是正的，極小值，負的，極大值，奧，也只有這兩種可能，不可能等于零，我說了這一階的導數不是零。假設是奇數，表示這個點不是極值點。

假設最后算出來這個階數是偶數，表示這個點不是拐點。假設算出來階數是奇數，表示這個點是拐點。拐點實際上一般都不是極值點我感覺。我這個問題有點含金量呀，極值對應的坐標是否和拐點一定不是同一個點？假設可導的話，一定不是同一個點。假設不可導的話，有可能是同一個點。極值需要連續，然后可疑點是一階導數為零或者一階導數不存在。

我們這里首先考慮可導的情況吧。可導的話，考慮極小值，一階導數為零，二階導數為零，假設 $x_0$ 左側的一階導數是負的，二階導數是負的，右側都是正的。那么畫出原來函數和一階導數的圖象，都是先減小后增大，然后一階導數在左邊是負的，減小肯定是更小，換句話說更負，不可能到 $x_0$ 的時候變成 0，因為 0 大于任何負數。所以得到矛盾了，所以可導的時候，極值點對應的坐標和拐點一定不是同一個點。

假設一階導數不存在，二階導數不存在，有可能出現重合。

我以為自己發現新大陸了，結果張宇書上面總結好了都。哈哈哈。所以的話，也沒啥，吃透一個老師的核心資料就足夠了。題目是做不完的，結論也是記不完的，把核心的東西搞熟練就可以了。

感覺這樣總結挺沒勁的，還是不這樣總結了。還是自己書上隨便寫點兒，太慢了，我很著急，火燒眉毛，燃眉之急了。。。調整調整吧。何時葡萄先熟透，你要靜候再靜候。