機器學習通關秘籍｜Day 03：決策樹、隨機森林與線性回歸

一、決策樹

1、概念

2、基于信息增益的決策樹的建立

（1）信息熵

（2）信息增益

（3）信息增益決策樹建立步驟

3、基于基尼指數的決策樹的建立

4、API

二、隨機森林

1、算法原理

2、API

三、線性回歸

1、回歸

2、線性回歸

3、損失函數

4、多參數回歸

5、最小二乘法

6、API

四、總結

一、決策樹

1、概念

????????決策樹是一種常用的機器學習算法，用于解決 分類和回歸問題。它通過遞歸地將數據集劃分為子集，構建一棵樹形結構，每個節點代表一個特征或屬性的判斷條件，葉子節點表示最終的分類結果。

2、基于信息增益的決策樹的建立

????????決策樹的核心思想是通過選擇最優的特征進行劃分，從而減少數據的不確定性。以下是基于信息增益的決策樹建立步驟：

（1）信息熵

信息熵描述的是 不確定性。信息熵越大，不確定性越大。信息熵的值越小，則X的純度越高。

信息熵是衡量數據集純度的一個指標，公式如下：

示例：假設一個數據集中有 10 個樣本，其中 6 個屬于類別 A，4 個屬于類別 B，則信息熵為：

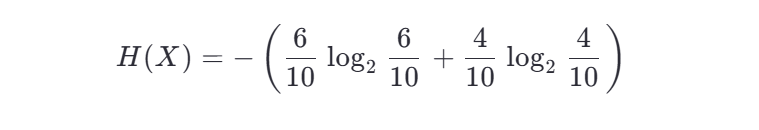
（2）信息增益

????????信息增益（Information Gain）是決策樹中用于選擇最優分裂特征的核心指標。它的基本思想是：選擇能夠最大程度降低數據不確定性的特征進行劃分。不確定性由信息熵衡量，信息增益越大，說明使用該特征劃分后，數據變得更“純凈”，分類效果更好。???????

?????????信息增益是一個統計量，用來描述一個屬性區分數據樣本的能力。信息增益越大，那么決策樹就會越簡潔。這里信息增益的程度用信息熵的變化程度來衡量, 信息增益公式： ? ? ? ? ??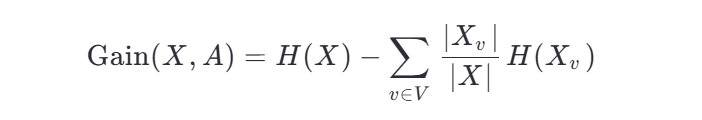

（3）信息增益決策樹建立步驟

????????下面我們通過一個具體例子來詳細計算信息增益：

假設我們有一個數據集共 10 個樣本，目標是預測用戶是否會購買某產品（類別 A：購買，類別 B：不購買）。我們考慮使用“天氣”這一特征進行劃分，其分布如下：

天氣	樣本數	購買	不購買
晴天	6	5	1
雨天	4	1	3
總計	10	6	4

我們的目標是計算使用“天氣”作為分裂特征時的信息增益。

第一步：計算原始數據集的信息熵 H(X)

原始數據集中：

信息熵為：

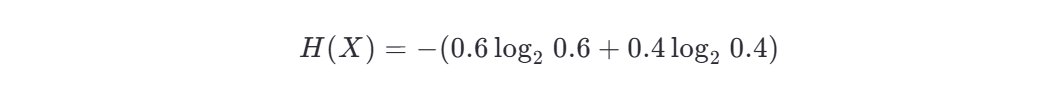
計算對數值（可使用計算器）：

代入：

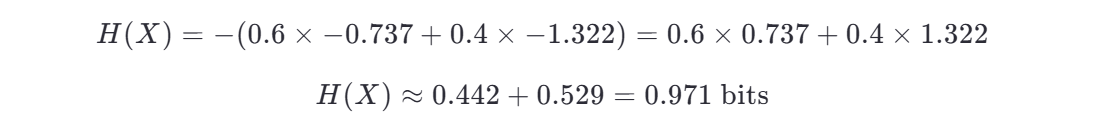
第二步：計算每個子集的信息熵 H(Xv?)

(a) 晴天子集（6 個樣本）

(b) 雨天子集（4 個樣本）

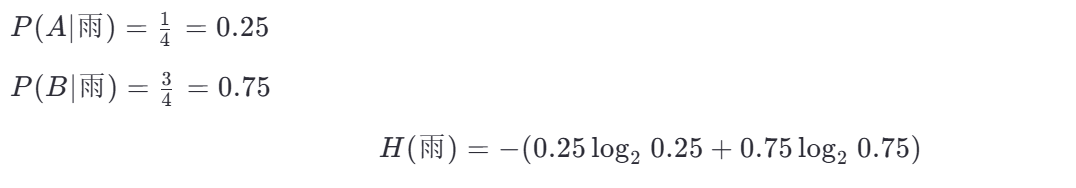
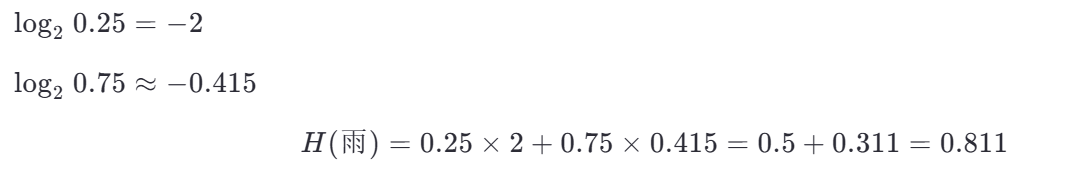
第三步：計算加權平均熵

第四步：計算信息增益

信息增益與決策判斷的關系

信息增益越大，說明該特征對分類的幫助越大。在這個例子中，“天氣”帶來了 0.256 的信息增益，意味著通過“天氣”劃分后，整體數據的不確定性顯著下降。
在構建決策樹時，我們會比較所有特征的信息增益，選擇增益最大的特征作為當前節點的分裂依據。
例如，如果另一個特征“溫度”的信息增益是 0.32，大于“天氣”的 0.256，那么我們就會優先選擇“溫度”進行分裂。
這體現了決策樹的貪心策略：每一步都選擇當前最優的特征，逐步構建一棵高效的分類樹。

3、基于基尼指數的決策樹的建立

基尼指數是另一種衡量數據集純度的指標，公式如下：

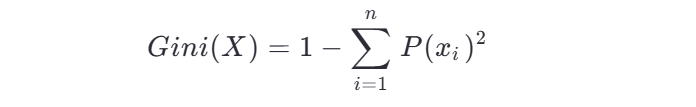
基尼指數越小，數據集的純度越高。

4、API

代碼示例：

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.model_selection import train_test_split
x, y = load_iris(return_X_y=True)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0)
# 創建決策樹模型
model = DecisionTreeClassifier()
model.fit(x_train, y_train)
print(model.score(x_test, y_test))y_pred = model.predict([[4.3, 2.6, 1.5, 1.3]])
print(y_pred)
# 導出已經構建的據冊數
export_graphviz(model, out_file='../src/tree.txt', feature_names=['花萼長度', '花萼寬度', '花瓣長度', '花瓣寬度'])

結果展示：

二、隨機森林

? ? ? ? 森林，顧名思義，就是有很多棵樹。

1、算法原理

????????隨機森林是一種基于決策樹的集成學習方法，通過構建多棵決策樹并結合它們的預測結果來提高模型的泛化能力。其核心思想包括：

Bootstrap 抽樣：從原始數據集中有放回地抽取多個子集，每棵樹使用不同的子集進行訓練。
隨機特征選擇：在每個節點分裂時，只考慮一部分隨機選擇的特征，而不是全部特征。
投票機制：對于分類任務，最終預測結果是所有樹的多數投票結果；對于回歸任務，最終預測結果是所有樹的平均值。

2、API

RandomForestClassifier ( n_estimators=100,? max_depth=5,? criterion='entropy' )

n_estimators: 樹的數量,????????????????

max_depth: 樹的最大深度,

criterion: 評價標準(entropy: 熵, gini: 基尼系數)

代碼示例：

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
# 加載數據集
x, y = load_iris(return_X_y=True)
# 數據集劃分
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0)
# 標準化
scaler = StandardScaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)
# 創建隨機森林模型 n_estimators: 樹的數量, max_depth: 樹的最大深度, criterion: 評價標準(entropy: 熵, gini: 基尼系數)
model = RandomForestClassifier(n_estimators=100, max_depth=5, criterion='entropy')
model.fit(x_train, y_train)
score = model.score(x_test, y_test)
print(score)
# 預測新數據
y = model.predict([[1.3,2.5,1.1,0.5]])
print(y)

結果展示：

三、線性回歸

1、回歸

????????回歸的目的是預測數值型的目標值y。最直接的辦法是依據輸入x寫出一個目標值y的計算公式。假如你想預測某人的體重（因變量），根據他的身高（自變量）。通過收集一些人的身高和體重數據，我們可以找到它們之間的關系。

張三的體重? ? =? ? 0.86? ? *? ? 張三的身高? ? -? ? ? 0.5? ? ?*? ? ? ?張三的運動時間

這就是所謂的回歸方程（regression equation），其中的? 0.86 和 0.5? 稱為回歸系數（regression weights），求這些回歸系數的過程就是回歸。一旦有了這些回歸系數，再給定輸入，做預測就非常容易了。具體的做法是用回歸系數乘以輸入值，再將結果全部加在一起，就得到了預測值。

2、線性回歸

概念：線性回歸是回歸的一種，它假設因變量與自變量之間存在線性關系。也就是說，可以用一條直線來近似描述它們的關系。
例子：如果身高和體重的關系是線性的，那么我們可以畫一條直線，這條直線可以表示為：

其中，“斜率”表示身高每增加1單位，體重平均增加多少；“截距”表示當身高為0時的體重值（雖然實際中身高不可能為0，但這是數學上的起點）。

3、損失函數

（1）線性方程

? ? ? ? 我們為了讓我們得到的 方程（模型）更加地貼近真實值，盡可能地提高準確率，由此提出了損失函數。

我們假設這個最優的方程是:

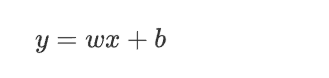
這樣的直線隨著w和b的取值不同可以畫出無數條

（2）為了求解最優值，我們引入損失函數

在這無數條中,哪一條是比較好的呢?

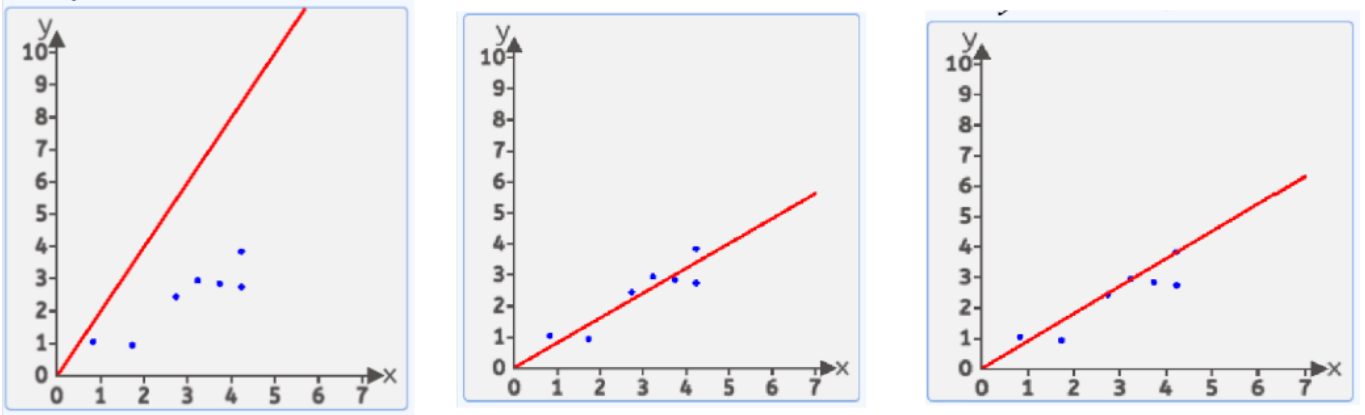
我們有很多方式認為某條直線是最優的,其中一種方式:均方差

就是每個點到線的豎直方向的距離平方求和在平均最小時這條直接就是最優直線

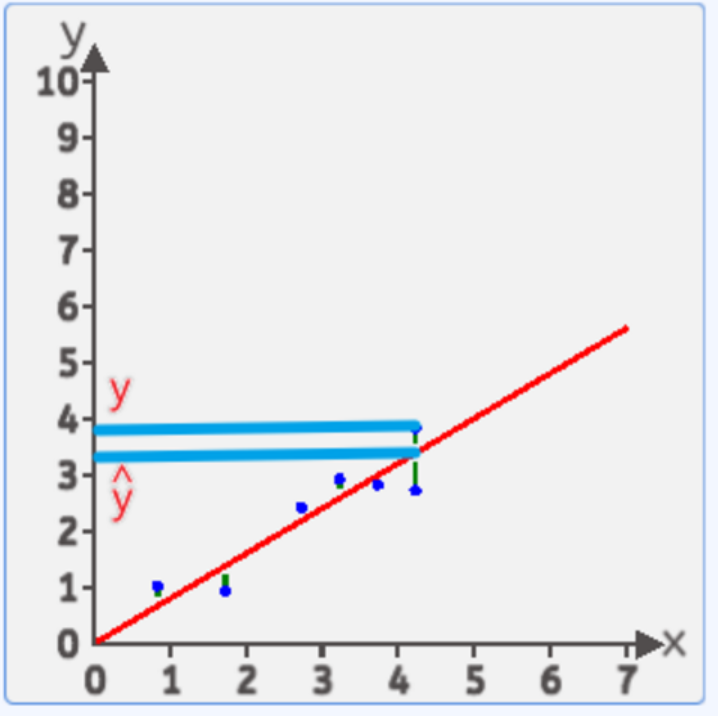
????????可能很多讀者會疑惑一個問題：為什么我們要取豎直方向上的差值？而不是對于這一點向直線做垂線求距離呢？

????????我們只需要搞清楚，直線上的點代表著 預測值 ，而樣本點的 y 值代表了真實值，所以豎直距離上的差值，就是誤差

然后計算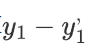表示第一個點的真實值和計算值的差值 ,然后把第二個點,第三個點...最后一個點的差值全部算出來

有的點在上面有點在下面,如果直接相加有負數和正數會抵消,體現不出來總誤差,平方后就不會有這個問題了

所以最后:

總誤差(也就是傳說中的? 損失? ):

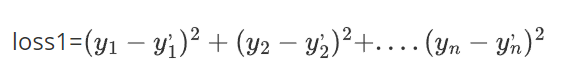
平均誤差(總誤差會受到樣本點的個數的影響，樣本點越多，該值就越大，所以我們可以對其平均化，求得平均值，這樣就能解決樣本點個數不同帶來的影響)

這樣就得到了傳說中的損失函數:

（此處的 x值任取，只是舉個例子）

怎么樣讓這個損失函數的值最小呢?

（3）利用初中拋物線的知識或者高中的求導知識求得最低點

我們先假設b=0

然后就簡單了，算 w 在什么情況下損失函數的值最小(?初中的拋物線求頂點?的橫坐標,?高中求導數為0時)

求得w=0.795時損失函數取得最小值

那我們最終那個真理函數(最優解)就得到了

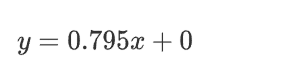
注意：

實際數據中 x 和 y 組成的點不一定是全部落在一條直線上
我們假設有這么一條直線 y=wx+b 是最符合描述這些點的
最符合的條件就是這個方程帶入所有x計算出的所有y與真實的y值做 均方差計算
找到均方差最小的那個w
這樣就求出了最優解的函數(前提條件是假設b=0)

4、多參數回歸

概念：多參數回歸是指自變量不止一個的情況。例如，除了身高外，還可能考慮年齡、性別等因素來預測體重。
例子：如果我們不僅用身高預測體重，還加入年齡作為另一個自變量，那么線性回歸的公式就變成了：

這里有兩個斜率，分別表示身高和年齡對體重的影響。

5、最小二乘法

概念：最小二乘法是一種優化方法，用于求解線性回歸中的參數（如斜率和截距），使得損失函數（通常是均方誤差）最小化。
目標：找到一組參數，使得損失函數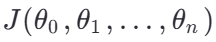最小。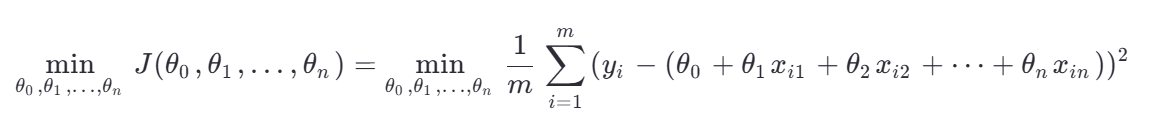
求解方法：可以通過解析法（如正規方程）或數值優化方法（如梯度下降）來求解最小化問題。
- 正規方程（適用于小規模數據）：
  
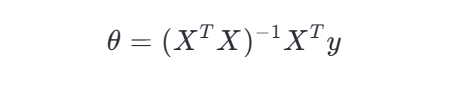
  其中：
- 梯度下降（適用于大規模數據）：
  
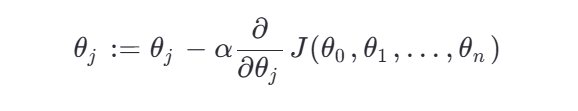
  其中：
例子：假設我們有幾組身高和體重的數據，最小二乘法會調整直線的位置（即調整斜率和截距），使得所有數據點到直線的距離平方和最小。這樣得到的直線就是最佳擬合直線。

6、API

代碼示例：

from sklearn.linear_model import LinearRegression
import numpy as np
# 創建具有8個特征和1個目標值的數據集
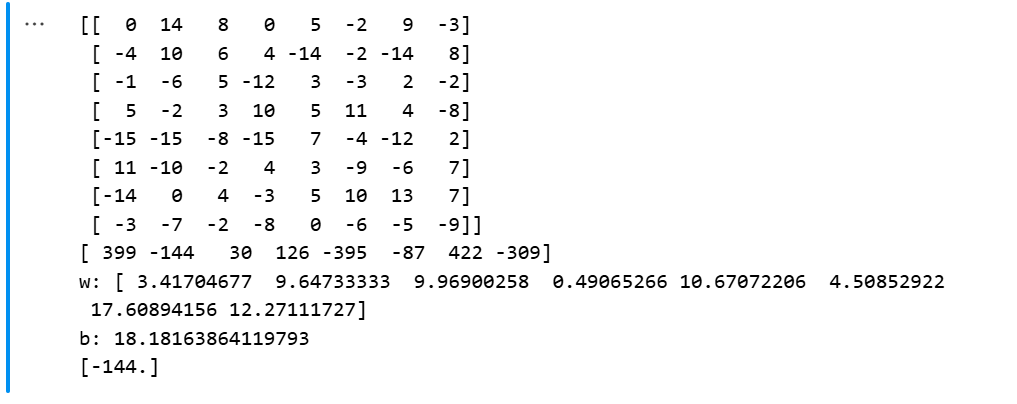
data=np.array([[0,14,8,0,5,-2,9,-3,399],[-4,10,6,4,-14,-2,-14,8,-144],[-1,-6,5,-12,3,-3,2,-2,30],[5,-2,3,10,5,11,4,-8,126],[-15,-15,-8,-15,7,-4,-12,2,-395],[11,-10,-2,4,3,-9,-6,7,-87],[-14,0,4,-3,5,10,13,7,422],[-3,-7,-2,-8,0,-6,-5,-9,-309]])
# 取全部行，除了最后一列的全部列，也就是八個特征
x = data[:, :-1]
# 取全部行，最后一列，也就是目標值
y = data[:, -1]
print(x)
print(y)
# 創建線性回歸模型
model = LinearRegression()
# 訓練
model.fit(x, y)
# 權重
print("w:",model.coef_)
# 偏置
print("b:", model.intercept_)
# 預測新數據
y_pred = model.predict([[-4,10,6,4,-14,-2,-14,8]])
print(y_pred)

結果展示：

四、總結

決策樹 是一種基于樹形結構的分類和回歸算法，通過信息增益或基尼指數進行特征選擇。

隨機森林 是基于決策樹的集成學習方法，通過 Bootstrap 抽樣和隨機特征選擇提高模型的泛化能力。

線性回歸 是一種簡單的回歸模型，通過最小二乘法或梯度下降等方法求解權重參數。

希望這篇博客對你有所幫助！如果有任何問題，歡迎進一步討論。