題目

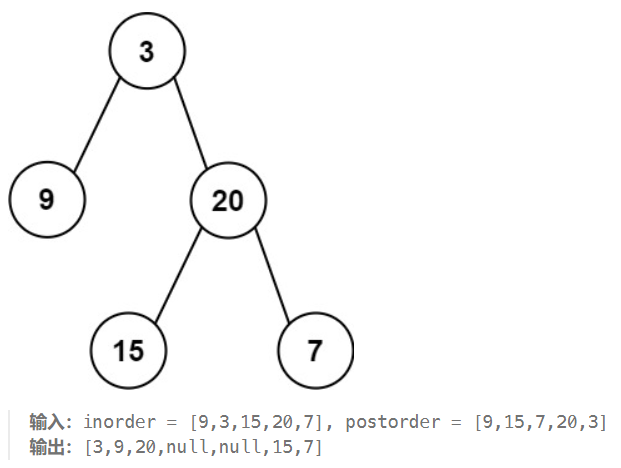
給定兩個整數數組 inorder 和 postorder ，其中 inorder 是二叉樹的中序遍歷， postorder 是同一棵樹的后序遍歷，請你構造并返回這顆 二叉樹 。

思路

我們首先要知道中序遍歷和后序遍歷分別都是什么。
中序遍歷是依照左子樹，根節點，右子樹的順序來進行遍歷。
后序遍歷是依照左子樹，右子樹，根節點的順序來進行遍歷。
我們觀察這兩個遍歷得到的數組看能得到什么信息，首先最明顯的是我們通過后序遍歷可以確定整個二叉樹的根節點也就是后序數組的最后一個位置除此之外也沒啥了，接下來是中序數組，中序數組乍一看沒啥信息可言但是我們來看其中根節點的位置，再看它的左邊和右邊我們可以發現整個數組我們只要確定了根節點的位置就可以劃分成三部分：左子樹，根節點和右子樹。那么再找到左子樹和右子樹的根節點不就可以繼續劃分下去了嗎直到根節點是一個葉子節點沒有左子樹和右子樹。這不就是分治的思想嗎，先進行拆分再進行組合。所以這道題我們可以使用分治來做，從根節點開始構建節點然后再構建左子樹再構建右子樹，同樣左子樹的根節點繼續構建它的兩個子樹。
在這個過程中我們必須要有兩個信息：每次構建時根節點的值以及左右子樹在中序數組的范圍。
首先是根節點的值，這個我們可以通過后序數組來得到，右子樹的根節點下標我們只需要在當前的下標進行–就可以得到了，重點是左子樹的根節點的下標。

代碼

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:unordered_map<int,int> um;TreeNode* merge(int root,int left,int right,vector<int>& postorder){//結束的條件是左子樹的下標不小于右子樹if(left > right){return nullptr;}//構建節點TreeNode* node = new TreeNode(postorder[root]);//得到root位置在中序遍歷的下標int i = um[postorder[root]];//構建左子樹和右子樹//重點解釋一下左子樹的根節點怎么找//我們肯定也是在后序數組中找其次后序是左，右，根的順序//左子樹的根節點和當前樹的根節點只差了一個右子樹的長度//所以我們通過中序數組來找到右子樹的長度也就是right-i//因為right是有邊界，i是根節點在中序數組的下標所以right-i就是右子樹的長度//在減去右子樹的數量后我們還需要減1node->left = merge(root-(right-i)-1,left,i-1,postorder);node->right = merge(root-1,i+1,right,postorder);return node;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {//通過后序遍歷我們可以確定根節點的位置//通過中序遍歷我們可以得到該節點的左子樹和右子樹//所以我們可以使用分治的辦法將一棵樹從根節點開始向下構建for(int i = 0;i < inorder.size();i++){//記錄在中序遍歷中節點的值所對應的下標um[inorder[i]] = i;}return merge(postorder.size()-1,0,inorder.size()-1,postorder);}
};