相機的控制無非移動和旋轉，每種操作各3個軸6個方向，一共12種方式。在某些需要快速驗證的項目或Demo里常常需要絲滑的控制相機調試效果。相機控制雖然不是什么高深的技術，但是要寫的好用還是很磨人的。

鎖定Z軸的旋轉

一個自由的相機可以繞 X，Y，Z 軸旋轉，正常情況下用6個按鍵加上 transform.Rotate api 就可以搞定了。這里要注意的是要使用本地坐標系，transform.Rotate 默認就是本地坐標系。比如我們可以用上下左右方向鍵和鼠標左鍵來控制相機的旋轉。

void Update()
{if (Input.GetMouseButton(0)){var axis_x = Input.GetAxis("Mouse X") * 10;var axis_y = Input.GetAxis("Mouse Y") * 10;transform.localRotation *= Quaternion.Euler(-axis_y, axis_x, 0);}if (Input.GetKey(KeyCode.UpArrow)){transform.Rotate(Vector3.left, Time.deltaTime * 100);}else if (Input.GetKey(KeyCode.DownArrow)){transform.Rotate(Vector3.right, Time.deltaTime * 100);}if (Input.GetKey(KeyCode.LeftArrow)){transform.Rotate(Vector3.down, Time.deltaTime * 100);}else if (Input.GetKey(KeyCode.RightArrow)){transform.Rotate(Vector3.up, Time.deltaTime * 100);}
}

但是在某些情況下我希望實現一種類似第一人稱的視角，既相機可以左右看，上下看，但是不能歪頭，也就是要鎖定 Z 軸的旋轉。即便上面我們沒有 Z 方向的旋轉，但是實際上 X 軸和 Y 軸的旋轉也會引入 Z 軸的旋轉，讓人感覺相機極難控制，在不添加 Z 軸旋轉的情況下，相機很容易就歪了，還很難正回來。比如我們按上左下右的順序旋轉相機，當相機回到原點時，鏡頭已經歪到姥姥家了。

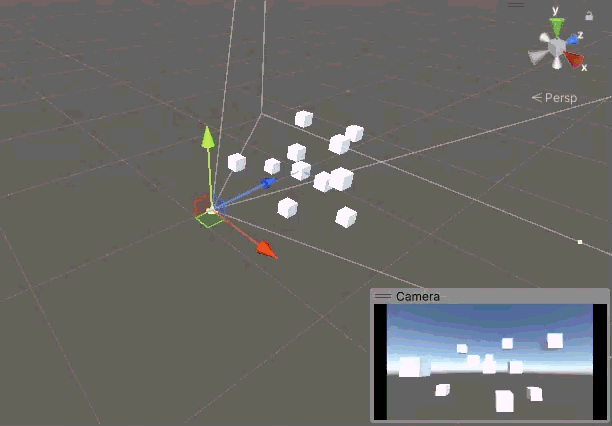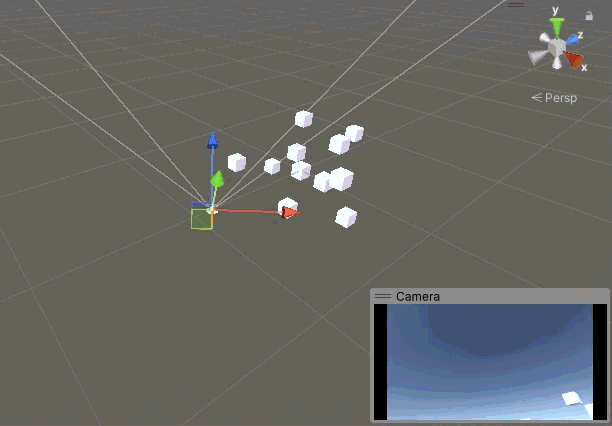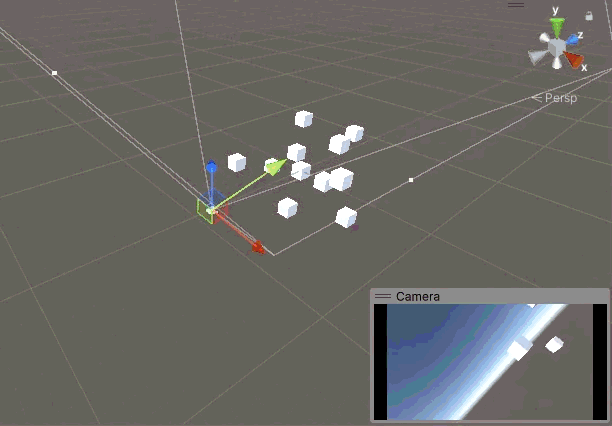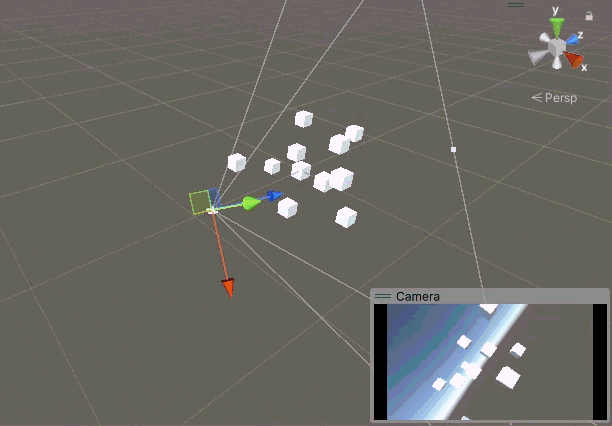
鎖定 Z 軸旋轉就是把 Z 向角度設置為0，我們添加一個鎖定 Z 軸的函數。

private void LockZRotate()
{var euler = transform.eulerAngles;euler.z = 0;transform.eulerAngles = euler;
}

然后在 Update 的最后調用 LockZRotate 即可。但是這樣也會有問題，繞 X 軸的旋轉在 ±90° 范圍內是正常的，一旦到達 90°，Z 軸向正上或正下，再繼續轉就轉不動了，視角會向電風扇一樣瘋轉旋轉。

雖然我們沒有旋轉 Z 軸，但是 Unity 會根據旋轉重新解算歐拉角，這種情況下繼續旋轉，經過 Unity 的解算，Z 軸上的角度就不是 0 了，但是我們又立刻將 Z 軸的角度置 0 了，導致 Unity 無法繼續旋轉，最終變成了直升機效果。

要邁過這道坎我們可以用世界坐標系去旋轉。也就是給 Rotate 函數加上 Space.World 參數，對于鼠標旋轉的情況，只需要將四元數的乘法順序調換一下就可以了。

void Update()
{if (Input.GetMouseButton(0)){var axis_x = Input.GetAxis("Mouse X") * 10;var axis_y = Input.GetAxis("Mouse Y") * 10;transform.rotation = Quaternion.Euler(-axis_y, axis_x, 0) * transform.rotation;}if (Input.GetKey(KeyCode.UpArrow)){transform.Rotate(Vector3.left, Time.deltaTime * 100, Space.World);}else if (Input.GetKey(KeyCode.DownArrow)){transform.Rotate(Vector3.right, Time.deltaTime * 100, Space.World);}if (Input.GetKey(KeyCode.LeftArrow)){transform.Rotate(Vector3.down, Time.deltaTime * 100, Space.World);}else if (Input.GetKey(KeyCode.RightArrow)){transform.Rotate(Vector3.up, Time.deltaTime * 100, Space.World);}LockZRotate();
}

Rotate 函數 Space.World 參數是指定旋轉軸的坐標空間的，Vector3.up + Space.World 相當于 transform.up + Space.Self 。

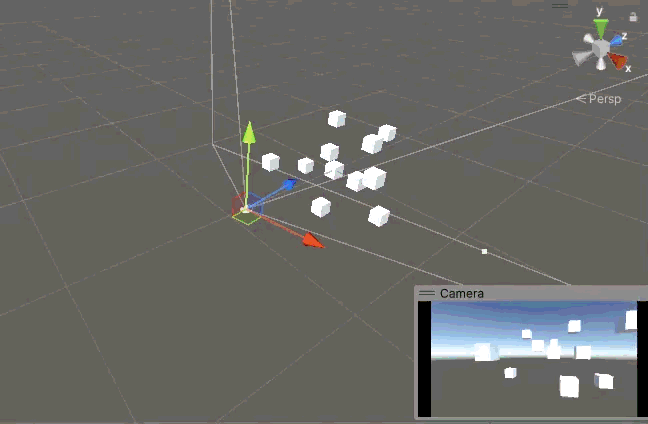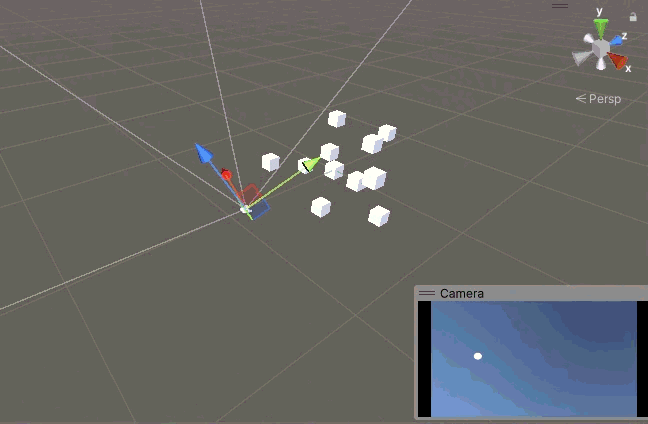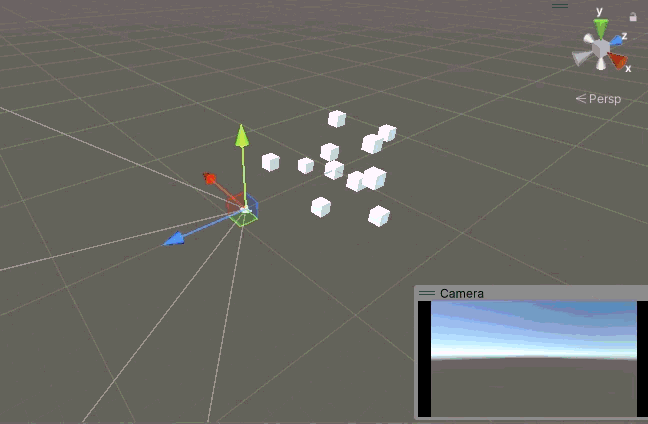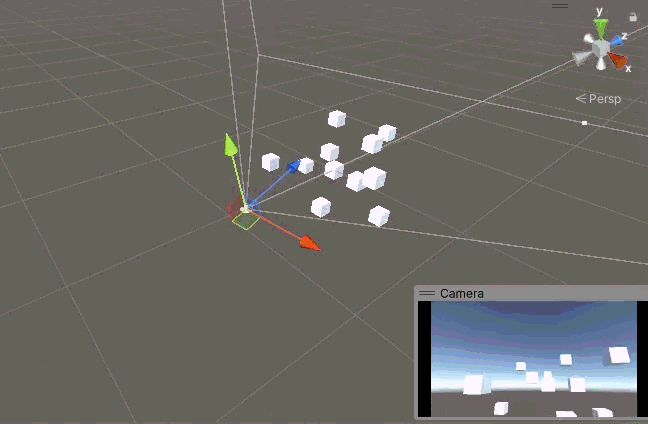
可以看到可以正常繞 X 軸旋轉超過 90°，而且相機始終是正的，天空始終在畫面上面。似乎是正常了，嚴格來說是當相機的 X 軸和世界的 X 軸重合的時候是正常的，也就是說其實還是不對。

當我們先繞 Y 軸旋轉 90° 后，此時相機的 Z 軸與世界的 X 軸重合，此時當我們再想繞 X 軸旋轉時，但實際上面的代碼變成了繞相機的 Z 軸旋轉，但是 Z 軸的旋轉被我們鎖定了，根本轉不動，于是相機 X 方向的旋轉就被鎖死在這里了。這只是最極端的情況，事實上當相機的 X 軸偏離世界的 X 軸時，X 方向的旋轉就都不正常了。

有一種辦法是把 X 軸的旋轉限制在 ±90° 范圍內，也就是不讓人“倒立”。可是妥協不是我想要的，我想要倒立，倒立過去之后還要保持鏡頭是正的。

回到最初按上左下右順序旋轉相機的例子，當我們在編輯模式下的 Inspector 面板中重復這個操作時，一切卻很正常，相機回到了原點，鏡頭也沒有歪。

唉？什么情況？

這并不是什么玄學，問題還是那個問題，Unity 會重新解算歐拉角。當我們在 Inspector 面板里面操作時，轉哪個軸就只轉那一個軸，不會重新解算，也不會動到其他軸，井水不犯河水。

這就意味這我們也可以模擬這個過程，手動記錄下相機的初始歐拉角，然后轉哪個軸就加減哪個角，最后將歐拉角賦值給相機就可以了。讓我們重新寫一個函數來專門負責旋轉。

public Vector3 euler;
private void RotateTransformAngle(float x = 0, float y = 0, float z = 0)
{euler.x = (euler.x + x) % 360;euler.y = (euler.y + y) % 360;euler.z = 0;transform.localEulerAngles = euler;
}

然后將旋轉也替換成這個函數，RotateTransformAngle 函數已經鎖定了 Z 軸，所以 LockZRotate 函數也不用再調用了。

void Update()
{if (Input.GetMouseButton(0)){var axis_x = Input.GetAxis("Mouse X") * 10;var axis_y = Input.GetAxis("Mouse Y") * 10;RotateTransformAngle(-axis_y, axis_x);}if (Input.GetKey(KeyCode.UpArrow)){RotateTransformAngle(x: -Time.deltaTime * 100);}else if (Input.GetKey(KeyCode.DownArrow)){RotateTransformAngle(x: Time.deltaTime * 100);}if (Input.GetKey(KeyCode.LeftArrow)){RotateTransformAngle(y: -Time.deltaTime * 100);}else if (Input.GetKey(KeyCode.RightArrow)){RotateTransformAngle(y: Time.deltaTime * 100);}//LockZRotate();
}

現在上左下右確實沒問題了，鏡頭不會再歪了，但是新的問題也出現了。當相機繞 X 軸旋轉 180° 時，我們真的“倒立”了，不能說沒有歪，簡直歪到極點了。

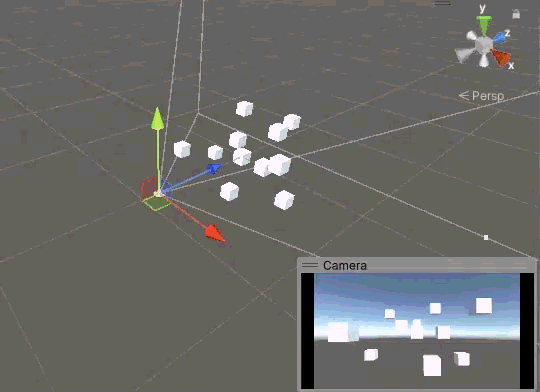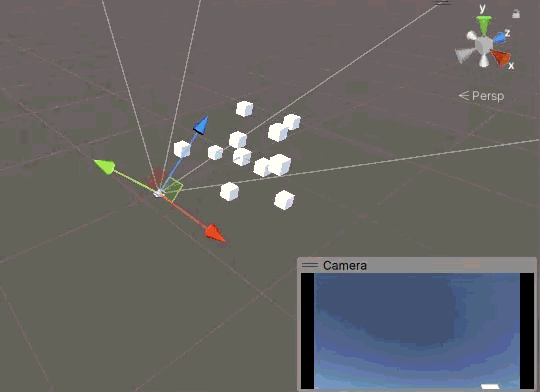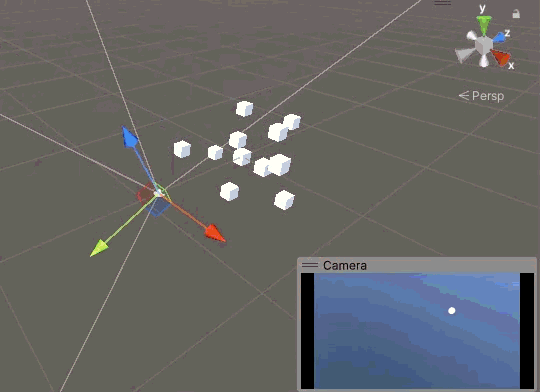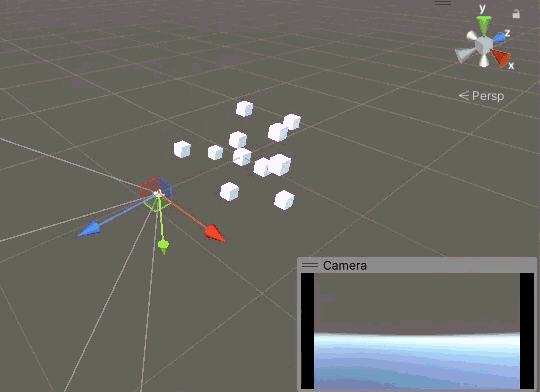
要讓相機鏡頭始終是正的，實際上等價于讓相機的 Y 軸始終朝上，可以把 Y 軸想象成人的頭，所謂的“正”，也就是人頭沖上。有什么東西是始終朝上的嗎？當然有，那就是世界的 Y 軸。我們可以加一個判斷，當相機的 Y 軸和世界的 Y 軸反向時，將相機的 Y 軸反轉，我們可以使用點乘來實現這個判斷。

private void RotateTransformAngle(float x = 0, float y = 0, float z = 0)
{euler.x = (euler.x + x) % 360;euler.y = (euler.y + y) % 360;euler.z = 0;transform.localEulerAngles = euler;if (Vector3.Dot(transform.up, Vector3.up) < 0){transform.rotation = Quaternion.LookRotation(transform.forward, -transform.up);}
}

嗯，現在我們會翻跟斗，但是不會倒立了。如果我們始終鎖定 Z 軸，到這里其實就可以結束了。但問題是并不是所有情況下我們都應該鎖定 Z 軸，萬一需要 Z 軸的旋轉呢？我們可以加一個開關來控制 Z 軸是否鎖定。

public bool lockz;
private void RotateTransformAngle(float x = 0, float y = 0, float z = 0)
{euler.x = (euler.x + x) % 360;euler.y = (euler.y + y) % 360;if (lockz){euler.z = 0;}else{euler.z = (euler.z + z) % 360;}transform.localEulerAngles = euler;if (lockz && (Vector3.Dot(transform.up, Vector3.up) < 0)){transform.rotation = Quaternion.LookRotation(transform.forward, -transform.up);}
}

然后我們還需要再添加兩個按鍵 Q 和 W 來旋轉 Z 軸，并在旋轉 Z 軸時，自動解鎖 Z 軸旋轉，順便加一個按鍵 z 來重新鎖定 Z 軸。

void Update() {...if (Input.GetKey(KeyCode.Q)){lockz = false;RotateTransformAngle(z: -Time.deltaTime * 100);}if (Input.GetKey(KeyCode.W)){lockz = false;RotateTransformAngle(z: Time.deltaTime * 100);}if (Input.GetKeyDown(KeyCode.Z)){lockz = true;}
}

這下總沒問題了，吧？當我們先繞 X 軸旋轉 180°，然后再轉動 Z 軸時，神奇的事情發生了，瞬間天地倒轉，又倒立了。

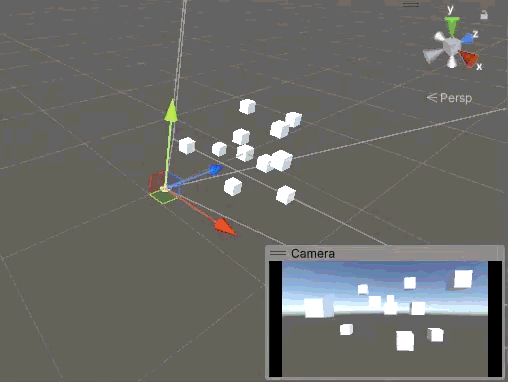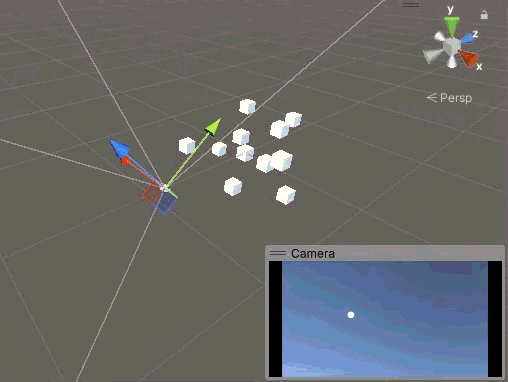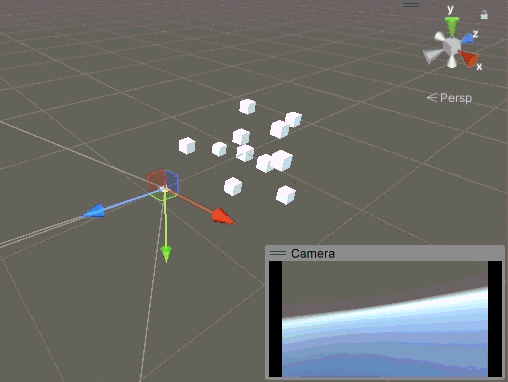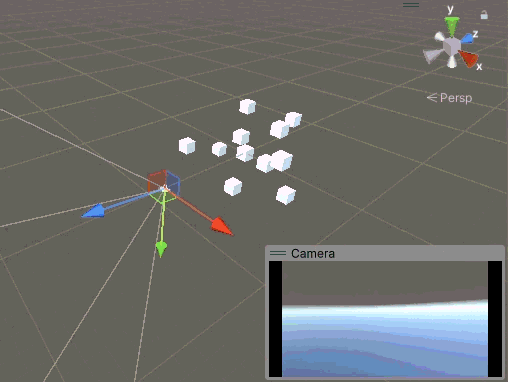
這個問題的原因很簡單，因為當我們繞 X 軸旋轉超過 90° 時，Y 軸發生了一次反轉，也就是相機繞 Z 軸旋轉了 180°，但是這個信息并未被記錄到我們手動管理的歐拉角中。此時當我們繞 Z 軸旋轉時，其實是基于未反轉的 Z 方向角度在修改，所以鏡頭會突然倒轉。

當鎖定 Z 軸時，Z 方向的歐拉角只有可能是 0° 或 180°，要解決這個問題，我們需要一個只有 0 和 1 兩種狀態的變量來記錄相機 Y 軸的翻轉狀態。1 bit 二進制數就剛好滿足我們的需求，只需要不斷的加一，它就會在 0 和 1 之間不斷翻轉。之所以要記錄下這個狀態，是因為當我們重新鎖定相機時，需要將 Z 向歐拉角恢復到解鎖前的狀態，而不是簡單的直接置 0。

public bool lockz;
public byte flipz;
private void RotateTransformAngle(float x = 0, float y = 0, float z = 0)
{euler.x = (euler.x + x) % 360;euler.y = (euler.y + y) % 360;euler.z = 0;if (lockz){euler.z = (flipz & 0x1) * 180;}else{euler.z = (euler.z + z) % 360;}transform.localEulerAngles = euler;if (lockz && (Vector3.Dot(transform.up, Vector3.up) < 0)){transform.rotation = Quaternion.LookRotation(transform.forward, -transform.up);euler.z = (flipz++ & 0x1) * 180;}
}

好了，這次是真的沒有問題了。

移動速度加成

相機移動相比于旋轉要簡單的多，直接使用 transform.Translate 函數就可以了，而且每個方向都可以自由移動。

與旋轉不同的是移動的范圍要更廣闊，對于旋轉，每個軸的旋轉角度只會在 0 ~ 360° 之間，但是移動的范圍幾乎是無限的。這就帶來了一個問題，當我們想移動很遠的距離時，要“走”很久才能到。

簡單，走快點就好了。但是也不能一開始就走很快，因為我們并不能確定當用戶按下移動鍵時，是想去很遠的地方，還是只想湊近一點。因此啟動速度不能太快，否則我們很難準確控制相機到達想去的地方。

解決這個問題我們可以記錄下用戶按下移動鍵的時長，然后根據按鍵按下的時間計算一個移動速度加成。剛開始時沒有任何加成，如果用戶一直按著鍵盤不撒手，那就逐漸給一個更大加成，讓相機移動的越來越快。最后當加成到達一個上限時，保持住不在變大。

你可能已經想到了，這不就是一個分段函數嗎？的確，我們需要的確實是一個分段函數。
$$y=?\begin{array}{ll}1& x<a\\ x& a<x<b\\ 10& x>b\end{array}$$

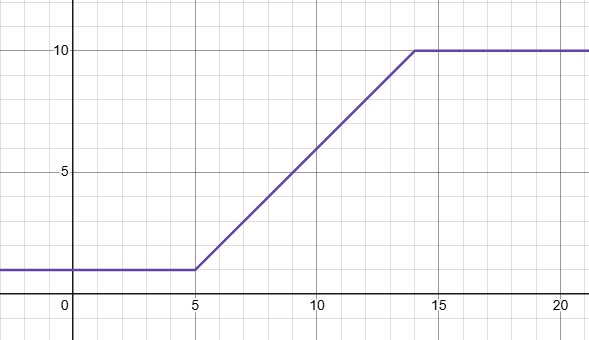
但是分段函數是不平滑的，而且我們還想讓變化有一些非線性。有這么一個函數，在 $x=0$ 附近函數值為 $1$，隨著 $x$ 的增大，函數值逐漸增大，最后在 $+\infty$ 處趨于 $1$。
$$y=e^{?\frac{1}{x^2}}$$

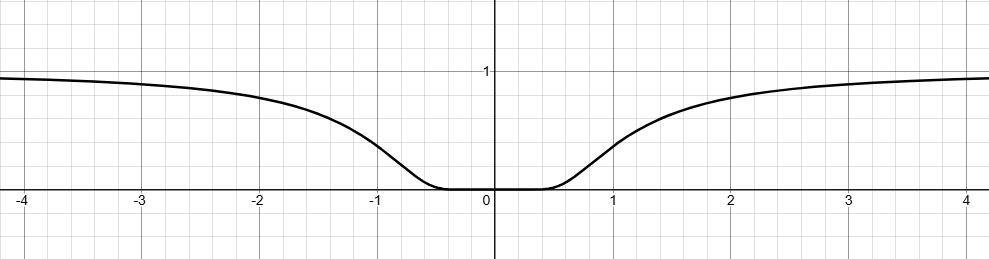
因為函數值在 $[0,1]$ 范圍內，因此我們很容易把他縮放到 $[1,M]$ 范圍內。同時我們還可以加一些參數來調整函數的增長速度和底部寬度。
$$y=1+(M?1)e^{?\frac{t}{x^r}}$$
除了鍵盤操作，用鼠標滾輪來前后移動相機也是實用的操作，此時我們在算加成時，不是用滾動時間，而是用滾輪連續同方向滾動的距離。

goto與環繞

除了移動與旋轉，我們還可以實現一些快捷操作，比如用鼠標點擊一個點，讓相機看向并移動到這個點“前面”，或者移動相機變成環繞這個點移動。這些功能的實現并不難，使用 LookAt 和 RotateAround 就能實現了。需要注意的是要讓相機平滑的看向并移動到目標點，需要進行插值，否則鏡頭會生硬的跳過去。

最終我們會實現下面的功能：

鼠標	按鍵	功能
左鍵		上下左右旋轉相機
	↑ ↓ ← →	上下左右旋轉相機
滾輪	X Y Z	繞指定軸旋轉相機
左鍵	A D L-Shift Space	相機上下左右環繞點擊的點
	W S A D L-Shift Space	相機前后左右上下移動
滾輪		相機前后移動
中鍵		相機上下左右移動
右鍵		相機Goto點擊的點
	Z	鎖定 Z 軸旋轉

源碼

源碼以 .unitypackage 的形式放到了CSDN，可以直接導入使用。

https://download.csdn.net/download/puss0/91565511