目錄

搜索二維矩陣Ⅱ

題目描述

題解

解法一：暴力搜索

C++ 代碼實現

復雜度分析

解法二：二分查找

C++ 代碼實現

復雜度分析

解法三：Z字形查找

算法核心思想

算法步驟詳解

C++ 代碼實現

復雜度分析

---

搜索二維矩陣Ⅱ

題目描述

編寫一個高效的算法來搜索 m x n 矩陣 matrix 中的一個目標值 target 。該矩陣具有以下特性：

每行的元素從左到右升序排列。 每列的元素從上到下升序排列。

示例 1：

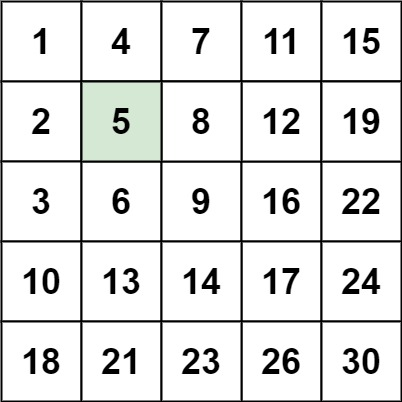
輸入：matrix = [ [1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30] ], target = 5
輸出：true

示例 2：

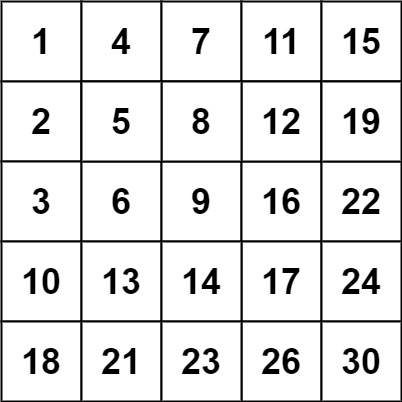
輸入：matrix = [ [1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30] ], target = 20 輸出：false

提示：
每行的所有元素從左到右升序排列
每列的所有元素從上到下升序排列

題解

解法一：暴力搜索

暴力搜索的思路是遍歷矩陣的所有元素，并判斷當前元素是否等于目標值。時間復雜度為 O(mn)。

C++ 代碼實現

class Solution:{
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {int m = matrix.size();int n = matrix[0].size();for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (matrix[i][j] == target) {return true;}}}return false;
}
};

復雜度分析

• 時間復雜度：O(mn)，遍歷矩陣的所有元素。
• 空間復雜度：O(1)，不使用額外空間。

解法二：二分查找

由于矩陣 matrix 中每一行的元素都是升序排列的，因此我們可以對每一行都使用一次二分查找，判斷 target 是否在該行中，從而判斷 target 是否出現。

C++ 代碼實現

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {for (const auto& row : matrix) {if(binary_search(row.begin(), row.end(), target)) {return true;  }}return false;}};

復雜度分析

• 時間復雜度：O(mlogn)，對每一行使用一次二分查找，時間復雜度為 O(logn)。
• 空間復雜度：O(1)，不使用額外空間。

解法三：Z字形查找

算法核心思想

Z字形查找是一種線性時間復雜度的搜索算法，專門用于搜索行列都有序的二維矩陣。
它的核心思想是： 從矩陣的右上角開始搜索 利用矩陣的有序性質，每次可以排除一整行或一整列 搜索路徑形成"Z"字形，因此得名

算法步驟詳解

步驟 1: 初始化位置
從右上角 (0, n-1) 開始，這個位置有特殊性質：
向左移動：值變小
向下移動：值變大
步驟 2: 比較與移動
if (matrix[x][y]?== target) → 找到目標，返回 true
if (matrix[x][y]?> target) → 當前值太大，向左移動 (y--)
if (matrix[x][y]?< target) → 當前值太小，向下移動 (x++)
步驟 3: 邊界檢查
如果超出邊界 (x >= m || y < 0)，說明目標不存在

C++ 代碼實現

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m = matrix.size(), n = matrix[0].size();int x = 0, y = n - 1; // 從右上角開始while (x < m && y >= 0) {if (matrix[x][y] == target) {return true; // 找到目標}if (matrix[x][y] > target) {--y; // 當前值太大，向左移動} else {++x; // 當前值太小，向下移動}}return false; // 超出邊界，未找到}
};

復雜度分析

• 時間復雜度：O(m+n)。在搜索的過程中，如果我們沒有找到 target，那么我們要么將 y 減少 1，要么將 x 增加 1。由于 (x,y) 的初始值分別為 (0,n?1)，因此 y 最多能被減少 n 次，x 最多能被增加 m 次，總搜索次數為 m+n。在這之后，x 和 y 就會超出矩陣的邊界。

• 空間復雜度：O(1)，不使用額外空間。