深度學習 – 梯度計算及上下文控制

---

一，自動微分

自動微分模塊torch.autograd負責自動計算張量操作的梯度，具有自動求導功能。自動微分模塊是構成神經網絡訓練的必要模塊，可以實現網絡權重參數的更新，使得反向傳播算法的實現變得簡單而高效。

1.1 基礎概念

1. 張量

   Torch中一切皆為張量，屬性requires_grad決定是否對其進行梯度計算。默認是 False，如需計算梯度則設置為True。

2. 計算圖：

   torch.autograd通過創建一個動態計算圖來跟蹤張量的操作，每個張量是計算圖中的一個節點，節點之間的操作構成圖的邊。

   在 PyTorch 中，當張量的 requires_grad=True 時，PyTorch 會自動跟蹤與該張量相關的所有操作，并構建計算圖。每個操作都會生成一個新的張量，并記錄其依賴關系。當設置為 True 時，表示該張量在計算圖中需要參與梯度計算，即在反向傳播（Backpropagation）過程中會自動計算其梯度；當設置為 False 時，不會計算梯度。

• 計算依賴圖
  
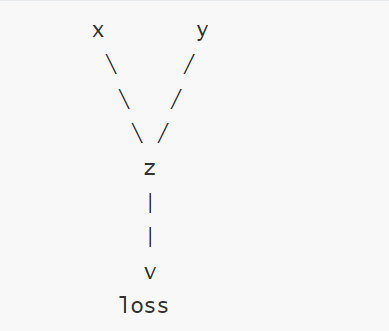
  葉子結點判斷方式

x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)  # 葉子節點
y = x ** 2  # 非葉子節點（通過計算生成）
z = y.sum()print(x.is_leaf)  # True
print(y.is_leaf)  # False
print(z.is_leaf)  # False

1.2 計算梯度

使用tensor.backward()方法執行反向傳播，從而計算張量的梯度

1.2.1 計算標量梯度

import torchdef test01():x= torch.tensor(1.0,requires_grad=True)# requires_grad=True表示需要求導y=x**2# 操作張量y.backward() #計算梯度，也就是反向傳播print(x.grad) # 打印梯度if __name__ == '__main__':test01()

1.2.2 計算向量梯度

def test002():# 1. 創建張量：必須為浮點類型x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)y = x ** 2loss = y.mean()loss.backward()print(x.grad)if __name__ == "__main__":test002()

調用 loss.backward() 從輸出節點 loss 開始，沿著計算圖反向傳播，計算每個節點的梯度。

損失函數$$loss=mean(y)=\frac{1}{n}\sum _{i=1}^n{y}_i$$，其中 n=3。

對于每個 $y_i$，其梯度為 $\frac{?loss}{?y_i}=\frac{1}{n}=\frac{1}{3}$。

對于每個 $x_i$，其梯度為：
$$\frac{?loss}{?x_i}=\frac{?loss}{?y_i}\times \frac{?y_i}{?x_i}=\frac{1}{3}\times 2x_i=\frac{2x_i}{3}$$
所以，x.grad 的值為：$[\frac{2\times 1.0}{3},\frac{2\times 2.0}{3},\frac{2\times 3.0}{3}]=[\frac{2}{3},\frac{4}{3},2]\approx [0.6667,1.3333,2.0000]$

1.2.3 多標量梯度計算

#多標量梯度計算
def test03():x1= torch.tensor(1.0,requires_grad=True)x2=torch.tensor(3.0,requires_grad=True)y=x1**2+x2*7z=y.sum()z.backward()print(x1.grad,x2.grad)if __name__ == '__main__':test03()

1.2.4 多向量梯度計算

# 多向量梯度計算
def test04():x1 = torch.tensor([1.0, 2.0], requires_grad=True)x2 = torch.tensor([3.0, 4.0], requires_grad=True)y = x1 ** 2 + x2 * 7z = y.sum()z.backward()print(x1.grad, x2.grad)if __name__ == '__main__':test04()

二，梯度上下文控制

梯度計算的上下文控制和設置對于管理計算圖、內存消耗、以及計算效率至關重要。下面我們學習下Torch中與梯度計算相關的一些主要設置方式。

2.1 控制梯度計算

簡單的運算不需要梯度

import torchdef test01():x=torch.tensor(11.5,requires_grad=True)print(x.requires_grad)# Truey=x**2print(y.requires_grad)# Truewith torch.no_grad():z=x**2print(z.requires_grad)#使用裝飾器@torch.no_grad()def test():return x**2y=test()print(y.requires_grad)if __name__ == '__main__':test01()

2.2 累計梯度

默認情況下，當我們重復對一個自變量進行梯度計算時，梯度是累加的

import torchdef test002():x = torch.tensor([1.0, 2.0, 5.3], requires_grad=True)# 2. 累計梯度：每次計算都會累計梯度for i in range(3):y = x**2 + 2 * x + 7z = y.mean()z.backward()print(x.grad)if __name__ == "__main__":test002()

2.3 梯度清零

大多數情況下是不需要梯度累加的

#梯度清零
def test002():x = torch.tensor([1.0, 2.0, 5.3], requires_grad=True)# 2. 累計梯度：每次計算都會累計梯度for i in range(3):y = x**2 + 2 * x + 7z = y.mean()# 2.1 反向傳播之前先對梯度進行清零if x.grad is not None:x.grad.zero_()z.backward()print(x.grad)if __name__ == "__main__":test002()

三，案例一----求函數最小值

import torch
from matplotlib import pyplot as plt
import numpy as npdef test01():x = np.linspace(-10, 10, 100)y = x ** 2plt.plot(x, y)plt.show()def test02():# 初始化自變量Xx = torch.tensor([3.0], requires_grad=True, dtype=torch.float)# 迭代輪次epochs = 50# 學習率lr = 0.1list = []for i in range(epochs):# 計算函數表達式y = x ** 2# 梯度清零if x.grad is not None:x.grad.zero_()# 反向傳播y.backward()with torch.no_grad():x -= lr * x.gradprint('epoch:', i, 'x:', x.item(), 'y:', y.item())list.append((x.item(), y.item()))# 散點圖，觀察收斂效果x_list = [l[0] for l in list]y_list = [l[1] for l in list]plt.scatter(x=x_list, y=y_list)plt.show()if __name__ == "__main__":test01()test02()

四，案例二----函數參數求解

import torchdef test02():x = torch.tensor([1, 2, 3, 4, 5], dtype=torch.float)y = torch.tensor([3, 5, 7, 9, 11], dtype=torch.float)a = torch.tensor([1.0], dtype=torch.float, requires_grad=True)b = torch.tensor([1.0], dtype=torch.float, requires_grad=True)lr = 0.05epochs = 1000for epoch in range(epochs):y_pred = a * x + bloss = ((y_pred - y) ** 2).mean()if a.grad is not None:a.grad.zero_()if b.grad is not None:b.grad.zero_()loss.backward()with torch.no_grad():a -= lr * a.gradb -= lr * b.gradif (epoch + 1) % 100 == 0:print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')print(f'a: {a.item():.4f}, b: {b.item():.4f}')if __name__ == '__main__':test02()