IP復原(難)
力扣鏈接:IP復原
題目:有效 IP 地址 正好由四個整數(每個整數位于 0 到 255 之間組成,且不能含有前導 0),整數之間用 '.' 分隔。
- 例如:
"0.1.2.201"和"192.168.1.1"是 有效 IP 地址,但是"0.011.255.245"、"192.168.1.312"和"192.168@1.1"是 無效 IP 地址。
給定一個只包含數字的字符串 s ,用以表示一個 IP 地址,返回所有可能的有效 IP 地址,這些地址可以通過在 s 中插入 '.' 來形成。你 不能 重新排序或刪除 s 中的任何數字。你可以按 任何 順序返回答案。
思路:
回溯三問{當前操作?枚舉分隔符‘.’的位置(有三種情況,長度1,2,3)子問題?從下標≥j的后綴中繼續修復IP下一個子問題?從下標≥j+1的后綴中繼續修復IP回溯三問\left\{\begin{array}{l}\text {當前操作?枚舉分隔符‘.’的位置(有三種情況,長度1,2,3)} \\ \text {子問題?從下標} \geq j \text {的后綴中繼續修復IP} \\ \text {下一個子問題?從下標} \geq j+1\text {的后綴中繼續修復IP}\end{array}\right. 回溯三問????當前操作?枚舉分隔符‘.’的位置(有三種情況,長度1,2,3)子問題?從下標≥j的后綴中繼續修復IP下一個子問題?從下標≥j+1的后綴中繼續修復IP?
判斷IP合法,即所枚舉分割的字符串(從i開始,長度枚舉)
- 開頭不為0(注意,這里是當長度大于1才有的約束,單單一個0完全可以,01就不行)
- 轉換成的數字小于等于255
邊界情況
最后可能剩余長度不到3了
比如長度為4 ,i為3,j只能為1,即i+j>n會越界
注意這里:substr(i,j),這里從下標為i的開始,長度為j,i為3說明前面有三個元素,所以i+j>n時才越界,而不是i+j≥n就越界
這里使用了vector<string>來定義路徑,而不是string,優點有兩個
- 可以在最后統一處理“.”,而不是每次加入path時就+”.“,不需要在最后一步額外再處理”.“
- 回溯方便,pop()即可,不需要使用earse函數
stoi(),C++內置字符串轉整型
class Solution {
public:vector<string> restoreIpAddresses(string s) {int n = s.size();vector<string> result;vector<string> path;if (n < 4 || n > 12)return {};auto dfs = [&](this auto&& dfs, int i) {if (i == n && path.size() == 4) {result.emplace_back(path[0] + '.' + path[1] + '.' + path[2] +'.' + path[3]);return;}// 剪枝函數,如果剩余字符數小于剩余段數,或者剩余字符數大于剩余段數乘以3,則不可能構成有效的IP地址if (n - i < 4 - path.size() || n - i > 3 * (4 - path.size()))return;for (int j = 1; j <= 3; j++) {if (i + j >n)break;string sub = s.substr(i, j);if (sub[0] == '0' && j > 1) //continue;if (std::stoi(sub) > 255)continue;path.emplace_back(sub);dfs(i + j);path.pop_back();}};dfs(0);return result;}
};
全排列
力扣鏈接:全排列
題目:給定一個不含重復數字的數組 nums ,返回其 所有可能的全排列 。你可以 按任意順序 返回答案。
思路:
回溯三問{當前操作?枚舉nums中未使用過的元素子問題?構造path的≥i+1的部分,剩余元素為{nums}-{x1}下一個子問題?繼續構造path的≥i+1的部分,剩余元素為{nums}-{x2}回溯三問\left\{\begin{array}{l}\text {當前操作?枚舉nums中未使用過的元素} \\ \text {子問題?構造path的≥i+1的部分,剩余元素為\{nums\}-\{x1\}} \\ \text {下一個子問題?繼續構造path的≥i+1的部分,剩余元素為\{nums\}-\{x2\}}\end{array}\right. 回溯三問????當前操作?枚舉nums中未使用過的元素子問題?構造path的≥i+1的部分,剩余元素為{nums}-{x1}下一個子問題?繼續構造path的≥i+1的部分,剩余元素為{nums}-{x2}?
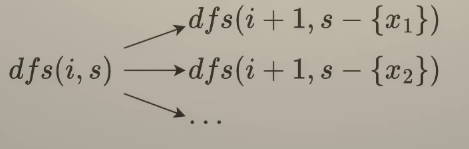
與之前的組合不同,這道題可以往回遍歷,比如【1,2,3】,當遍歷到元素2時,只要元素1未使用就可以接著添加到中,【1,2】,【2,1】是不同的答案,因此整體的不同之處(從答案的角度看)
-
每次選擇路徑元素都要將
nums整體從頭遍歷一遍 -
需要一個used保存已經使用過的元素,保證從頭遍歷時不會出現重復
如何選擇去重集合used,直接使用used結合去重?自定義標記使用元素
錯誤寫法,使用增強for循環時只能遍歷,不能修改集合,迭代器指針指向會出現問題
for (int i:unused) { //for增強循環path.push_back(i);unused.erase(i);//修改集合dfs();unused.insert(i);//修改集合
}
現在就存在了問題,要遍歷就不能實現回溯,不能同時實現
所以:只能使用自定義標記 bool數組false或true區別
class Solution {
public:vector<vector<int>> permute(vector<int>& nums) {vector<int> path;vector<vector<int>> result;bool used[6] = {false};int n = nums.size();auto dfs = [&](this auto&& dfs, int i) {if (i == n) {result.push_back(path);return;}for (int j = 0; j < n; j++) {if (used[j]) //使用過的元素不在使用continue;path.push_back(nums[j]);used[j] = true;dfs(i + 1);//回溯時記得連同使用過的元素一起回溯path.pop_back();used[j] = false;}};dfs(0);return result;}
};
全排列II
力扣鏈接:全排列II
題目:給定一個可包含重復數字的序列 nums ,按任意順序 返回所有不重復的全排列。
相較于全排列nums中有重復元素了
回溯三問{當前操作?枚舉nums中未使用過,且本層未使用過的元素子問題?構造path的≥i+1的部分,剩余元素為{nums}-{x1}下一個子問題?繼續構造path的≥i+1的部分,剩余元素為{nums}-{x2}回溯三問\left\{\begin{array}{l}\text {當前操作?枚舉nums中未使用過,\textcolor{red}{且本層未使用過的元素}} \\ \text {子問題?構造path的≥i+1的部分,剩余元素為\{nums\}-\{x1\}} \\ \text {下一個子問題?繼續構造path的≥i+1的部分,剩余元素為\{nums\}-\{x2\}}\end{array}\right. 回溯三問????當前操作?枚舉nums中未使用過,且本層未使用過的元素子問題?構造path的≥i+1的部分,剩余元素為{nums}-{x1}下一個子問題?繼續構造path的≥i+1的部分,剩余元素為{nums}-{x2}?
思路:
思考:上一道題與非遞減子序列的結合
只需要在上一道題的基礎上加個本層去重即可,
應該?排序?+?相同?元素?跳過?或者?每?層?s?et?集合去重均可🤔
這里使用set集合去重
即bool數組用于避免同一個元素使用兩次,set集合用于避免出現同一種排列(本層同一種(不是同一個元素選兩次)
class Solution {
public:vector<vector<int>> permuteUnique(vector<int>& nums) {vector<vector<int>> result;vector<int> path;bool used[8] = {false}; // 此元素使用過int n = nums.size();auto dfs = [&](this auto&& dfs, int i) {if (i == n) {result.push_back(path);return;}unordered_set<int> curUsed; // 相等元素本層使用過for (int j = 0; j < n; j++) {if (used[j] || curUsed.find(nums[j]) != curUsed.end())continue;path.push_back(nums[j]);used[j] = true;curUsed.insert(nums[j]);dfs(i + 1);//回溯,因為set記錄的是本層的重復元素,所以不需要回溯path.pop_back();used[j] = false;}};dfs(0);return result;}
};
N皇后
力扣鏈接:N皇后
題目:按照國際象棋的規則,皇后可以攻擊與之處在同一行或同一列或同一斜線上的棋子。
n 皇后問題 研究的是如何將 n 個皇后放置在 n×n 的棋盤上,并且使皇后彼此之間不能相互攻擊。
給你一個整數 n ,返回所有不同的 n 皇后問題 的解決方案。
每一種解法包含一個不同的 n 皇后問題 的棋子放置方案,該方案中 'Q' 和 '.' 分別代表了皇后和空位。
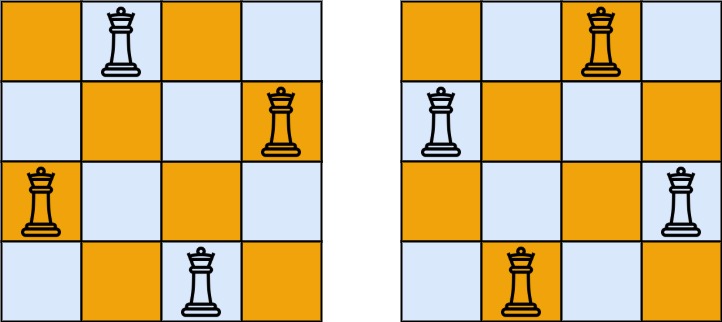
思路:
與全排列類似,是枚舉列號的全排列,舉例,即[1,2,3,4]的全排列,數組的下標代表行號,內容代表列號,
在此基礎上加了兩個難點
- 最終結果的輸出[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
- 遍歷保存了每一行queen位置的queens數組,queen在第幾列,就構造一個n個"."的字符串,同時構造一個n-1-queen(加起來一共是n個字符)位置個“.”字符串,兩者通過一個Q進行拼接,即為答案
- 每一組全排列要額外滿足不在對角線上
- 很巧妙很巧妙,復制的靈神的
- 首先對角線分為兩類,主對角線和副對角線,需要構造兩個數組分別存儲
- 其次,對于同一條對角線,
- 副對角線(左下到右上):行數 +列數(r+c)相等,想象一下,r每-1,c就+1。
范圍【0,n*2-2】,因為r【0,n-1】,c【0,n-1】,兩者相加的范圍就是【0,2*n-2】 - 主對角線(左上到右下):行數 - 列數(r-c)相等,因為,同一條對角線上 r每+1,c就+1。
范圍【-(n-1),n-1】,因為r【0,n-1】,-c【-(n-1),0】,兩者相加的范圍就是【-(n-1),n-1】
- 副對角線(左下到右上):行數 +列數(r+c)相等,想象一下,r每-1,c就+1。
- 基于以上思考,可以兩者均定義為n*2-1的數組,副對角線計算時直接r+c即可,主對角線計算時為避免負索引,需要r-c+n-1
處理完這兩個難點,這道題就和全排列的解決步驟相同了
class Solution {
public:vector<vector<string>> solveNQueens(int n) {vector<vector<string>> ans;vector<int> queens(n); // queens 數組用于存儲皇后的位置,queens[r] 表示第 r 行的皇后放在了第 queens[r] 列//這里標記位置的col,diag本來bool類型即可,但是靈神說int效率更高vector<int> col(n);// col 數組用于標記每一列是否已經被占用vector<int> diag1(n * 2 - 1); // diag1 數組用于標記副對角線(左下到右上)是否已經被占用// r + c 的值在同一條副對角線上是相同的vector<int> diag2(n * 2 - 1); // diag2 數組用于標記主對角線(左上到右下)是否已經被占用// r - c + n - 1 的值在同一條主對角線上是相同的auto dfs = [&](this auto&& dfs, int r) {//結束if (r == n) {//將queens數組生成字符串,并整合為答案vector<string> board(n);for (int i = 0; i < n; i++) {// 使用字符串構造函數生成一行,先生成 queens[i] 個 '.',然后是 'Q',最后是 n - 1 - queens[i] 個 '.board[i] = string(queens[i], '.') + 'Q' + string(n - 1 - queens[i], '.');}ans.push_back(board);return;}// 在第 r 行的每一列嘗試放置皇后for (int c = 0; c < n; c++) {// 計算當前位置所在的副對角線的索引int rc = r - c + n - 1;// 如果當前列和兩條對角線都沒有被占用,說明可以在當前位置放置皇后if (!col[c] && !diag1[r + c] && !diag2[rc]) { //!col[c]即為與全排列的元素不能重復的邏輯實現queens[r] = c;// 標記當前列和兩條對角線已經被占用col[c] = diag1[r + c] = diag2[rc] = true;// 遞歸調用 dfs,嘗試在下一行放置皇后dfs(r + 1);// 恢復現場,回溯到上一步,嘗試在其他位置放置皇后col[c] = diag1[r + c] = diag2[rc] = false;}}};dfs(0);return ans;}
};
解數獨
力扣鏈接:解數獨
題目:編寫一個程序,通過填充空格來解決數獨問題。
數獨的解法需 遵循如下規則:
- 數字
1-9在每一行只能出現一次。 - 數字
1-9在每一列只能出現一次。 - 數字
1-9在每一個以粗實線分隔的3x3宮內只能出現一次。(請參考示例圖)
數獨部分空格內已填入了數字,空白格用 '.' 表示。
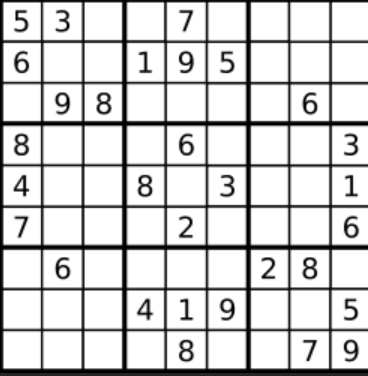
思路:
難點:
- 當前位置枚舉數字的合法性檢測
- 二維遞歸
合法性檢測:3X3范圍內只出現一次?
可以先將范圍定位到就九個中棋盤,即row/3定位到縱向三個位置中的一個,同理col也是,0,即代表前面有0個粗化的行(即3個細行),其他同理
定位到中位置后,再進一步將大體位置細化到具體的起始行和列,將原來的大體位置*3即可,因為一個行號或者列號對應三個細化的行和列,
以行為例,【0,1,2】分別即對應【0,3,6】
然后知道起始行也知道長度,遍歷九宮格即可
for (int i = startRow; i < startRow + 3; i++) { // 判斷9方格里是否重復for (int j = startCol; j < startCol + 3; j++) {if (board[i][j] == val) {return false;}}}
二維遞歸
要始終明白,下一個子問題是從填充后面所有位置,而不是填充從下一行開始到結束的所有位置
名稱一樣二維遞歸
auto dfs = [&](this auto&& dfs, int row) -> bool {for(int i = row; i < 9; i++) //(上一層填充了一個位置)從當前行開始重新遍歷,更好的做法是直接定位到某行某列,//但是不易于實現和理解for (int j = 0; j < 9; j++) {if (board[i][j] == '.') {for (char num = '1'; num <= '9'; num++) {if (isValid(i, j, num, board)) {board[i][j] = num;if (dfs(i)) //深入判斷,只有此處一直為真才會返回真,//當路徑偏差時(即上一層為真,但是導致下一層所有數字都不可填入時),會返回假return true;board[i][j] = '.';}}//無論前面是否填充,進行到這一步就返回false,//當前面九個數字都不滿足時返回 false//一旦有數字滿足就會深入分支,進行進一步深入判斷,return false;}}//遍歷結束,直接返回真即可,只要遍歷到最后,說明前面都符合,//中途一個位置出現了所有數字都不能填充當前位置時(即填充行為無法進行時),就會return falsereturn true;};
——變分自編碼器詳解與實現)



![[AI-video] 數據模型與架構 | LLM集成](http://pic.xiahunao.cn/[AI-video] 數據模型與架構 | LLM集成)














)