前言
我在之前的文章中提到過多次,長沙具身團隊是我司建設的第二支具身團隊,通過5月份的全力招聘,為了沖刺6月底和7月初來長沙辦公室考察的第一批客戶,過去一個多月來,長沙分部(一開始就5人,另外5人 + 實習生后面才逐個逐個進來的) 高速發展
| 機械臂(6月份側重的機械臂) | 人形(7月份則將側重人形) | |
| 陸續到位一系列設備 | 25年6.4日,正值我司注冊十周年,在沒動南京那邊機器的情況下,到位了piper機械臂和宇樹G1 edu 之后的6.6日,再到齊VR和吊架 | |
| 先后完成各種方式遙操機械臂 | 6.8日,在新同事們分的其中一個兩人小組上,VR已可遙操piper 6.9-6.13,長沙具身團隊先后完成通過鍵盤、手柄、VR、主從臂遙操piper機械臂的工作 | |
| 機械臂之外,開干人形 | 6.16,人形的所有配套硬件 基本全部補齊,比如vr外的:雙目及深度相機 + 3d打印件,開始正式開發g1 edu 6.18 我司「七月在線」長沙分部那邊,以同事朝陽為主力,我打雜,折騰了整整一天,終于可以通過VR搖操宇樹G1了——當然,搖操是為了做訓練數據的采集,從而方便 下一步的模型(策略)訓練,最終實現機器人自主做各種任務 | |
| 機械臂上 開始陸續一系列科研復現成功 | 6.23,長沙分部新同事們完成其中一個練手項目,lerobot ACT自主抓個杯子 6.24,長沙分部幾個新同事的完成又一個練手項目:抓零食 6.25,開始挑戰一個難點的任務,先采數據 訓練模型 最后:自主抓耳機線 插主機的耳機孔 | |
| 人形上 也開始出成果了 | 6.26日晚上,我們搞定了讓機器人跳舞,且在我司長沙辦公室現場讓宇樹G1跳查爾斯頓舞 且第二天,25年6.27上午,我們再次在長沙辦公室給某車企客戶演示了這個查爾斯頓舞 | |
| 機械臂上挑戰難度更大、精度更高的任務 | 6.29,歷時一周多,我們(同事文弱為主)通過基于uc伯克利的RL項目hil-serl,成功實現在仿真中抓方塊(成功率基本100%),respect kewang 6.30,我司長沙分部挑戰并完成了難度更高的任務——耳機線插耳機孔(這個任務是我們自己想出來的),成了,自主模式下,無任何搖操 7.4,通過單純模仿學習且不加觸覺情況下,使得耳機插孔的成功率達到了80% 7.11,上個月機械臂上的任務,都是用的lerobot那套框架(包含ACT和pi0),本周(7.7-7.11)完成了官方openpi在臂上的部署(訓練+推理),練手一個簡單任務:抓零食 相當于因為團隊以前經驗的積累,加上有朋友的幫助 3天完成openpi在國產臂上的部署 + 數采,2天完成訓練、推理 7.12,昨天通過openpi抓零食,今天又訓了一個任務,openpi自主做智能分揀 即便被分揀物體被交換了位置,也能成功分揀,畢竟vla還是比單純il更智能些 | 人形上 7.12,除了機械臂上的各種操作外,人形也一直在做各種二次開發,比如這兩天在宇樹sdk基礎上,做了下大模型對話功能 |
本文解讀UC伯克利最近新提出來的一個工作

- 其對應的項目地址為:colinqiyangli.github.io/qc
其GitHub地址為:github.com/colinqiyangli/qc - 其paper地址為:https://arxiv.org/abs/2507.07969
一作是UC伯克利的博士生,二作也是UC伯克利的博士生且同時是PI的實習生,三作則是UC伯克利的副教授,且同時是PI的聯創
PS,白天,我粗略統計了一下
- 過去一年(24年7月-25年7月),看的具身相關的論文大概是186篇,當然,不是每一篇都做了精讀,值得精讀的,大部分也在博客中解讀了
- 當一個方向讀了兩三百篇論文之后,這個方向而言,便沒有大的秘密了,但 還有很多小秘密
??所以還得不斷的讀,且和團隊不斷的落地實踐,也期待與更多具身同仁、同行多多合作
第一部分
1.1 引言、相關工作、研究背景
1.1.1 引言
如原論文所說,強化學習(RL)承諾僅依賴獎勵函數即可解決任何指定任務。然而,這種簡單直接的RL問題表述在實際應用中常常不可行:在復雜環境中,完全從零開始探索以學習有效策略的代價極高,因為這要求智能體在學習到良好策略之前,必須通過隨機嘗試偶然成功地完成任務
事實上,即使是人類和動物也很少完全從零開始解決新任務,而是利用以往經驗中獲得的先驗知識和技能
- 受此啟發,近期有大量研究致力于將先前的離線數據整合進在線RL探索過程中[27,38,82]。
說白了,因為獎勵函數不好設計且泛化有挑戰,故有了offline to online RL,簡稱O2O RL
O2O RL 的核心思想是:首先利用一個大型的、預先收集好的離線數據集(比如人類操作的機器人演示、其他策略的運行記錄)進行預訓練,然后在此基礎上,通過與環境的少量在線交互進行微調和提升。這就像一個學徒,先看師傅的教學視頻(離線數據),再親自動手實踐(在線交互)
但這又帶來了一系列新挑戰:離線數據的分布可能與智能體在線上應遵循的策略分布不一致,從而引入分布偏移,并且如何有效利用離線數據以獲得良好的在線探索策略也并不顯而易見
? 解決辦法之一,是如此前解讀過的熱啟動RL,即《WSRL——熱啟動的RL如何20分鐘內控制機器人:先離線RL預訓練,之后離線策略熱身(模擬離線數據保留),最后丟棄離線數據做在線RL微調》
? 解決辦法之二,是本文要介紹的Q-chunking
- 在相鄰的模仿學習(IL)領域,近年來一種廣泛使用的方法是采用動作分塊(action chunking)
與根據先前數據中的狀態觀測訓練策略預測單一動作不同,該方法是訓練策略預測一小段未來動作序列(即“動作塊”)[87,11]
舉個例子:
??傳統模仿學習:你告訴機器人「把手抬高一點」
機器人預測并執行一個抬手的原子動作
??模仿學習與動作塊:你告訴機器人「拿起桌上的杯子」
機器人可能一次性預測一個包含「伸出手臂 -> 張開手掌 -> 握住杯子 -> 抬起手臂」的動作序列,然后逐一執行
雖然動作分塊在IL中有效性的完整解釋仍然是一個未解之謎,但其有效性至少可以部分歸因于它能更好地處理離線數據中的非馬爾可夫行為
——————
什么是非馬爾可夫行為?簡單地說,就是當前動作的選擇,不僅取決于當前的狀態,還可能依賴于過去一系列動作所形成的「上下文」或「習慣」,比如在模仿學習中,人類的每一次示范并不是完美的。人們在日常操作中可能存在猶豫、等待等,比如把電池插進遙控器,有點對不準,手會頓一下
本質上為建模(例如)人類演示或不同行為混合等復雜分布提供了更強大的工具[87]
動作分塊在強化學習(RL)中尚未被廣泛采用,可能是因為在RL的背景之下,完全可觀測的馬爾可夫決策過程(MDP)中的最優策略是馬爾可夫性的[72],因此分塊可能顯得沒有必要
說白了,即理論上強化學習的最終策略只需看當前狀態就能做出最優決策(這叫“馬爾可夫性”),不存在模仿學習中的非馬爾科夫行為
- 但作者注意到,雖然一般可能希望最終獲得一個最優的馬爾可夫策略,但探索問題可以通過非馬爾可夫性和時間擴展的技能更好地解決
而動作分塊為實現這一目標提供了一種非常簡單且方便的方法
換言之,雖然最終的最優策略在完全觀測的 MDP 中是馬爾可夫的,但探索問題可以更好地通過非馬爾可夫的、時間擴展的「技能」來解決 - 此外,動作分塊還為利用離線數據提供了更優的途徑(能夠更好地處理數據中的非馬爾可夫行為),并且通過實現無偏的n步回溯『即enabling unbiased n-step backups,其中n等于分塊長度』,甚至提升了基于TD的強化學習的穩定性和效率
在強化學習中,一個關鍵環節是“回頭看”之前的決策好不好,也就是價值回溯
chunking 通過“動作分塊”的方式,一次性預測和評估多步連續動作,讓系統能整體判斷一段行為的價值,不僅回溯更快,還能避免傳統多步方法中常見的估值偏差
因此,結合對離線數據的預訓練,動作分塊為緩解強化學習中的探索難題提供了一種極具吸引力且非常簡單的方式
對此,來自UC伯克利的研究者提出了帶有動作分塊的Q學習(簡稱Q-chunking),這是一種在離線到在線強化學習(RL)環境中改進通用時序差分(TD)型actor-critic RL算法的方法『即a recipe for improving genericTD-based actor-critic RL algorithms in the offline-to-online RL setting』
詳見見下圖圖1
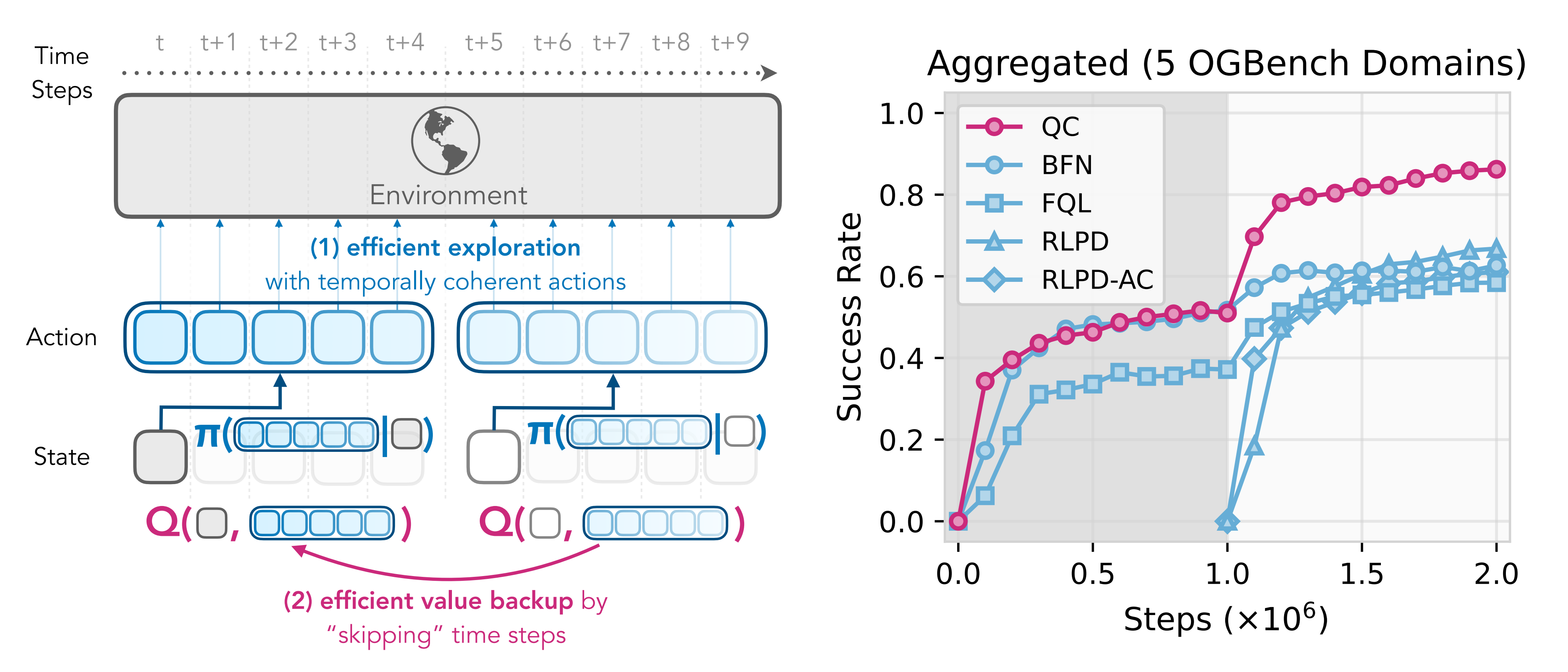
其核心思想是在動作序列層面運行強化學習
- 策略預測未來h步的動作序列,并以開環方式逐步執行這些動作
- 評估器(critic)接收當前狀態和一個動作序列,并估算執行整個動作序列的價值,而不是單獨的某個動作
在這個擴展動作空間上運行強化學習有兩個主要好處:
1?通過將策略正則化到表現出時間連貫性的先驗行為數據上,可以優化策略以生成時序一致的動作
2?用標準TD回傳損失訓練的評估器實際上是在執行n步回傳,并且沒有通常出現在樸素n步回報方法中的離策略偏差,因為評估器考慮了完整的動作序列
1.1.2 相關工作
第一,對于離線到在線強化學習方法
側重于利用先前的離線數據來加速在線強化學習[85,69,36,1,86,88,7,49,89,38]
- 最簡單的離線到在線強化學習方法是,首先使用現有的離線強化學習算法在離線數據上進行預訓練,然后繼續采用相同的離線優化目標,在不斷擴展的數據集上進行在線訓練,結合了原始離線數據和重放緩沖區數據 [48,35,32,74,56,2,41,36]
雖然這種樸素的方法實現簡單,但通常會導致過于悲觀的估計,從而抑制探索,進而影響在線采樣效率。已有多項研究嘗試通過在線調整悲觀程度來解決這一問題 [89,49,41,36,79] - 然而,這些方法往往難以調優,并且在在線采樣效率方面,有時仍不及一個簡單且正則化良好的在線強化學習算法,即從頭開始同時學習離線數據和在線重放緩沖區數據 [7-Efficient online reinforcementlearning with offline data]
Q-chunking的方法通過價值回傳加速和時間一致性的探索,進一步提升了離線到在線強化學習方法的樣本效率
第二,對于動作分塊(action chunking)
其是一種由機器人學家在模仿學習(IL)領域推廣的技術,該方法讓策略以開環方式預測并執行一系列動作(即“動作塊”)[82]
- 研究表明,動作分塊能夠提升策略的魯棒性[87,22,8],并能處理離線數據中的非馬爾可夫行為[87]
現有結合動作分塊的強化學習(RL)方法通常側重于對通過模仿學習預訓練的策略進行微調[59]——即有的先模仿學習做預訓練,然后RL做微調 - Tian等人[75]提出,通過將n步回報與Transformer結合,學習基于動作塊的評價器(critic)。然而,他們的方法僅將分塊應用于評價器,而仍然優化單步行動者(actor)
Li等人[37]同樣觀察到,在短動作塊上學習評價器可以消除n步回報備份中的離策略偏差,從而實現更穩定和高效的價值學習
不過該的工作與Q-chunking的工作存在關鍵差異——Li等人[37]在在線分幕RL場景下進行操作[81,30],并采用高斯策略預測運動基元(Motion Primitives, MP)[61,52]的參數,這些參數隨后在每個回合開始時用于生成完整的動作序列
傳統的RL中,策略通常被建模為高斯分布,即在給定狀態下,動作服從某個均值和方差的高斯分布。這種簡單模型難以捕捉離線數據中復雜的、多模態的、非馬爾可夫的行為模式
所以,也就有了如果僅僅將動作塊引入傳統的 RLPD 算法,但策略仍使用高斯分布(RLPD-AC),但如圖2所示,作者發現高斯策略效果不佳,比如其性能遠低于不使用動作塊的原始 RLPD
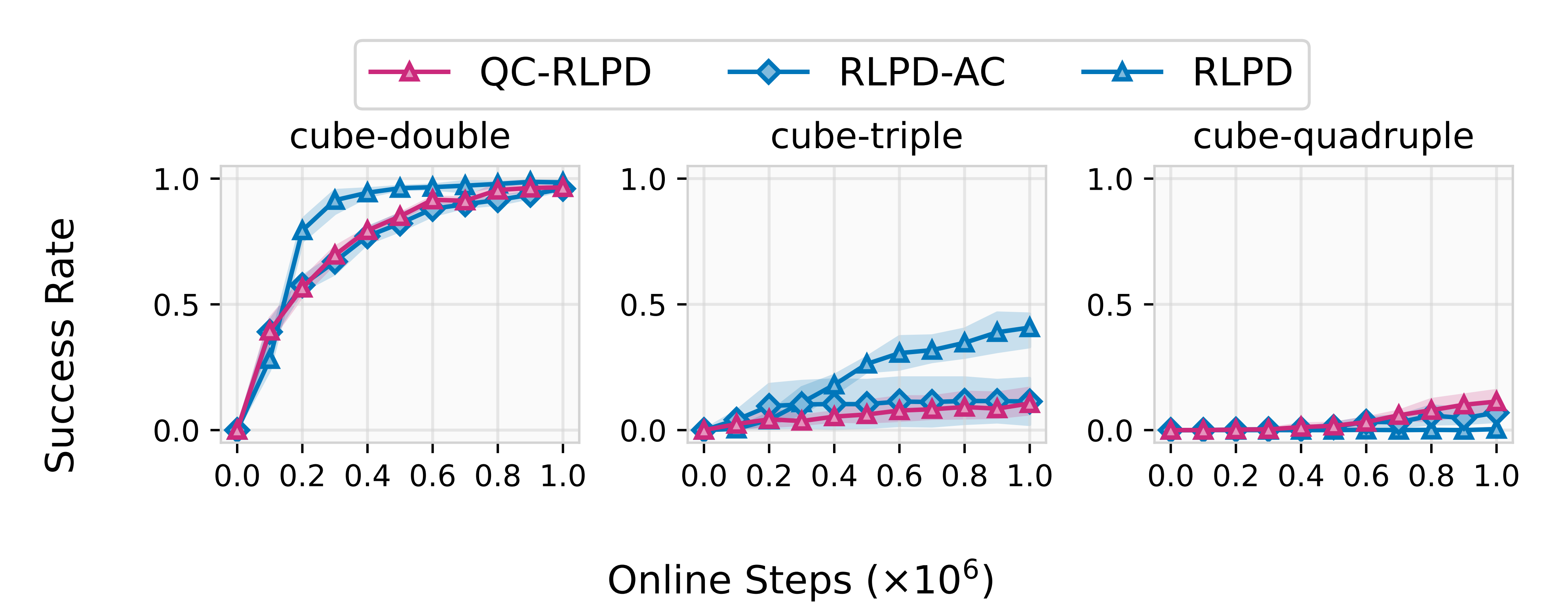
(1) RLPD在離線數據和在線回放緩沖區上運行在線強化學習 [7]
(2) RLPD-AC與RLPD為同一算法,但在時間擴展的動作空間中運行(動作塊大小為5)
(3) QC-RLPD在actor上額外采用行為克隆損失(4個種子)
相比之下,Q-chunking在傳統的離線到在線RL設置中工作,并利用更具表達能力的基于流匹配(flow-matching)的策略,直接在原始動作空間中預測短動作序列
下文1.2.3 節會詳解 - Seo和Abbeel[63]同樣在動作塊上訓練評價器,并施加行為克隆損失,這與Q-chunking背后的原理一致
與Q-chunking的工作的關鍵區別在于,他們采用了多層次、因式分解的評價器架構[64],通過迭代離散化從粗到細生成并細化動作塊
在每一層,動作空間被離散化為若干區間,Q函數針對每個動作維度和時間步獨立建模,條件為上一粗層級預測的整個動作塊
雖然這種因式分解的評價器設計使得價值最大化的動作采樣變得可行,但它對動作空間施加了較強的結構性假設,限制了每個細化層級的策略表達能力
相比之下,Q-chunking的方法不做此類假設,使得能夠推導出兩種通用算法,其中評價器和策略均可直接作用于動作塊,無需因式分解或迭代離散化/細化
第三,對于采用時序一致的動作進行探索
- 現有方法
要么依賴于通過啟發式構建的時序相關動作噪聲[39]
要么采用分層結構的策略(詳見下文)
但這種方法在在線訓練過程中往往難以穩定
或者使用預訓練且凍結的技能策略[58,82],這類方法不便于進行細粒度的在線微調 - 本文的方法使用單一網絡來表示策略,生成具有時序延展性的動作片段,并通過一個易于優化且穩定的目標函數進行訓練
此外,Q-chunking的方法不包含任何凍結或預訓練的組件,從而保證了在線微調的靈活性
第四,分層強化學習與選項框架
關于學習時間延展動作的研究也在分層強化學習(HRL)文獻中得到了廣泛關注[14,16,77,13,34,78,57,60,47,3,65,58,21,84]
- HRL方法通常訓練一組能夠直接與環境交互的低層策略,并配合一個高層策略來選擇這些低層策略。低層策略可以是手工設計的[12],也可以通過在線方式自動發現[16,34,77,78,47],或者利用離線技能發現方法進行預訓練[52,45,65,3,68,58,76,50,27,19,9,55]
- 選項框架則提供了一種更為復雜且功能更強大的形式化方法,其中低層策略還與可學習的啟動條件和終止條件相關聯,使低層策略的使用更加靈活[73,44,10,43,66,67,31,13,70,51,18,4,29,5,6,15]
- HRL領域長期存在的挑戰在于其雙層優化問題:在訓練過程中同時更新低層和高層策略時,高層策略必須針對不斷變化的目標函數進行優化,這可能導致不穩定性[47]
為了解決這一問題,一些方法會在初步預訓練后凍結低層策略[3,58,82],以提升在線訓練過程中的穩定性
本文的方法是HRL的一個特例,其中低層技能以開環方式執行一系列動作。這一設計選擇使得作者能夠將雙層優化問題簡化為在時間延展動作空間中的標準強化學習目標,同時保留了許多HRL方法相關的探索優勢
第五,多步潛在空間規劃與搜索
- 這是一種常見于基于模型的強化學習方法的技術,這些方法利用學習得到的模型來優化短期動作序列,以獲得高回報的軌跡 [51,62]。這些方法通過在編碼后的潛在空間上訓練動力學模型實現,其中模型接收一個潛在狀態和一個動作,預測下一個潛在狀態及其對應的獎勵值。
該潛在動力學模型與潛在狀態上的價值網絡結合后,能夠通過在潛在動力學模型中簡單地模擬動作序列,為任意給定的潛在狀態出發的動作序列即時提供 Q 值的估計 - 相比之下,Q-chunking并不學習潛在動力學模型,而是直接訓練一個 Q 網絡來估算動作序列的價值
最后,這些方法主要應用于純在線強化學習場景,而Q-chunking則關注從離線到在線的強化學習設定
1.1.3 研究背景:離線到在線RL、時序差分與多步回報
首先,對于離線到在線強化學習
在本文中,作者考慮一個無限時域、完全可觀測的馬爾可夫決策過程(MDP)
其中
是狀態空間
是動作空間
是轉移核
是獎勵函數
是初始狀態分布
是折扣因子
- 且還假設存在一個先驗的離線數據集D 由來自
的轉移軌跡
組成
離線到在線強化學習的目標是找到一個策略,使得期望折扣累計獎勵(或折扣回報)最大化:
如上文提到過的,離線到在線強化學習算法分為兩個不同的階段:
- 離線階段,在離線數據D 上對策略進行預訓練
- 在線階段,通過與環境的交互進一步微調策略
其次,對于時序差分與多步回報
基于時序差分(TD)的強化學習算法通常通過使用時序差分(TD)損失函數[72],學習,以近似從狀態 s 和動作 a 出發時,策略能夠獲得的最大期望折扣累計回報:
其中,是對
的估計,通常選擇為
:
其中,是從某些離策略軌跡中采樣的,
是
?的一個延遲版本,為了學習的穩定性,不允許梯度通過
- 當TD 誤差被最小化時,
收斂到策略
的期望折扣值
隨著有效視野的增加,學習速度變慢,因為價值只向后傳播一步(從
到
)
- 為了加速長視野的價值回傳,一個常見的策略是采樣長度為
的軌跡片段
,并由此構造一個
步回報[80,72]——定義為公式3
其中,
該的價值估計允許價值在時間步數上傳播時實現
倍的加速。該估計器有時被稱為未修正的
步回報估計器[17,33],因為當數據收集策略與當前策略
不同時會產生偏差
盡管如此,由于n 步回報實現簡單,它已被廣泛應用于大規模RL 系統[46,25,28,83]
1.2?Q-Chunking(Q-分塊)的完整方法論
如原論文所述,接下來,會首先介紹Q-分塊的兩個主要設計原則:
- 在時間擴展的動作空間(即動作塊的空間)上進行Q學習
- 在該擴展動作空間中施加行為約束
隨后,將介紹Q-分塊(QC,QC-FQL)的實際實現方法,這些方法作為有效的基于時序差分(TD)的離線到在線強化學習算法『followed by practical implementations of Q-chunking (QC, QC-FQL) as effective TD-based offline-to-online RL algorithms』
1.2.1?在動作塊空間上的Q-Learning:加速價值傳播且可無偏估計
傳統強化學習中的 Q 函數評估的是在狀態?
?下執行單個動作?
?所能獲得的最大未來折扣獎勵,而Q-chunking的首要設計原則是在時間擴展的動作空間(即動作塊空間)上應用Q學習
與普通的基于一步時序差分(TD)的actor-critic方法不同,后者(一步時序差分TD)訓練的是Q函數和策略
而Q-chunking的方法則用一連串的 h 個連續動作來同時訓練critic 和actor
即we instead train both the critic and the actor with a span of h consecutive actions
在實際操作中,這包括對批量的轉移數據進行評論者(critic)和行動者(actor)的更新,這些轉移數據由一個隨機狀態
、一個后續動作序列以及狀態
和未來第
步的狀態
組成
具體而言,作者通過以下時序差分(TD)損失函數來訓練
其中,且
是目標網絡參數,通常是
的指數移動平均值 [24]
上述 TD 損失與公式 3
中的 n 步回報具有顯著相似性(其中 n 等于 h)
但存在一個關鍵區別:n 步回報備份中使用的 Q 函數僅接收一個動作(在時間步t),而Q-chunking的 Q 函數則接收整個動作序列
這個區別的意義可以通過分別寫出標準 1 步 TD、n 步回報和 Q-chunking 的 TD 備份方程來更好地解釋
- 對于標準的1步時序差分(TD)方法,每次回傳僅將價值向前傳播一步
它將當前狀態 - 動作對的 Q 值更新為即時獎勵??加上下一狀態 - 動作對的折扣 Q 值。每次更新,價值信息只回溯一步。對于長周期任務,這意味著價值信號需要很長時間才能從最終獎勵傳播回來,學習速度很慢
- n步回報(n-step return),可以將價值以
倍的速度向前傳播,相當于將?
?時刻的 Q 值更新為:未來?
?步的實際獎勵總和,加上第?
?步后的折扣 Q 值。這樣,每次更新能將價值信息回溯?
?步,理論上能加速學習
但當區間和
為離策略(off-policy)時,可能會出現有偏的價值估計問題[17],這是因為數據集或回放緩沖區中
步獎勵
的折扣和,不再是當前策略
下期望
步獎勵的無偏估計
啥意思呢,這里存在一個關鍵問題:偏差(Bias)
? 如果用于計算 TD 目標的數據(從離線數據集或回放緩沖區中采樣)是由一個行為策略?
?生成的,而當前學習的策略是?
? 那么前?
?步的實際獎勵?
——從 行為策略 πβ 的數據 中采樣的,并不能無偏地代表當前策略?
?會獲得的?
?步獎勵
因為??在這?
?步內可能采取與?
?不同的動作,從而導致不同的獎勵序列。這種偏差在離線RL中尤為突出
上面說了一大堆,但如果對于剛學RL的初學者來說,繞老繞去繞暈了,so,到底啥意思呢,我還是用生活中的例子來做個類比
假設你是一個學生(學習策略
),正在復習歷史考試。你手里有一份別人(行為策略πβ)整理的錯題筆記(離線數據集)
- 這份筆記記錄了別人做題時的每一步選擇(動作 a)和對應的得分(獎勵 r)
現在你想通過這份筆記快速學會“如何得高分”
n 步回報的策略是:
“我不僅看當前這一步的得分,還連續看接下來 n 步的得分,來總結規律。”- 但問題是:
別人(πβ)的解題思路可能和你()完全不同
比如別人在某一步選了“背朝代口訣”——πβ的動作,而你更傾向于“理解歷史背景”(的動作)
如果盲目用別人的后續得分來指導你,可能會誤導你——因為你們的選擇不同,后續的得分路徑也會不同。這就是偏差(Bias)的來源:
用別人的行為數據(πβ)來估算你自己的策略(π)的價值,會導致價值估計不準確
- Q-chunking價值回傳與
步回報類似,每步也將價值向前傳播h步,但不會出現這種有偏估計問題
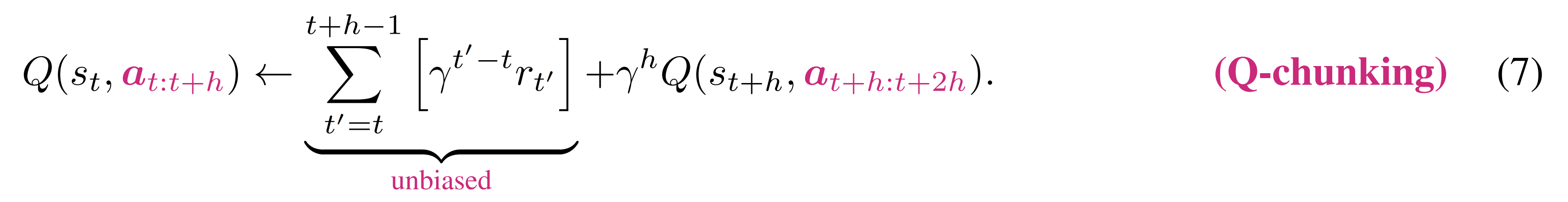
原因在于與步回報將價值回傳到1步Q函數不同,Q-chunking回傳將價值回傳到
步Q函數,該函數接收與獲得
步獎勵
時完全相同的動作,從而消除了有偏價值估計
因此,Q-chunking價值回傳在加速價值傳播的同時,能夠保持無偏的價值估計
說白了,Q函數
的輸入就是整個動作塊
,而TD目標中的獎勵求和項
,正是執行這個動作塊
所獲得的實際獎勵
為什么這能消除偏差?
- 因為 Q 函數評估的就是「在?
?狀態下,如果執行了?
?這個特定序列,能得到多少價值?」
- 右邊的獎勵項
,也正是這個特定序列所產生的實際獎勵
這就好比,你問「如果我按照這個菜譜做菜,會得到什么味道?」,然后你實際按照菜譜做了,嘗到了味道。這個味道就是無偏的,因為它就是「這個菜譜」的結果
1.2.2?時序一致性探索的行為約束:解決動作不一致(利用離線數據中具有時序連貫性的動作序列)
Q-chunking 的第二個設計原則通過在 的目標中引入行為約束,解決了動作不一致性問題——定義為公式8:
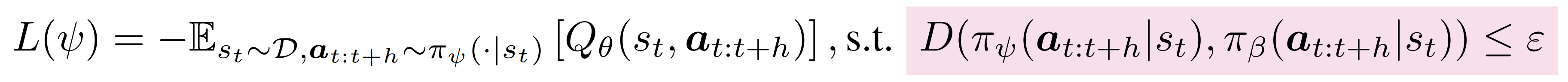
其中,將表示為離線數據
中的行為分布,
表示某種距離度量,用于衡量學習到的策略
與
偏離程度
直觀來看,對時序擴展動作序列施加行為約束,使得能夠利用離線數據集中具有時序連貫性的動作序列
- 這在時序擴展動作空間中尤其具有優勢,相較于原始動作空間,因為離線數據通常呈現非馬爾可夫結構『例如,來自腳本化策略[54]、人工遠程操作員[42]或用于子任務的噪聲專家策略[54,20]』,而這些結構無法被馬爾可夫行為約束很好地捕捉
時序連貫的動作對于在線探索來說是理想的,因為它們類似于時序擴展的技能(如在導航中朝某一方向移動、越障動作等),有助于以結構化的方式穿越環境,而不是使用隨機動作——隨機動作往往導致數據局限于初始狀態附近
說白了,離線數據,特別是人類演示,天然就包含這種時間連貫的、有目的性的行為。例如,人類操作機器人時,不會隨意地移動一個關節,而是會執行「伸手」、「抓取」、「移動」等一系列結構化的動作。Q-chunking 的目標就是利用這些「人類智慧」來指導智能體的在線探索 - 對動作分塊策略施加行為約束,是一種非常簡單的方法,可以近似地提取技能,而無需像基于技能的方法那樣訓練具有雙層結構的策略
實際上,作者確實觀察到,帶有此類行為約束的Q分塊能夠通過時序一致性的動作與環境交互和探索,從而緩解了強化學習中的探索難題
1.2.3 實際實現:QC與QC-FQL
Q-chunking 的一個關鍵實現難點在于,如何在動作序列層面施加能夠體現非馬爾可夫行為的良好行為約束。實施良好行為約束的前提之一,是策略能夠捕捉復雜的行為分布(例如,通過流模型/擴散策略)
- 首先,而如上文提到過的,高斯策略作為在線強化學習算法中的默認選擇,并不足以滿足這一需求。實際上,如果直接采用現成的在線算法(例如 RLPD[7]),并結合行為克隆損失應用 Q-chunking,通常會發現其表現較差,即如上文出現過的圖2
- 其次,如此文所說,流匹配是一種生成模型,它的思想是學習一個連續的動力學過程(continuous dynamics),將一個簡單的初始分布(例如標準高斯噪聲)平滑地轉化為任意復雜的目標數據分布
你可以把它想象成:你有一團泥巴(高斯噪聲),流匹配就是學習一套「雕刻路徑」,能把這團泥巴精準地雕刻成任何你想要的形狀(復雜的動作塊分布)
通過流匹配訓練的行為策略,能夠:
? 捕捉復雜分布:在高維動作塊空間中建模多模態、非馬爾可夫的復雜行為分布
? 生成高質量樣本:從噪聲中生成與離線數據中觀察到的行為模式高度相似的、時間連貫的動作塊
為了施加良好的行為約束,作者首先使用flow-matching 目標[40] 來訓練一個行為克隆流策略,以捕捉行為分布
該流策略由一個狀態條件下的速度場預測模型 參數化,作者用
表示流策略參數化的動作分布,它作為離線數據中真實行為分布的近似(
)
有了這個強大的行為策略?,Q-chunking 提出了兩種實用的實現方案,一個是QC,一個是QC-FQL
1.2.3.1 QC:即帶有隱式KL行為約束的Q-chunking
簡言之,QC(Q-chunking with Implicit KL Behavior Constraint) 不顯式地訓練一個獨立的策略網絡來最大化 Q 值,而是通過 Best-of-N 采樣 的方法來實現策略優化和行為約束的結合
還是說的再直白點吧
- 它首先訓練一個特殊的“流策略”(flow policy)來掌握離線數據中復雜的、多步驟的行為
- 然后,在在線學習時,它利用這個策略生成若干個候選的“動作塊”(比如,生成 16 個)
- 接著,它用其價值函數(Q - function)從這些候選項中選出最好的一個并執行。這種“N 選最優”的采樣方式,巧妙地讓智能體的行為不會偏離從數據中學到的有效策略太遠
如公號具身紀元所說,這個設計的目的是不希望 AI 的行為和人類演示偏差太大,但又不想“死盯著人類的動作照抄”,而是希望它“以人為參考,自主發揮”
就像你讓 AI 學炒菜,給它一個人類炒菜的 10 段視頻,它每次從中“學一段”,但不是照抄,而是從中挑一段看起來最香的學。這種挑選方式既靠近人類風格,又保留優化空間
具體而言,作者通過學習到的行為分布對他們的策略施加KL約束——定義為公式9:
雖然可以將KL作為損失函數的一部分,但對于流模型來說,估算KL散度或對數概率在實際操作中具有挑戰性
因此,作者采用best-of-N采樣方法[71],在最大化Q值的同時,整體上隱式施加KL約束
- 具體來說,這包括首先從學習到的行為策略
中——即預訓練好的流匹配行為策略,采樣N個動作分塊
- 然后選擇能夠最大化時序擴展Q函數的動作塊樣本:
已有研究表明,最佳N采樣對原始分布的KL散度存在一個閉式上界 [26]:
這在一定程度上隱式滿足了KL約束(見公式9)。直接調整N的取值對應于約束強度的變化
由于作者使用best-of-N 采樣來近似策略優化(公式8)
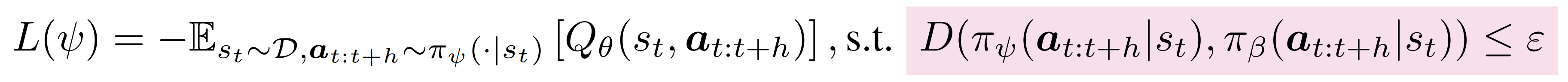
作者可以完全避免單獨對策略進行參數化,只需從行為策略
中采樣即可
具體來說,作者使用best-of-N采樣來生成動作,用于(1)與環境交互,以及(2)在TD 回傳中提供動作樣本,遵循Ghasemipour 等人[23] 的方法
因此,他們的算法只需一個額外的損失函數:
其中,
雖然QC方法簡單且易于實現,但確實會帶來一些額外的計算開銷(采樣N×)。故作者又提出了該方法的一個變體,該變體利用了更為廉價的現成離線/離線到在線強化學習方法FQL[56]
1.3.1.2?QC-FQL:帶有2-Wasserstein距離行為約束的Q-chunking
簡言之,這是隱式 KL 約束一個計算成本稍低的變體。它不采用“N 選最優”采樣,而是訓練一個獨立的策略網絡,并通過正則化使其行為與“流策略”保持接近。這用另一種方式達到了同樣的目標,即在優化獎勵的同時,充分利用離線數據
如果說 QC 是“從人類動作中挑最好的”,那 QC - FQL 更像是“你自己創造動作,但每次都檢查:這段動作離人類動作有多遠?太遠了就拉回來一點”
// 待更





MySQL學習筆記(完):事務和鎖)










模式 透明裝飾模式與半透明裝飾模式)


復現與原理分析)