深度學習自然語言處理(RNN) day

1.?感知機與神經網絡

1.1?感知機

????????生物神經元：

1.1.1?感知機的概念

????????感知機（Perceptron），又稱神經元（Neuron，對生物神經元進行了模仿）是神經網絡（深度學習）的起源算法，1958年由康奈爾大學心理學教授弗蘭克·羅森布拉特（Frank Rosenblatt）提出，它可以接收多個輸入信號，產生一個輸出信號。

????????神經元更通用的圖形表示和表達式：

1.2.1?感知機的功能

????????作為分類器/回歸器，實現自我學習：

????????實現邏輯運算，包括邏輯和（AND）、邏輯或（OR）：

1.3.1?感知機的缺陷

????????多層感知機：

1.2?神經網絡

1.2.1?什么是神經網絡

????????感知機由于結構簡單，完成的功能十分有限。可以將若干個感知機連在一起，形成一個級聯網絡結構，這個結構稱為“多層前饋神經網絡”（Multi-layer ?Feedforward Neural Networks）。所謂“前饋”是指將前一層的輸出作為后一層的輸入的邏輯結構。每一層神經元僅與下一層的神經元全連接。但在同一層之內，神經元彼此不連接，而且跨層之間的神經元，彼此也不相連。

1.2.2?神經網絡的功能

????????1989年，奧地利學者庫爾特·霍尼克（Kurt Hornik）等人發表論文證明，對于任意復雜度的連續波萊爾可測函數（Borel Measurable Function）f，僅僅需要一個隱含層，只要這個隱含層包括足夠多的神經元，前饋神經網絡使用擠壓函數（Squashing Function）作為激活函數，就可以以任意精度來近似模擬f。如果想增加f的近似精度，單純依靠增加神經元的數目即可實現。

????????這個定理也被稱為通用近似定理（Universal Approximation Theorem），該定理表明，前饋神經網在理論上可近似解決任何問題。

????????通用近似定理：

????????其實，神經網絡的結構還有另外一個“進化”方向，那就是朝著“縱深”方向發展，也就是說，減少單層的神經元數量，而增加神經網絡的層數，也就是“深”而“瘦”的網絡模型。
????????微軟研究院的科研人員就以上兩類網絡性能展開了實驗，實驗結果表明：增加網絡的層數會顯著提升神經網絡系統的學習性能。

????????多層神經網絡計算公式：

????????以下是一個多層神經網絡及其計算公式：

1.3?MLP

????????"MLP"通常指的是"多層感知器"（Multilayer Perceptron），是一種最基本的人工神經網絡模型之一。它由多個神經元層組成，每個神經元層與下一層全連接。MLP通常由一個輸入層、一個或多個隱藏層以及一個輸出層組成。

????????- 輸入層（Input Layer）：接收原始數據輸入的層。
????????- 隱藏層（Hidden Layers）：對輸入數據進行非線性變換的層。這些層的存在使得MLP可以學習非線性關系。
????????- 輸出層（Output Layer）：產生最終預測結果的層。根據問題的不同，輸出層可以具有不同的激活函數，比如用于二分類問題的sigmoid函數，用于多分類問題的softmax函數，或用于回歸問題的線性激活函數。
????????MLP通過反向傳播算法進行訓練，利用梯度下降等優化算法來最小化預測值與真實標簽之間的誤差。它在許多領域都得到了廣泛的應用，如圖像識別、自然語言處理、預測分析等。

????????MLP和感知器模型效果對比：

1.3.1 MLP的pytorch實現：

????????- 先寫出MLP的模型；
????????- 對模型進行實例化；
????????- 用隨機輸入測試MLP。

import torch
import torch.nn as nn
import torch.nn.functional as Fx_input = torch.randn(2, 3, 10)
# print(x_input)class MLP(nn.Module):def __init__(self, input_dim, hidden_dim, output_dim):super(MLP, self).__init__()self.fc1 = nn.Linear(input_dim, hidden_dim)self.fc2 = nn.Linear(hidden_dim, output_dim)def forward(self, inputs):intermediate = F.relu(self.fc1(inputs))outputs = self.fc2(intermediate)outputs = F.softmax(outputs, dim=2)return outputsmodel = MLP(10, 20, 5)
x_output = model(x_input)
print(x_output)

1.4?DNN模型

????????DNN（Deep Neural Network，深度神經網絡）是一類人工神經網絡，其特點是包含多個隱藏層。與傳統的淺層神經網絡（如只有一個隱藏層的多層感知器MLP）相比，DNN通過增加隱藏層的數量，可以學習和表示數據中更加復雜和抽象的特征。

????????關鍵特點：

深度：DNN的“深度”指的是網絡中隱藏層的數量。一個網絡層數越多，其能夠捕捉的特征越復雜。
層次化特征表示：DNN通過逐層抽象和變換數據，逐步提取低級、中級和高級特征。例如，在圖像識別任務中，前幾層可能提取邊緣和紋理，中間幾層可能提取局部形狀和圖案，后幾層則可能提取整體的物體結構和類別信息。
非線性變換：每個隱藏層通常由線性變換和非線性激活函數組成。這些非線性激活函數（如ReLU、sigmoid、tanh等）使得DNN可以學習非線性映射。

????????組成部分：

輸入層：接收原始數據輸入。
隱藏層：包括多個隱藏層，每個層包含若干個神經元，這些神經元通過線性變換和非線性激活函數處理輸入數據。
輸出層：生成最終的預測結果。輸出層的形式和激活函數取決于具體任務（如分類或回歸）。

????????DNN網絡可以表示為： $S=f(\mathbf{W}_{in}X+b)$ ；其中 S表示網絡的輸出，X是輸入數據，{W}_{in} 是輸入層到隱藏層的權重參數，b 是偏置項，f是激活函數。

1.4.1?訓練過程

????????DNN的訓練過程通常使用反向傳播（backpropagation）算法和優化算法（如梯度下降、Adam等）。反向傳播算法通過計算每個參數的梯度來最小化損失函數，從而調整網絡的權重和偏置。

1.4.2?DNN存在的問題

????????傳統的深度神經網絡（DNN）在處理時序數據時存在一些問題，主要是由于其結構的固有限制而無法捕捉前置時間的信息。為了解決這個問題，可以通過在網絡中引入新的參數和結構來處理時序數據。

????????傳統MLP形如上圖，通過不斷學習，調節Win和Wout，從而適應任務。
????????在傳統的多層感知器（MLP）中引入時間特征，并通過堆疊的方式傳遞前置時間的信息。這樣的結構就引入了新的參數Ws，并且利用這些參數來調節前置時間信息的傳遞。同時，為了簡化計算，所有的時間權重參數都可以使用同一個參數矩陣Ws。
????????通過這樣的修改，網絡在每次更新中都包含了上一時刻的狀態 {S}_{t-1} 和權重參數 Ws，從而能夠更好地捕捉時序數據中的前置時間信息。這種方法有效地擴展了傳統DNN網絡的應用范圍，使其能夠處理更復雜的時序數據任務，例如時間序列預測、語音識別等。

????????具體而言，傳統的DNN網絡可以表示為： $S=f(\mathbf{W}_{in}X+b)$ ；其中S表示網絡的輸出，X是輸入數據，Ws 是輸入層到隱藏層的權重參數，b 是偏置項，f是激活函數。

????????在引入時間特征之后，網絡的更新規則可以修改為： $S_t=f(\mathbf{W}_{in}X+\mathbf{W}_{s}S_{t-1}+b)$ ；其中 $S_t$ 表示在時間 t的輸出， $S_{t-1}$ 表示前一時刻的狀態，Ws 是用來傳遞前置時間信息的權重參數。
????????這樣就可以看到，在每次更新中，都包含了上一時刻的狀態 $S_{t-1}$ 和權重參數Ws

2.?RNN 模型

2.1?先導

2.1.1?為什么需要循環神經網絡 RNN

????????上圖是一幅全連接神經網絡圖，我們可以看到輸入層-隱藏層-輸出層，他們每一層之間是相互獨立地，(框框里面代表同一層)，每一次輸入生成一個節點，同一層中每個節點之間又相互獨立的話，那么我們每一次的輸入其實跟前面的輸入是沒有關系地。這樣在某一些任務中便不能很好的處理序列信息。

2.1.2?時序數據

????????對于不同類型的數據和任務，理解數據的順序和前后關系的重要性是至關重要的。對于圖像識別這樣的任務來說，圖片的前后順序并不會影響識別結果，因為圖片中的像素是獨立且無序的。但是，當涉及到文本、股票、天氣、語音等具有時間順序或邏輯順序的數據時，順序的變化會對結果產生顯著影響。

????????舉例來說，對于一句話"我吃蘋果"，如果改變順序為"蘋果吃我"，意思完全變了。這種語言的表達方式對順序和詞語的關聯有著極高的敏感性。而對于股票和天氣數據，先后順序也具有重要意義，因為后續的數據可能受到之前數據的影響，如股票市場的走勢或天氣的變化趨勢。
????????在文本理解方面，順序也至關重要。例如，對于經典的古詩"床前明月光，疑是地上霜。舉頭望明月，低頭思故鄉。"，如果改變了詩句的順序，那么整首詩的意境和情感也將隨之改變，這就是所謂的"蝴蝶效應"。一個微小的改變可能會導致整體結果的巨大變化。
????????因此，在處理具有時間或邏輯順序的數據時，我們必須考慮到順序的重要性，并設計相應的模型來充分利用數據的前后關系，以獲得更準確和有意義的結果。這也是循環神經網絡（RNN）等模型在這些任務中被廣泛使用的原因之一，因為它們能夠捕捉到數據的順序信息，并根據前面的輸入來預測后續的輸出。

2.2?RNN 原理

2.2.1?概述

????????循環神經網絡（Recurrent Neural Network，RNN）是一種神經網絡結構，專門用于處理序列數據。與傳統的前饋神經網絡不同，RNN 在內部具有反饋連接，允許信息在網絡內部傳遞。這種結構使得 RNN 能夠對序列數據的歷史信息進行建模，并在一定程度上具有記憶能力。
????????在自然語言處理領域，RNN 被廣泛應用于語言建模、機器翻譯、情感分析等任務。通過捕捉單詞之間的上下文信息，RNN 能夠更好地理解語言的含義和結構。
????????同時，RNN 也在時間序列預測領域發揮著重要作用，比如股票價格預測、天氣預測等。通過學習序列數據的模式和趨勢，RNN 能夠提供有用的預測信息，幫助人們做出決策。
????????然而，傳統的 RNN 存在一些問題，例如難以處理長期依賴關系、梯度消失或梯度爆炸等。為了解決這些問題，出現了一些改進的 RNN 變種，如長短期記憶網絡（LSTM）和門控循環單元（GRU）。這些變種結構能夠更有效地捕捉長期依賴關系，并且在訓練過程中更加穩定。

2.2.2?模型架構

????????循環神經網絡（RNN）是深度學習中的一種架構，專門設計來處理序列數據，例如時間序列數據或自然語言文本。RNN的核心特征在于它能夠在處理序列的每個元素時保留一個內部狀態（記憶），這個內部狀態能夠捕捉到之前元素的信息。這種設計使得RNN特別適合處理那些當前輸出依賴于之前信息的任務。

????????常見的RNN架構如下圖兩種：

????????左圖可以理解為，先將每一層的網絡簡化，再將網絡旋轉90度得到的簡化圖，而右邊兩種類型，可以理解為，再將左圖繼續進行簡化。
????????在RNN的經典架構中，網絡通過一個特殊的循環結構將信息從一個處理步驟傳遞到下一個。這個循環結構通常被稱為“隱藏層狀態”或簡單地稱為“隱藏狀態”。隱藏狀態是RNN的記憶部分，它能夠捕獲并存儲關于已處理序列元素的信息。

????????當RNN處理一個序列時，它會在每個時間步接受一個輸入，并更新其隱藏狀態。這個更新過程依賴于當前的輸入和之前的隱藏狀態，從而使得網絡能夠“記住”并利用過去的信息。這個過程可以通過以下數學公式簡化表達： $s_t=f(\mathbf{U}·x_t+\mathbf{W}·s_{t-1})$ ；在這個公式中， ${S}_{t}$ 表示在時間步t的隱藏狀態， ${x}_{t}$ 是當前時間步的輸入，U 和 W分別是輸入到隱藏狀態和隱藏狀態到隱藏狀態的權重矩陣。函數f通常是一個非線性函數，如tanh或ReLU，用于引入非線性特性并幫助網絡學習復雜的模式。

????????RNN的輸出在每個時間步也可以計算出來，這依賴于當前的隱藏狀態： ${O}_{t} = g(V{s}_{t})$ ；其中 ${O}_{t}$ 是時間步t的輸出，V是從隱藏狀態到輸出層的權重矩陣，g是另一個非線性函數，常用于輸出層。

????????RNN也是傳統的神經網絡架構，但是他里面包含了一個“盒子”，這個盒子里記錄了輸入時網絡的狀態，在下一次輸入時，必須要考慮“盒子”。隨著不斷的輸入，盒子里也會更新，那么這個盒子就是“隱藏態”。

????????假設為一個包含三個單詞的句子，將模型展開，即為一個三層的網絡結構，可以理解為， ${x}_{t-1}$ 為第一個詞， ${x}_{t}$ 為第二個詞， ${x}_{t+1}$ 為第三個詞。

????????圖中參數含義：

${x}_{t}$ 表示第t步的輸入。比如 ${x}_{1}$ 為第二個詞的詞向量( ${x}_{0}$ 為第一個詞)；
${H}_{t}$ 為隱藏層的第t步的狀態，它是網絡的記憶單元。
- ${H}_{t}$ 根據當前輸入層的輸出與上一時刻隱藏層的狀態 ${H}_{t-1}$ 進行計算，如下所示。
  
  ???????????????????????? $H_t=f(\mathbf{U}·x_t+\mathbf{W}·H_{t-1})$
- 其中，U是輸入層的連接矩陣，W是上一時刻隱含層到下一時刻隱含層的權重矩陣，f(·)一般是非線性的激活函數，如tanh或ReLU。
{O}_{t}是第t步的輸出。輸出層是全連接層，即它的每個節點和隱含層的每個節點都互相連接，V是輸出層的連接矩陣，g(·)一是激活函數。
- $o_t=g(\mathbf{V}·s_t)$
- 帶入可以得到

????????通過這種逐步處理序列并在每一步更新隱藏狀態的方式，RNN能夠在其內部維持一個隨時間變化的“記憶”。這使得它能夠對之前序列元素的信息做出響應，并據此影響后續的輸出。這種特性對于諸如語言模型、文本生成、語音識別等許多序列處理任務至關重要。

2.2.3?RNN的內部結構

2.2.4?RNN模型輸入輸出關系對應模式

????????通過改變RNN的結構，即調整其輸入和輸出的數量和形式，可以讓它適應各種不同的任務。以下是幾種常見的RNN結構調整示例，以及它們各自適用的任務類型：

一對多（One-to-Many）：這種結構的RNN接受單個輸入并產生一系列輸出。這種模式常用于“看圖說話”的任務，即給定一張圖片（單個輸入），RNN生成一段描述該圖片的文本（一系列輸出）。在這種情況下，RNN的結構被調整為首先對輸入圖片進行編碼，然后根據這個編碼連續生成文本序列中的詞語。
多對一（Many-to-One）：與一對多相反，多對一的RNN結構接受一系列輸入并產生單個輸出。這種結構適用于如文本分類和情感分析等任務，其中模型需要閱讀和理解整個文本（一系列輸入），然后決定文本屬于哪個類別（單個輸出）。在圖片生成的上下文中，這種結構可以通過分析一系列的特征或指令來生成單個圖片輸出。
多對多（Many-to-Many）：這種結構的RNN既接受一系列輸入，也產生一系列輸出。這在需要輸入和輸出均為序列的任務中非常有用，例如機器翻譯，其中模型需要讀取一個語言的文本（一系列輸入），然后生成另一種語言的對應文本（一系列輸出）。另一個例子是小說生成，其中RNN可以基于給定的開頭或主題（一系列輸入），連續生成故事的后續內容（一系列輸出）。

2.3?RNN 代碼實現

????????重要參數含義：

Batch Size (批量大小):
- Batch size指的是在一次前向傳播或反向傳播過程中同時處理的樣本數量。
- 例如，在文本處理中，如果一批數據包含100個句子，那么batch size就是100。
Sequence Length (序列長度):
- Sequence length是指輸入數據中每個樣本的連續時間步（或詞、字符）的數量。
- 例如，在一個句子級別的任務中，一個句子可能包含10個單詞，那么序列長度就是10。
Input Size (輸入大小):
- Input size是指每個時間步輸入向量的特征維度。
- 在處理文本時，如果每個詞都被表示為一個固定維度的向量，那么input size就是這個詞向量的維度。
- 如在情感分析任務中，每個詞可能被嵌入為一個100維的向量，那么input size就是100。
Hidden Size (隱藏層大小):
- Hidden size是指RNN單元內部隱藏狀態（Hidden State）的維度。
- 在每個時間步，RNN都會根據當前輸入和上一時間步的隱藏狀態來計算新的隱藏狀態，新隱藏狀態的維度就是hidden size。
- 例如，如果我們設置hidden size為256，那么每個時間步產生的隱藏狀態就是一個256維的向量。
- 根據實驗和模型復雜度的要求自由選擇隱藏層大小，它并不是通過特定計算得出的數值。
- 隱藏層大小的選擇會影響到模型的學習能力和表示能力，同時也影響到模型的計算資源消耗。
- 實踐中，較小的隱藏層大小可能會限制模型的表達能力，而過大的隱藏層大小則可能導致過擬合、訓練時間增加等問題。
- 在決定隱藏層大小時，通常需要結合具體任務的特點、數據集規模、計算資源等因素進行合理選擇，并通過交叉驗證、網格搜索等方式進行超參數調優，以找到最優的隱藏層大小以及其他超參數組合。
Output Size (輸出大小):
- Output size通常與特定任務相關。
- 對于一般的RNN，每個時間步的輸出大小與hidden size相同，即輸出也是一個隱藏狀態維度的向量。
- 在分類任務中，最后一層可能通過一個全連接層映射到類別數目，這時最后一個時間步的輸出大小可能是類別數目的維度。
- 如果是多層或雙向RNN，輸出也可能經過額外的處理（如拼接、池化等），最終的輸出大小會根據具體應用需求來確定。
- 在最簡單的單向單層循環神經網絡（RNN）中，輸出大小（output size）的計算通常比較直接：如果目的是為了獲取每個時間步（time step）的隱藏狀態表示，并且不進行額外的轉換操作，那么每個時間步的輸出大小（output size）就等于您設定的隱藏層大小（hidden size）。
  ? ? ? ?例如，如果設置的隱藏層大小（hidden size）是256，那么在每個時間步，RNN的輸出也將是一個256維的向量。
  ? ? ? ?如果是在做序列到序列（Sequence-to-Sequence）的任務，比如機器翻譯，最后的時間步的隱藏狀態通常會通過一個線性層映射到目標詞匯表大小，這樣輸出大小就會是目標詞匯表的大小。
  ? ? ? ?如果在RNN之后添加了其他層（如全連接層或分類層）來進行進一步的處理，比如進行分類任務，那么輸出大小取決于這些后續層的設計。例如，如果您接下來是一個Softmax層用于做多分類，且類別數是10，則輸出大小將會是10，表示每個樣本的概率分布。

????????具體的單層單向RNN示例來說明維度變換過程：假設正在處理一個文本分類任務，每個單詞已經被嵌入為一個100維的向量，我們的序列長度（sequence length）是50（即最長句子有50個單詞），批量大小（batch size）是32（一次處理32個句子），我們設定的隱藏層大小（hidden size）是128。

輸入維度（input size）: 每個時間步（每個單詞）的輸入向量維度是100，所以整個輸入張量的維度是 (batch size, sequence length, input size)，即 (32, 50, 100)。
隱藏層計算: RNN會對每個時間步的輸入進行處理，并基于上一時間步的隱藏狀態生成當前時間步的隱藏狀態。隱藏狀態的維度由我們設定，這里是128維，所以每個時間步的隱藏狀態和輸出的維度都是 (batch size, hidden size)，即 (32, 128)。
輸出維度（output size）: 因為這里我們假設沒有在RNN后添加額外的層（例如分類層），所以每個時間步的輸出大小就等于隱藏層大小，也就是128維。但是，由于輸出是針對每一個時間步的，所以整個輸出序列的維度為 (batch size, sequence length, hidden size)，即 (32, 50, 128)。

????????如果后續需要進行分類，比如這是一個二分類問題，我們會把最后一個時間步的隱藏狀態（128維）通過一個全連接層（Dense Layer）映射到類別數目的維度，如2維，此時輸出大小將變為 (32, 2)，表示32個樣本的二維概率分布。

2.3.1?原生代碼

import numpy as np# 原始數據 一句話 3個單詞 每個2個維度
x = np.random.rand(3, 2)# RNN參數
input_size = 2
hidden_size = 3
# 詞表大小是輸出維度 6
output_size = 6# 初始化權重矩陣
# 輸入權重矩陣
Wx = np.random.rand(input_size, hidden_size)
# 隱藏權重矩陣
Wh = np.random.rand(hidden_size, hidden_size)
# 輸出權重矩陣
Wout = np.random.rand(hidden_size, output_size)# 偏置
bh = np.zeros((hidden_size,))
bout = np.zeros((output_size,))# 激活函數
def tanh(x):return np.tanh(x)# 初始化隱藏狀態
H_prev = np.zeros((hidden_size,))# 前向傳播
# 時間步1 第一個單詞
x1 = x[0, :]
H1 = tanh(np.dot(x1, Wx) + np.dot(H_prev, Wh) + bh)
Y = np.dot(H1, Wout) + bout# 時間步2 第二個單詞
x2 = x[1, :]
H2 = tanh(np.dot(x2, Wx) + np.dot(H1, Wh) + bh)
Y2 = np.dot(H2, Wout) + bout# 時間步3 第三個單詞
x3 = x[2, :]
H3 = tanh(np.dot(x3, Wx) + np.dot(H2, Wh) + bh)
Y3 = np.dot(H3, Wout) + bout# 輸出結果
print("時間步1的隱藏狀態:", H1)
print("時間步2的隱藏狀態:", H2)
print("時間步3的隱藏狀態:", H3)
print("時間步1的輸出結果:", Y)
print("時間步2的輸出結果:", Y2)
print("時間步3的輸出結果:", Y3)

????????np.dot 是 NumPy 庫中用于計算兩個數組的點積（dot product）的函數。它的行為取決于輸入數組的維度：

對于二維數組，np.dot 計算的是矩陣乘積。這意味著如果 A 是一個 m×n 矩陣，B 是一個 n×p 矩陣，那么 np.dot(A, B) 的結果將是一個 m×p 矩陣，其中每個元素由 A 中的行與 B 中的列之間的點積計算得出。
對于一維數組，np.dot 計算的是向量的內積（inner product）。即，如果 a 和 b 是長度相同的兩個一維數組，那么 np.dot(a, b) 就是 a 和 b 對應元素相乘之后的結果之和。
A 是一維數組（shape 為 (n,)），B 是二維數組（shape 為 (n, m)），相當于：

👉 將 A 視為一個行向量（1×n），與矩陣 B（n×m）相乘，得到一個 1×m 的結果（即 shape 為 (m,) 的一維數組）。

2.3.2?基于 RNNCell 代碼實現

import torch
from torch import nn# 創建數據 詞嵌入之后的維度
x = torch.randn(10, 6, 5)hidden_size = 8# 利用rnncell創建RNN模型
class RNN(nn.Module):def __init__(self, batch_size, hidden_size, batch_flag=True):super(RNN, self).__init__()# nn.RNNCell 返回的是隱藏層 參數 第一個維度是輸入維度（詞嵌入后的維度） 第二個是隱藏層狀態的維度self.rnncell = nn.RNNCell(input_size=5, hidden_size=hidden_size)# self.fc = nn.Linear(20, 10)self.batch_size = batch_sizeself.hidden_size = hidden_size# 標識符 類型為布爾類型self.batch_flag = batch_flag# 初始化隱藏狀態def intialize_hidden(self):self.h_prev = torch.zeros(self.batch_size, self.hidden_size)return self.h_prevdef forward(self, x, h_prev=None):"""注意傳遞進來的數據格式 一般經過詞嵌入格式（B,S,D） 但是在rnn中 需要的數據格式（S,B,D）詞數開頭:param x: 如果self.batch_flag是true就代表傳入的數據格式是（B,S,D）:return:"""if self.batch_flag:batch_size, seq_len, dim = x.size(0), x.size(1), x.size(2)# 數據處理為（S,B,D）x = x.permute(1, 0, 2)else:batch_size, seq_len, dim = x.size(0), x.size(1), x.size(2)hiddens = []if h_prev is None:init_hidden = self.intialize_hidden()else:init_hidden = h_prev# 循環遍歷每一個時間步for t in range(seq_len):# 輸入數據x_t = x[t]# 在t時刻獲取隱藏層狀態 封裝的是H1 = tanh(np.dot(x1,Wx) + np.dot(H_prev,Wh)+bh)# 初始化隱藏層狀態可以省略 init_hiddenhidden_t = self.rnncell(x_t, init_hidden)hiddens.append(hidden_t)# 所有的時間步堆疊成新的張量output = torch.stack(hiddens)# 處理數據if self.batch_flag:output = output.permute(1, 0, 2)return outputmodel = RNN(10, hidden_size)
output = model(x)
print(output.shape)

????????`nn.RNNCell` 本質上只返回隱藏狀態，它沒有單獨的輸出結果。一般在 `RNN` 中，隱藏狀態既可以被視為輸出，也可以通過一個線性層將隱藏狀態轉化為實際的輸出。

2.3.3?基于 pytorch API 代碼實現

????????官方代碼細節：https://pytorch.org/docs/stable/_modules/torch/nn/modules/rnn.html#RNN

????????官方文檔解釋：https://pytorch.org/docs/stable/generated/torch.nn.RNN.html#rnn

import torch
from torch import nn# 初始數據
x = torch.rand(10, 6, 5)# 模型參數
hidden_size = 8
batch_size = 10
sen_len = 6
input_size = 5
size_len = 20class RNNModule(nn.Module):def __init__(self, hidden_size, batch_size, input_size):super(RNNModule, self).__init__()self.hidden_size = hidden_sizeself.batch_size = batch_sizeself.input_size = input_sizeself.rnn = nn.RNN(input_size=input_size, hidden_size=hidden_size,bidirectional=True, batch_first=True)# 如果bidirectional=True，全連接層輸入需要 *2self.fc = nn.Linear(hidden_size*2, size_len)def forward(self, x):out, h_last = self.rnn(x)  # h_last得到是最后一層print(out.shape)print(h_last.shape)out = self.fc(out)return outmodel = RNNModule(hidden_size=hidden_size, batch_size=batch_size, input_size=input_size)
out = model(x)
print(out.shape)

input 是一個形狀為 (batch_size, sequence_length, input_size) 的張量，表示一批包含 T 個時間步長的序列，每個時間步長的輸入特征維度為 input_size。
h_prev 是所有序列共享的初始隱含狀態，形狀為 (batch_size, hidden_size)。
h_prev.unsqueeze(0) 將 h_prev 的批量維度增加一層，因為PyTorch RNN期望隱含狀態作為一個元組 (num_layers, batch_size, hidden_size)，在這里我們只有一個隱藏層，所以增加了一維使得形狀變為 (1, batch_size, hidden_size)。
rnn(input, h_prev.unsqueeze(0)) 執行RNN的前向傳播，得到的 rnn_output 是整個序列的輸出結果，形狀為 (batch_size, sequence_length, hidden_size)，而 state_final 是最后一個時間步的隱含狀態，形狀為 (num_layers, batch_size, hidden_size)。
兩個返回值 rnn_output 和 state_final 代表著循環神經網絡在當前時間步的輸出和最終的隱藏狀態。
- rnn_output：代表當前時間步的 RNN 輸出。對于很多序列模型而言，每個時間步都會有一個輸出。這個輸出可能會被用于下一時間步的計算，或者作為模型的最終輸出。
- state_final：代表 RNN 模型在最后一個時間步的隱藏狀態。這個隱藏狀態通常被認為是對整個序列的編碼或總結，它可能會被用于某些任務的最終預測或輸出。

1.?單向、單層RNN

? ? ? ? (1)?定義一個單層循環神經網絡（RNN）實例：

signle_rnn = nn.RNN(4, 3, 1, batch_first=True)

????????這行代碼創建了一個RNN層，其參數含義如下：

4 表示輸入序列的特征維度（feature size），即每個時間步的輸入向量長度為4。
3 表示隱藏狀態（hidden state）的維度，即RNN單元內部記憶的向量長度為3。
1 表示RNN層的數量，這里僅為單層。
batch_first=True 指定輸入張量的第一個維度代表批次(batch)，第二個維度代表時間步(sequence length)，這對于處理批次數據時更容易理解。

? ? ? ? (2)?創建輸入數據張量：

input = torch.randn(1, 2, 4)

????????這行代碼生成了一個隨機張量作為RNN的輸入，它的形狀為 (batch_size, sequence_length, feature_size)，具體到這里的值是：

1 表示批大小（batch size），即本次輸入的數據樣本數量。
2 表示序列長度（sequence length），即每個樣本的輸入序列包含兩個時間步。
4 是每個時間步輸入向量的特征維度，與RNN層設置一致。

? ? ? ? (3)?對輸入數據進行前向傳播：

output, h_n = signle_rnn(input)

????????這行代碼將之前創建的隨機輸入數據送入RNN層進行前向計算。執行后得到兩個輸出：

output 是經過RNN處理后的輸出序列，其形狀通常為 (batch_size, sequence_length, num_directions * hidden_size)。在這個例子中，因為沒有指定雙向RNN，所以 num_directions=1。因此，output 的尺寸將是 (1, 2, 3)，對應每個批次中的每個時間步輸出一個維度為3的向量。
h_n 是最后一個時間步的隱藏狀態（hidden state），它通常是最終時間步的隱藏狀態或者是所有時間步隱藏狀態的某種聚合（取決于RNN類型）。在這里，h_n 的形狀是 (num_layers * num_directions, batch_size, hidden_size)，但由于只有一層并且是無方向的RNN，所以形狀會簡化為 (1, 1, 3)，即單一隱藏狀態向量。這個隱藏狀態可以用于下個時間步的預測或者作為整個序列的編碼。

2.?雙向、單層RNN

????????雙向單層RNN（Recurrent Neural Network）是一種特殊類型的循環神經網絡，它能夠在兩個方向上處理序列數據，即正向和反向。這使得網絡在預測當前輸出時，能夠同時考慮到輸入序列中當前元素之前的信息和之后的信息。雙向單層RNN由兩個獨立的單層RNN組成，一個負責處理正向序列（從開始到結束），另一個負責處理反向序列（從結束到開始）。

????????主要特點：

雙向處理： 最顯著的特點是雙向結構，使得模型能夠同時學習到序列中某一點前后的上下文信息，這對于很多序列任務來說是非常有價值的，比如自然語言處理中的文本理解、語音識別等。
單層結構： “單層”指的是在每個方向上，網絡結構只有一層RNN，即每個方向上只有一層循環單元（如LSTM單元或GRU單元）。雖然是單層的，但由于其雙向特性，實際上每個時間點都有兩個循環單元對信息進行處理。

定義一個雙向循環神經網絡（Bi-RNN）實例：
```
bi_rnn = nn.RNN(4, 3, 1, batch_first=True, bidirectional=True)
```
這行代碼創建了一個具有雙向連接的RNN層，參數含義如下：
- 4 依然是輸入序列的特征維度（每個時間步長的輸入向量有4個元素）。
- 3 表示的是單向隱藏狀態（hidden state）的維度；由于設置了 bidirectional=True，實際上模型會同時維護正向和反向兩個隱藏狀態，因此總的隱藏狀態維度將是 2 * 3。
- 1 表示RNN層的數量，這里也是單層。
- batch_first=True 保持輸入張量的批量維度在最前面。
- bidirectional=True 指定該RNN為雙向的，這意味著對于每個時間步，除了向前傳遞的信息外，還會考慮向后傳遞的信息，從而能夠捕捉序列中前后依賴關系。
創建輸入數據張量：
```
input = torch.randn(1, 2, 4)
```
? ? ? ?這行代碼生成了一個隨機張量作為雙向RNN的輸入，其形狀仍為 (batch_size, sequence_length, feature_size)，即 (1, 2, 4)。這表示有一個樣本（batch_size=1），序列長度為2，每個時間步有4個特征。
對輸入數據進行前向傳播：
```
output, h_n = bi_rnn(input)
```
? ? 將隨機輸入數據傳入雙向RNN進行前向計算。執行后獲取的結果與單向RNN有所不同：
- output 現在包含了正向和反向兩個方向的輸出，其形狀為 (batch_size, sequence_length, num_directions * hidden_size)，在本例中為 (1, 2, 2 * 3)，即每個時間步有兩個方向上的隱藏狀態輸出拼接而成的向量。
- h_n 包含了最后時間步的正向和反向隱藏狀態，形狀為 (num_layers * num_directions, batch_size, hidden_size)，在本例中實際為 (2, 1, 3)，分別對應正向和反向隱藏狀態各一個。每個隱藏狀態向量都是相應方向上整個序列信息的匯總。

2.4?RNN的訓練方法——BPTT

????????BPTT（back-propagation through time）算法是常用的訓練RNN的方法，其實本質還是BP算法，只不過RNN處理時間序列數據，所以要基于時間反向傳播，故叫隨時間反向傳播。BPTT的中心思想和BP算法相同，沿著需要優化的參數的負梯度方向不斷尋找更優的點直至收斂。綜上所述，BPTT算法本質還是BP算法，BP算法本質還是梯度下降法，那么求各個參數的梯度便成了此算法的核心。

????????其中L是損失函數，對于多分類問題，我們使用的是多元交叉熵損失函數，也稱為分類交叉熵。

????????再次拿出這個結構圖觀察，需要尋優的參數有三個，分別是U、V、W。與BP算法不同的是，其中W和U兩個參數的尋優過程需要追溯之前的歷史數據，參數V相對簡單只需關注目前，那么我們就來先求解參數V的偏導數。

????????這個式子看起來簡單但是求解起來很容易出錯，因為其中嵌套著激活函數函數，是復合函數的求道過程。
????????RNN的損失也是會隨著時間累加的，所以不能只求t時刻的偏導。

????????W和U的偏導的求解由于需要涉及到歷史數據，其偏導求起來相對復雜，我們先假設只有三個時刻，那么在第三個時刻 L對W的偏導數為：

????????相應的，L在第三個時刻對U的偏導數為：

????????可以觀察到，在某個時刻的對W或是U的偏導數，需要追溯這個時刻之前所有時刻的信息，這還僅僅是一個時刻的偏導數，上面說過損失也是會累加的，那么整個損失函數對W和U的偏導數將會非常繁瑣。雖然如此但好在規律還是有跡可循，我們根據上面兩個式子可以寫出L在t時刻對W和U偏導數的通式：

????????整體的偏導公式就是將其按時刻再一一加起來。

2.5?RNN模型存在的問題

2.5.1?RNN中的梯度消失和爆炸

????????前面說過激活函數是嵌套在里面的，如果我們把激活函數放進去，拿出中間累乘的那部分：

????????我們會發現累乘會導致激活函數導數的累乘，進而會導致“梯度消失“和“梯度爆炸“現象的發生。至于為什么，我們先來看看sigmoid函數的函數圖和導數圖這是和tanh函數的函數圖和導數圖。

????????它們二者是何其的相似，都把輸出壓縮在了一個范圍之內。他們的導數圖像也非常相近，我們可以從中觀察到，sigmoid函數的導數范圍是(0,0.25]，tanh函數的導數范圍是(0,1]，他們的導數最大都不大于1。

????????這就會導致一個問題，在上面式子累乘的過程中，如果取sigmoid函數作為激活函數的話，那么必然是一堆小數在做乘法，結果就是越乘越小。隨著時間序列的不斷深入，小數的累乘就會導致梯度越來越小直到接近于0，這就是“梯度消失“現象。其實RNN的時間序列與深層神經網絡很像，在較為深層的神經網絡中使用sigmoid函數做激活函數也會導致反向傳播時梯度消失，梯度消失就意味消失那一層的參數再也不更新，那么那一層隱層就變成了單純的映射層，毫無意義了，所以在深層神經網絡中，有時候多加神經元數量可能會比多家深度好。

????????梯度爆炸（每天進一步一點點，N天后，你就會騰飛 ?每天墮落一點點，N天后，你就徹底完蛋）

????????之前說過我們多用tanh函數作為激活函數，那tanh函數的導數最大也才1啊，而且又不可能所有值都取到1，那相當于還是一堆小數在累乘，還是會出現“梯度消失“，那為什么還要用它做激活函數呢？原因是tanh函數相對于sigmoid函數來說梯度較大，收斂速度更快且引起梯度消失更慢。

????????還有一個原因是sigmoid函數還有一個缺點，Sigmoid函數輸出不是零中心對稱。sigmoid的輸出均大于0，這就使得輸出不是0均值，稱為偏移現象，這將導致后一層的神經元將上一層輸出的非0均值的信號作為輸入。關于原點對稱的輸入和中心對稱的輸出，網絡會收斂地更好。

????????RNN的特點本來就是能“追根溯源“利用歷史數據，現在告訴我可利用的歷史數據竟然是有限的，這就令人非常難受，解決“梯度消失“是非常必要的。解決“梯度消失“的方法主要有：
????????1、選取更好的激活函數；
????????2、改變傳播結構。

????????關于第一點，一般選用ReLU函數作為激活函數，ReLU函數的圖像為：

????????ReLU函數的左側導數為0，右側導數恒為1，這就避免了“梯度消失“的發生。但恒為1的導數容易導致“梯度爆炸“，但設定合適的閾值可以解決這個問題。還有一點就是如果左側橫為0的導數有可能導致把神經元學死，不過設置合適的步長（學習率）也可以有效避免這個問題的發生。

????????關于第二點，LSTM結構可以解決這個問題。
????????總結一下，sigmoid函數的缺點：
????????1、導數值范圍為(0,0.25]，反向傳播時會導致“梯度消失“。tanh函數導數值范圍更大，相對好一點。
????????2、sigmoid函數不是0中心對稱，tanh函數是，可以使網絡收斂的更好。

2.5.2?遠距離依賴

????????循環神經網絡（RNN）是自然語言處理和其他序列數據任務中廣泛使用的一種神經網絡架構，它通過在網絡中引入循環來處理序列數據，使得網絡能夠保持一定程度的序列信息。RNN的設計讓它在處理如文本和語音等順序數據時表現出色，因為它能夠在每個時間步上接收輸入，并保持一個內部狀態，該狀態包含了之前時間步的信息。

????????然而，RNN在處理長序列數據時面臨一個重大挑戰，即長期依賴性問題。長期依賴問題指的是當序列非常長時，RNN難以學習并保持序列早期時間步的信息。這是因為在RNN的訓練過程中，使用反向傳播算法進行梯度更新時，梯度往往會隨著傳播到更早的層而指數級衰減（梯度消失）或者指數級增長（梯度爆炸）。這導致了序列中較早時間步的信息對模型輸出的影響變得微乎其微，從而使得模型難以學習到這些信息對序列后續部分的影響。

????????以一個具體的例子來說明，假設有一個敘述故事的序列：

????????“張三昨天下午本想去運動，但突然接到公司的急事，需要他緊急處理，隨后他處理完去______________”。

????????在這個例子中，填空處的詞與序列中較早出現的“運動”一詞之間存在關聯。然而，如果使用標準的RNN來預測空白處的詞，由于長序列中的長期依賴問題，RNN可能無法有效地捕捉到“運動”這一關鍵信息，導致預測結果不準確。

????????長期依賴問題是RNN架構的一個根本性缺陷，它限制了RNN在處理具有重要長期依賴關系的長序列任務中的效能。因此，雖然RNN在處理較短序列時表現良好，但在涉及長距離時間依賴的復雜任務中，RNN的性能會大幅下降。

3.?LSTM 模型

3.1?LSTM概述

????????長短期記憶網絡（Long Short-Term Memory，LSTM）是一種特別設計來解決長期依賴問題的循環神經網絡（RNN）架構。在處理序列數據，特別是長序列數據時，LSTM展現出其獨特的優勢，能夠有效地捕捉和記憶序列中的長期依賴性。這一能力使得LSTM在眾多領域，如自然語言處理、語音識別、時間序列預測等任務中，成為了一個強大且廣泛使用的工具。

????????LSTM的核心思想是引入了稱為“細胞狀態”（cell state）的概念，該狀態可以在時間步長中被動態地添加或刪除信息。LSTM單元由三個關鍵的門控機制組成，通過這些門控機制，LSTM可以在處理長序列數據時更有效地學習長期依賴性，避免了傳統RNN中的梯度消失或爆炸等問題。

????????所有循環神經網絡都具有神經網絡重復模塊鏈的形式。在標準 RNN 中，這個重復模塊將具有非常簡單的結構，例如單個 tanh 層。

????????LSTM 也具有這種鏈式結構，但重復模塊具有不同的結構。神經網絡層不是單一的，而是四個（黃色矩形，四個激活函數，三個sigmod、一個tanh），以非常特殊的方式相互作用。

????????LSTM每個循環的模塊內又有4層結構:3個sigmoid層，2個tanh層

????????基本狀態：下圖就是描述的關鍵部分：細胞狀態C?cell state
????????LSTM的關鍵是細胞狀態CC，一條水平線貫穿于圖形的上方，這條線上只有些少量的線性操作，信息在上面流傳很容易保持。

????????細胞狀態是LSTM的中心概念，它可以被視為一條信息的高速公路，沿著序列傳遞信息。細胞狀態的設計使得信息可以幾乎不受阻礙地在序列間流動，這解決了傳統RNN中梯度消失問題導致的信息傳遞障礙。

????????門：LSTM有通過精心設計的稱作“門”的結構來去除或者增加信息到細胞狀態的能力。
門是一種讓信息選擇式通過的方法。他們包含一個sigmoid神經網絡層和一個pointwise乘法操作。

????????Sigmoid層輸出0到1之間的數值，描述每個部分有多少量可以通過。
????????????????0 代表“不許任何量通過”；
????????????????1 代表“允許任何量通過”。
????????LSTM 擁有三個門，來保護和控制細胞狀態。

3.2?門控機制

3.2.1?遺忘門

????????遺忘門（Forget Gate）：決定細胞狀態中要保留的信息。它通過一個sigmoid函數來輸出一個0到1之間的值，表示要忘記（0）或保留（1）的程度。1 代表“完全保留這個”，而 0 代表“完全擺脫這個”。

????????這個函數是遺忘門（forget gate）的公式，用于確定哪些信息應當從單元的狀態中移除

[ ${h}_{t-1}, {x}_{t}$ ]：這是一個連接的向量，包括前一時間步的隱藏狀態 ${h}_{t-1}$ 和當前時間步的輸入 ${x}_{t}$ 。它們被合并起來，以便遺忘門可以考慮當前的輸入和先前的隱藏狀態來做出決策。
${W}_{f}$ ：這是遺忘門的權重矩陣，用于從輸入[ ${h}_{t-1}, {x}_{t}$ ]中學習什么信息應該被遺忘。
${b}_{f}$ ：這是遺忘門的偏置項，它被加到權重矩陣和輸入向量的乘積上，可以提供額外的調整能力，確保即使在沒有輸入的情況下遺忘門也能有一個默認的行為。
$\sigma$ ：這是sigmoid激活函數，它將輸入壓縮到0和1之間。在這里，它確保遺忘門的輸出也在這個范圍內，表示每個狀態單元被遺忘的比例。
${f}_{t}$ ：這是在時間步 ( t ) 的遺忘門的輸出，它是一個向量，其中的每個元素都在0和1之間，對應于細胞狀態中每個元素應該被保留的比例。

????????函數的整體目的是使用當前輸入和前一時間步的隱藏狀態來計算一個門控信號，該信號決定細胞狀態中的哪些信息應該被保留或丟棄。這是LSTM的關鍵特性之一，它允許網絡在處理序列數據時學習長期依賴關系。

3.2.2?輸入門

? ? ? ??輸入門（Input Gate）：決定要從輸入中更新細胞狀態的哪些部分。它結合了輸入數據和先前的細胞狀態，利用sigmoid函數來確定更新的量，并通過tanh函數來產生新的候選值，然后結合遺忘門確定最終的更新。

????????

輸入門的激活 $({i} _{t} )$ ： $i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)$
候選細胞狀態 $( {C}_{t} )$ ： $\tilde{C}_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C)$

????????解釋如下：

${i} _{t}$ 表示時間步 ( t ) 的輸入門激活值，是一個向量。這個向量通過sigmoid函數產生，將值限定在 0 和 1 之間。它決定了多少新信息會被加入到細胞狀態中。
${W}_{i}$ 是輸入門的權重矩陣，用于當前時間步的輸入 ${x}_{t}$ 和前一個時間步的隱藏狀態 ${h}_{t-1}$ 。
[ ${h}_{t-1}, {x}_{t}$ ] 是前一個隱藏狀態和當前輸入的串聯。
${b}_{i}$ 是輸入門的偏置向量。
$\widetilde{} {?{C}_{t}}$ 是候選細胞狀態，它是通過tanh函數產生的，可以將值限定在 -1 和 1 之間。它與輸入門 ${i}_{t}$ 相乘，決定了將多少新的信息添加到細胞狀態中。
${W}_{C}$ 是控制候選細胞狀態的權重矩陣。
${b}_{C}$ 是對應的偏置向量。

3.2.3?狀態更新

????????在每個時間步，LSTM單元都會計算這兩個值，并結合遺忘門 $f_t$ 的值更新細胞狀態 $C_t$ 。這樣，LSTM能夠記住長期的信息，并在需要的時候忘記無關的信息。

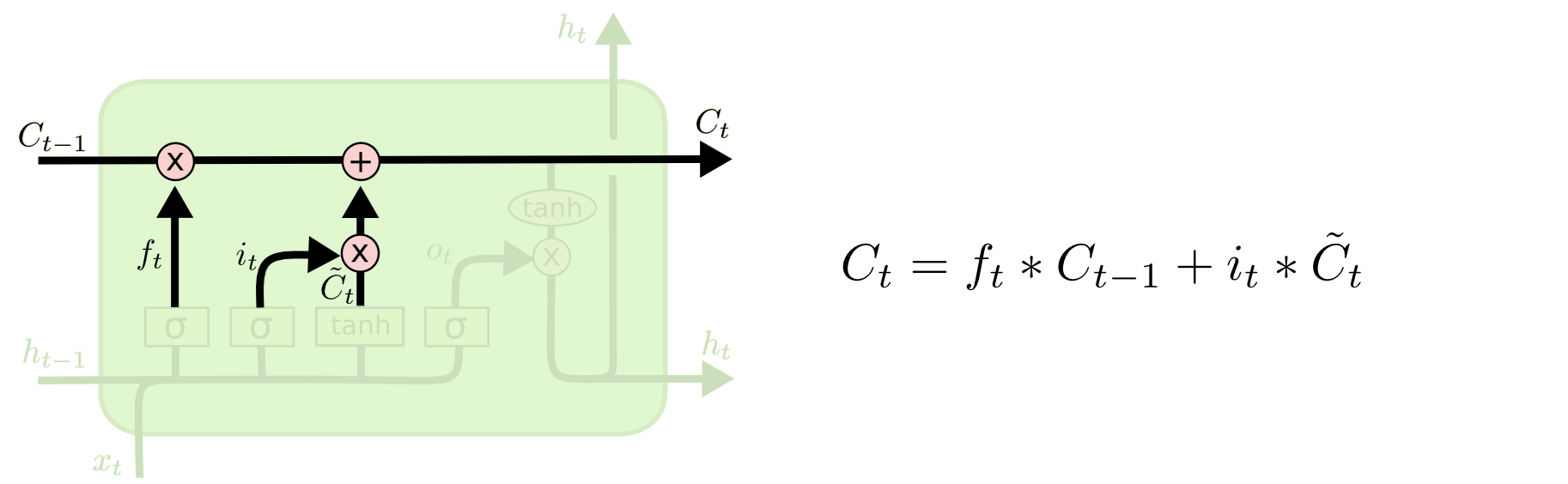
????????在計算新的細胞狀態 ( ${C}_{t}$ ) 時使用的更新規則： $C_t = f_t * C_{t-1} + i_t * \tilde{C}_t$

????????這里：

${C}_{t}$ 是當前時間步的細胞狀態。
${C}_{t-1}$ 是上一個時間步的細胞狀態。
${f}_{t}$ 是遺忘門的激活值，通過sigmoid函數計算得到。它決定了多少之前的細胞狀態應該被保留。
${i}_{t}$ 是輸入門的激活值，也是通過sigmoid函數得到的。它決定了多少新的信息應該被存儲在細胞狀態中。
${C}_{t}$ 是當前時間步的候選細胞狀態，通過tanh函數得到。它包含了潛在的新信息，可以被添加到細胞狀態中。

????????符號 * 代表元素間的乘積，意味著 ${f}_{t}$ 和 ${i}_{t}$ 分別與 ${C}_{t-1}$ 和 ${C}_{t}$ 相乘的結果然后相加，得到新的細胞狀態 ${C}_{t}$ 。這個更新規則使得LSTM能夠在不同時間步考慮遺忘舊信息和添加新信息，是它在處理序列數據時記憶長期依賴信息的關鍵。

3.2.4?輸出門

????????輸出門（Output Gate）：決定在特定時間步的輸出是什么。它利用當前輸入和先前的細胞狀態來計算一個輸出值，然后通過sigmoid函數來篩選。

????????這個函數描述了LSTM（長短期記憶）網絡的輸出門和隱藏狀態的計算。

輸出門 ${o}_{t}$ 的計算： $o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o)$ ；
隱藏狀態 {h}_{t} 的計算： $h_t = o_t * \tanh(C_t)$

????????具體來說：

${o}_{t}$ 是輸出門的激活值。這是通過將前一時間步的隱藏狀態 ${h}_{t-1}$ 和當前時間步的輸入 ${x}_{t}$ 連接起來，并應用權重矩陣 $W_o$ 以及偏置項 $b_o$ ，然后通過sigmoid函數 $\sigma$ 來計算的。Sigmoid函數確保輸出值在0和1之間。
${C}_{t}$ 是當前時間步的細胞狀態，這是在之前的步驟中計算的。
${C}_{t}$ 是細胞狀態的tanh激活，這個激活函數將值壓縮到-1和1之間。這是因為細胞狀態 $C_t$ 可以有很大的值，而tanh函數有助于規范化這些值，使它們更加穩定。
${h}_{t}$ 是當前時間步的隱藏狀態，通過將輸出門 ${o}_{t}$ 的值與細胞狀態的tanh激活相乘來得到。這個元素級別的乘法（Hadamard乘法）決定了多少細胞狀態的信息將被傳遞到外部作為當前的隱藏狀態輸出。

????????這種結構允許LSTM單元控制信息的流動，它可以通過輸出門來控制有多少記憶單元的信息會被傳遞到隱藏狀態和網絡的下一個時間步。

3.2.5?LSTM總結

3.3?代碼實現

????????注意：矩陣乘法規則：矩陣 A 和向量 v 做點積運算時，A 的列數必須與 v 的長度一致。

3.3.1?原生代碼

????????多對一的任務：

import numpy as npclass LSTM:def __init__(self, input_size, hidden_size, out_size):""":param input_size: 詞嵌入之后的向量維度:param hidden_size: 隱藏層的維度:param out_size: 輸出的分類數"""self.input_size = input_sizeself.hidden_size = hidden_sizeself.out_size = out_size# 權重矩陣和偏置# 遺忘門self.W_f = np.random.randn(self.input_size + self.hidden_size, self.hidden_size)self.b_f = np.zeros((self.hidden_size,))# 輸入門self.W_i = np.random.randn(self.input_size + self.hidden_size, self.hidden_size)self.b_i = np.zeros((self.hidden_size,))# 候選狀態self.W_c = np.random.randn(self.input_size + self.hidden_size, self.hidden_size)self.b_c = np.zeros((self.hidden_size,))# 輸出門self.W_o = np.random.randn(self.input_size + self.hidden_size, self.hidden_size)self.b_o = np.zeros((self.hidden_size,))# 輸出層self.W_out = np.random.randn(self.hidden_size, self.out_size)self.b_out = np.zeros((self.out_size,))def tanh(self, x):return np.tanh(x)def sigmoid(self, x):return 1 / (1 + np.exp(-x))def forward(self, x):# 初始細胞狀態和隱藏狀態h_t = np.zeros((self.hidden_size,))c_t = np.zeros((self.hidden_size,))h_all = []  # 存儲每個時間步的隱藏狀態c_all = []  # 存儲每個時間步的細胞狀態for t in range(x.shape[0]):x_t = x[t]  # 獲取時間步# 拼接輸入和隱藏狀態x_t = np.concatenate((x_t, h_t), axis=0)# 遺忘門f_t = self.sigmoid(np.dot(x_t, self.W_f) + self.b_f)# 輸入門i_t = self.sigmoid(np.dot(x_t, self.W_i) + self.b_i)# 候選狀態c_ti = self.tanh(np.dot(x_t, self.W_c) + self.b_c)# 更新細胞狀態c_t = f_t * c_t + i_t * c_ti# 輸出門o_t = self.sigmoid(np.dot(x_t, self.W_o) + self.b_o)# 更新隱藏狀態h_t = o_t * self.tanh(c_t)# 保留每個時間步的結果h_all.append(h_t)c_all.append(c_t)# 輸出層 多對一的任務 最后一個時間步的隱藏層狀態作為輸入 進行分類y_t = np.dot(h_t, self.W_out) + self.b_outreturn y_t, h_all, c_all# 測試
if __name__ == '__main__':# 數據輸入x = np.random.rand(3, 2)  # 三個單詞 每個單詞兩個維度 注意：在forward方法for循環中x.shapr[0]的表示是什么lstm = LSTM(input_size=2, hidden_size=5, out_size=10)y_t, h_all, c_all = lstm.forward(x)print(y_t)print(h_all)print(c_all)

????????多對多：

import torch
from torch import nnclass LSTMModule(nn.Module):def __init__(self, hidden_size, input_size, out_size):super(LSTMModule, self).__init__()self.hidden_size = hidden_sizeself.out_size = out_sizeself.input_size = input_sizeself.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_size, batch_first=True)self.fc = nn.Linear(hidden_size, out_size)def forward(self, x):out, (h_last, c_last) = self.lstm(x)# 多對多的輸出out = self.fc(out)# 多對一的輸出# out = torch.mean(out, dim=1)# out = self.fc(out)return out# 測試
if __name__ == '__main__':x = torch.randn(10, 6, 2)lstm = LSTMModule(input_size=2, hidden_size=5, out_size=8)y_t = lstm.forward(x)print(y_t.shape)

????????一對多：在一對多的任務中，盡管輸入序列的大小只有一個，但模型仍然可以生成多個輸出。這通常涉及以下幾個方面：

1. 輸入與時間步

一對多任務通常指的是在某個時間點有一個輸入，但模型在接下來的多個時間步中生成多個輸出。例如，在圖像生成或文本生成任務中，你可能在每次預測時只輸入一個數據點（如一個單詞或圖像），然后模型根據這個輸入生成多個輸出。

2. 時間步的生成

對于輸入序列只有一個時間步的情況，模型可以通過在其內部實現循環來生成多個時間步的輸出。通常在 LSTM 中，這通過反饋機制實現：
- 在每次生成輸出時，模型可以使用先前生成的輸出作為下一步的輸入。

3. 示例：文本生成

????????例如，在文本生成中，你可能會輸入一個起始單詞（例如 "Once"），然后 LSTM 根據這個單詞生成接下來的多個單詞：

輸入：["Once"]
輸出：["Once", "upon", "a", "time", "there", "was"]

????????在這種情況下，盡管輸入只有一個時間步，但后續的多個輸出是根據模型的狀態和歷史信息生成的。

4. 實現方式

????????在實現時，可以設置一個循環，在每個時間步中，模型接收前一個時間步的輸出作為當前時間步的輸入。這樣，即使起始時只有一個輸入，模型也可以生成多個輸出。

output_sequence = []  
hidden_state, cell_state, output = lstm.forward(input_char)output_sequence.append(np.argmax(output,axis=1))  # 選擇概率最大的字符

3.3.2?基于 pytorch API 代碼實現

????????在 LSTM 網絡中，初始化隱藏狀態 (h0) 和細胞狀態 (c0) 是一個重要的步驟，確保模型在處理序列數據時有一個合理的起始狀態。

h0 = torch.zeros(1, x.size(1), self.hidden_size)
c0 = torch.zeros(1, x.size(1), self.hidden_size)

1：指的是 LSTM 的層數。如果 num_layers > 1，那么這里應該是 num_layers。

x.size(1)：表示批次的大小 (batch_size)。這是輸入 x 的第二個維度，因為 x 的形狀為 (seq_len, batch_size, input_size)。

self.hidden_size：表示 LSTM 隱藏層的單元數，即隱藏狀態和細胞狀態的維度。

在 PyTorch 中，使用 LSTM (長短期記憶網絡) 進行序列數據的處理時，調用 self.lstm(x, (h0, c0)) 會返回兩個值：out 和 (hn, cn)。

out:

out 是 LSTM 網絡在所有時間步的輸出。
假設輸入 x 的形狀是 (seq_len, batch_size, input_size)，那么 out 的形狀將是 (seq_len, batch_size, num_directions * hidden_size)，其中 num_directions 是 1 如果 LSTM 是單向的，2 如果是雙向的。
具體地，out 包含 LSTM 在每個時間步的輸出，適用于后續處理（例如，將其傳遞給一個全連接層）。

(_)或(hn, cn):

hn 是最后一個時間步的隱狀態(hidden state)。
cn 是最后一個時間步的細胞狀態(cell state)。
如果輸入 x 的形狀是 (seq_len, batch_size, input_size)，那么 hn 和 cn 的形狀將是 (num_layers * num_directions, batch_size, hidden_size)

單層 LSTM：如果 num_layers = 1，LSTM 網絡將只有一個層。這意味著輸入序列直接通過這個單層 LSTM 進行處理。

多層 LSTM：如果 num_layers > 1，LSTM 網絡將有多層。輸入序列首先通過第一層 LSTM，第一層的輸出作為輸入傳遞給第二層，以此類推，直到最后一層。
這些狀態可以用于初始化下一個序列的 LSTM，特別是在處理長序列或多個批次的序列數據時。

3.4?序列池化

????????在自然語言處理 (NLP) 中，序列池化（sequence pooling）是一種將變長序列轉換為固定長度表示的方法。這個過程對于處理可變長度的輸入（如句子或文檔）特別有用，因為許多深度學習模型（如全連接層）需要固定長度的輸入。

????????序列池化的主要方法包括：

最大池化（Max Pooling）：
- 對序列中的每個特征維度，選擇該維度的最大值作為輸出。
- 適用于突出序列中特定特征的最大激活值。
- 例如，如果輸入是長度為 5 的序列，且每個時間步的特征維度為 10，最大池化會對每個特征維度取最大值，輸出形狀為 (batch_size, feature_size)。
平均池化（Average Pooling）：

對序列中的每個特征維度，計算該維度的平均值作為輸出。
適用于希望保留序列中所有特征的總體信息。
同樣，對于長度為 5 的序列，特征維度為 10，平均池化會對每個特征維度取平均值，輸出形狀為 (batch_size, feature_size)。
```
import torch
from torch import nn# [b,s,d]
x = torch.randn(10, 6, 5)
# 調用平均池化方法
# pool = nnAvgPool1d(2, stride=2)
pool = nn.AdaptiveAvgPool1d(1)# 調整形狀去匹配池化輸入 --->[b,d,s]
x = x.permute(0, 2, 1)
out = pool(x)
out = out.squeeze(2)
print(out)
print(out.shape)
```
3.注意力池化（Attention Pooling）：
- 使用注意力機制對序列進行加權平均，根據每個時間步的重要性分配權重。
- 適用于希望模型能夠根據輸入內容自適應地分配注意力權重。
- 注意力池化的實現通常涉及一個注意力權重計算模塊和一個對這些權重進行加權平均的模塊。

3.5?梯度消失

????????LSTM（長短期記憶網絡）是一種特殊的RNN（循環神經網絡），設計初衷就是為了解決傳統RNN在長序列數據上訓練時出現的梯度消失和梯度爆炸問題。然而，盡管LSTM相較于普通的RNN在處理長序列數據時表現得更好，但它仍然有可能在某些情況下出現梯度消失和梯度爆炸的問題。原因可以歸結為以下幾個方面：

3.5.1?梯度消失問題

????????梯度消失（Vanishing Gradient）主要在于反向傳播過程中，梯度在多層傳播時會逐漸減小，導致前面層的參數更新非常緩慢，甚至完全停滯。LSTM盡管通過門控機制（輸入門、遺忘門和輸出門）緩解了這個問題，但仍然可能出現梯度消失，特別是在以下情況下：

????????- 長期依賴問題：如果序列特別長，即使是LSTM也可能無法有效地記住早期的信息，因為梯度會在很長的時間步長內持續衰減。
????????- 不適當的權重初始化：如果權重初始化不合理，可能會導致LSTM的各個門在初始階段就偏向于某種狀態（如過度遺忘或完全記住），從而影響梯度的有效傳播。
????????- 激活函數的選擇：盡管LSTM通常使用tanh和sigmoid激活函數，這些函數在某些輸入值下可能會導致梯度的進一步縮小。