信息量

對于一個事件而言，它一般具有三個特征：

• 小概率事件往往具有較大的信息量

• 大概率事件往往具有較小的信息量

• 獨立事件的信息量相互可以相加

比如我們在買彩票這個事件中，彩票未中獎的概率往往很高，對我們而言一點也不稀奇，給我們帶來的信息量很小，彩票中大獎的概率往往非常低，中一次大獎則是非常罕見，給我們帶來的信息量很大。

如何描述信息量大小呢？有如下定義：

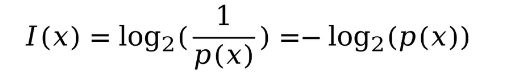
其中描述某一事件發生的概率，反映了信息量與發生概率之間成反比，取對數是為了?獨立事件的信息量相互可以相加（第三個特征）。

有如下例子：

拋一枚硬幣，根據正面朝上和反面朝上的概率計算其信息量

其中，當正反概率相等時，信息量對等；當正反概率不等時，概率越小的事件其信息量越大。

當我們對信息量這一概念有一個初步理解后，我們繼續往下看關于熵的定義

?香農熵（Shannon Entropy）

熵：針對一個概率分布所包含的平均信息量

相當于計算一個概率分布中信息量的期望

由于熵這一概念是由科學家香農所提出，故熵又被稱作香農熵（注意這里的熵與物理學中的熵不是同一個意思）。

?對于離散的概率分布，計算香農熵的公式如下所示：

?對于連續的概率分布，計算香農熵的公式如下所示：?

以離散的概率分布為例，我們可以看到，計算香農熵就是將每個事件的概率乘以其對應的信息量并進行向加求得。

我們同樣回到拋硬幣的例子：

計算每種情況的香農熵

?通過以上例子我們不難發現：

在一個概率分布中，當概率密度函數分布比較均勻的時候，隨機事件發生的情況變得更加不確定，相應地，對應的熵更大；當概率密度函數分布比較聚攏的時候，隨機事件發生的情況變得更加確定，相應地，對應的熵更小。

現在我們對熵的概念也有了一個基本的了解，我們繼續往下看交叉熵。

交叉熵（Cross Entropy）

我們先不急著看概念，我們先看一個例子，同樣是拋硬幣的例子：

如果我們事先并不知道每個事件真實的概率p，我們可以先對其進行估計q，并計算在q下的信息量I，那我們可以計算在真實概率分布p下的平均信息量的估計，這個估計就稱作交叉熵。

我們看一下交叉熵的公式（離散概率分布）：

連續概率分布交叉熵計算公式如下：

我們利用估計的信息量計算在真實概率下的熵便稱為交叉熵。

根據上面的公式，我們計算一下在不同估計下的交叉熵：

從中我們可以發現，在不同估計下計算的交叉熵要大于香農熵（可以看下在之前在計算不同概率分布下的香農熵）。這是為什么呢？我們接著往下看。

KL散度（Kullback-Leibler Diergence）

一種定量衡量兩個概率分布之間差異的方法：交叉熵與熵之間的差異。

如果理解了之前的熵和交叉熵，KL散度的定義也相對容易理解。

離散概率分布下的KL散度的計算公式如下：

連續概率分布下的KL散度的計算公式如下：

直觀理解KL散度，可以看作在Q表示P所損失的信息量，KL 散度越大，說明 P和 Q的差異越大

KL散度有如下性質：

KL散度永遠大于等于0 ，可通過吉布斯不等式證明。

這也就說明了為什么在不同估計下計算的交叉熵要大于等于香農熵，只有當p和q相等時，交叉熵才等于香農熵。

p和q交換后得出的KL散度不相等，因此KL散度不能看作距離，但可以用來優化模型

在機器學習中，如果想要優化一個模型，KL散度是一個重要的衡量標準，可通過最小化KL散度使模型最優。其中，在優化過程中，我們對其q進行梯度優化，由于p與q無關，故為0，最終梯度優化公式如下：