目錄
1.算法仿真效果
2.算法涉及理論知識概要
2.1?混沌映射
2.2 基于混沌映射的LDPC編譯碼
3.MATLAB核心程序
4.完整算法代碼文件獲得
1.算法仿真效果
matlab2022a仿真結果如下(完整代碼運行后無水印):
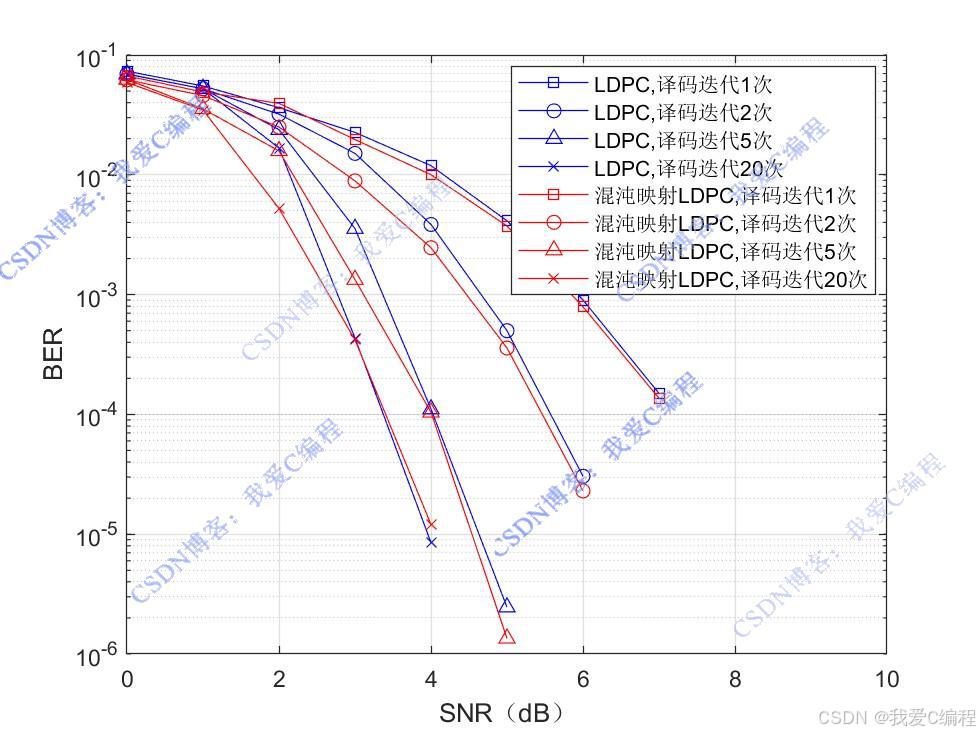
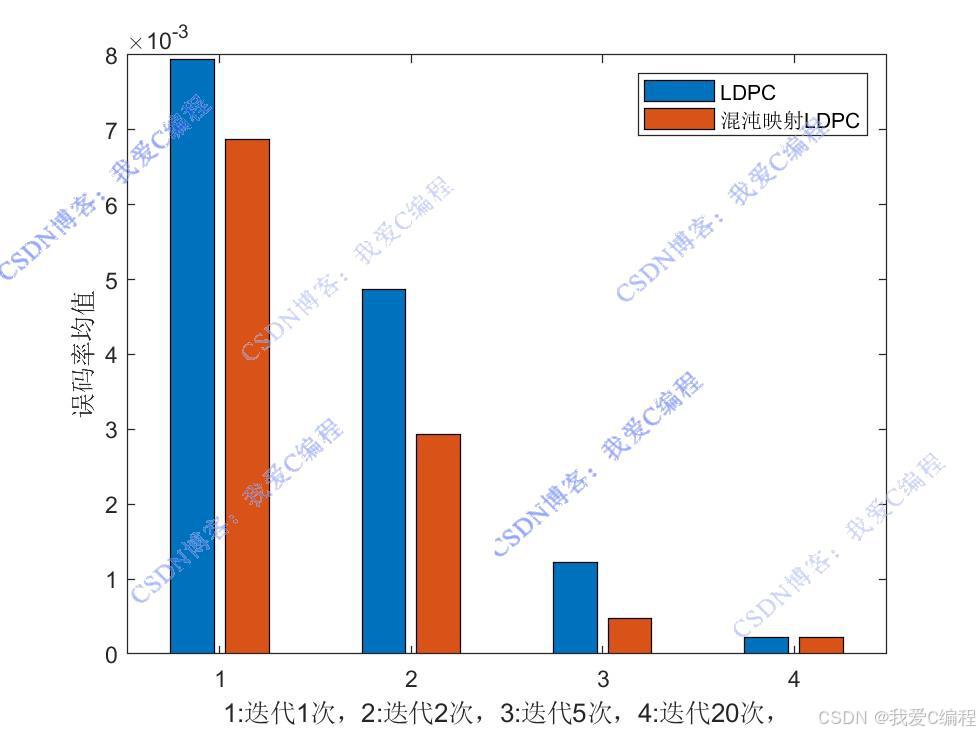
仿真操作步驟可參考程序配套的操作視頻。
2.算法涉及理論知識概要
? ? ? ?在現代通信系統中,信道編碼是提高通信可靠性的關鍵技術之一。低密度奇偶校驗(LDPC)碼作為一種性能接近香農極限的線性分組碼,在各種通信系統中得到了廣泛應用。然而,傳統的 LDPC 碼在某些復雜信道環境下性能仍有待提高。混沌映射由于其具有對初始條件敏感、遍歷性和隨機性等特點。為了進一步提升LDPC碼的抗干擾能力,引入混沌映射是一種有效的方法。混沌系統具有對初始條件敏感、遍歷性和偽隨機性等特性,將其生成的二進制序列與原始數據進行異或操作,再進行LDPC編碼,能夠增強數據的隨機性和抗干擾能力,提高通信系統的可靠性。
2.1?混沌映射
? ? ? 混沌映射是一種確定性的非線性動力學系統,它能夠產生看似隨機的序列。常見的混沌映射有 Logistic映射、Tent映射等。Logistic映射的定義為:

混沌序列具有以下特性:
對初始條件敏感:初始條件的微小變化會導致混沌序列的巨大差異。
遍歷性:混沌序列能夠在其取值范圍內均勻遍歷。
隨機性:混沌序列具有類似隨機序列的統計特性。
2.2 基于混沌映射的LDPC編譯碼
具體步驟如下:
1.選擇合適的混沌映射,如Logistic映射,并確定初始條件x0?和控制參數μ;
2.生成長度為N的混沌序列?{xn?}n=0N?1;
3.對混沌序列進行量化處理,將其映射到有限集合?{0,1}?上,得到二進制序列?{bn?}n=0N?1;其過程如下:

4.根據二進制序列對待編碼的數據進行異或;其過程如下:

5.將異或后的數據進行LDPC編碼;
6.進行LDPC譯碼;
7.將譯碼后的數據和混沌序列產生的二進制數據進行異或,恢復出初始的發射數據。
? ? ? ?基于混沌映射的LDPC信道編譯碼方法,通過將原始數據與混沌二進制序列進行異或操作,再進行LDPC編碼,有效地提高了通信系統的抗干擾能力和安全性。該方法結合了混沌系統的特性和 LDPC碼的優勢,在復雜的信道環境下具有良好的性能。
3.MATLAB核心程序
.......................................................................while Num_err <= TJL(i) fprintf('SNR = %f\n', SNR(i));Num_errTrans_data = round(rand(N-M,1)); %產生需要發送的隨機數% 混沌映射生成序列chaos_seq = logistic_map(mu, x0, N-M);% 將混沌序列二值化chaos_bits = (chaos_seq > 0.5);[ldpc_code,newH] = func_Enc(scrambled_bits',H); %LDPC編碼u = [ldpc_code;scrambled_bits']; %LDPC編碼Trans_BPSK = 2*u-1; %BPSK%LDPC譯碼 [vhat,nb_iter] = func_Dec(Rec_BPSK,newH,N0,Max_iter,mu);descrambled_bits = bitxor(vhat(M+1:N), chaos_bits);endBit_err(i) = Num_err/(N*Numbers);
endfigure;
semilogy(SNR,Bit_err,'o-');
xlabel('SNR(dB)');
ylabel('BER');
grid on;
hold on;
if Max_iter==1save data1.mat SNR Bit_err
end
if Max_iter==2save data2.mat SNR Bit_err
end
if Max_iter==5save data5.mat SNR Bit_err
end
if Max_iter==20save data20.mat SNR Bit_err
end
0X_085m4.完整算法代碼文件獲得
V



)

)













機器人仿真器存在的問題)