學點概率論，打破認識誤區

概率論是統計分析和機器學習的核心。掌握概率論對于理解和開發穩健的模型至關重要，因為數據科學家需要掌握概率論。本博客將帶您了解概率論中的關鍵概念，從集合論的基礎知識到高級貝葉斯推理，并提供詳細的解釋和實際示例。

·簡介
·基本集合論
·基本概率概念
·隨機變量和期望
·邊際、聯合和條件概率
·概率規則：邊際化和乘積
·貝葉斯定理
·概率分布
·使用概率進行學習
?? ·貝葉斯推理
·在 Python 中實現概率概念
·玩具示例：拋硬幣的貝葉斯推理
·結論
·行動呼吁

介紹

概率論是量化不確定性的數學框架。它使我們能夠對隨機現象進行建模和分析，在統計學、機器學習和數據科學中不可或缺。概率論幫助我們做出明智的決策、評估風險并建立預測模型。

基本集合論

首先，讓我們定義幾個關鍵術語。

集合(Set)是對象的集合。這些對象稱為集合的元素。

集合a的子集b是其元素均為a的元素的集合，即𝑏 ? 𝑎。

空間?S?是最大的集合；因此，所有其他集合都在考慮之中𝑠? ? 𝑆。

空集?O?是空集或零集。O不?包含任何元素。

讓我們將集合論的組成部分形象化。

維恩圖描繪了集合邏輯和運算。最上面的圖顯示樣本空間S，其中集合A、B和C作為子集（即，B是A的子集，而C是B的子集；因此， C 是A的子集）。其余行描繪了兩個集合，A和B。文本包含每個集合的描述和數學。作者創建了視覺效果。

上圖描繪了我們在使用集合時遇到的各種場景。讓我們來描述集合論的不同方面。鼓勵讀者在閱讀定義和回顧數學表達式時參考每個小節后面的視覺圖，以加深他們的直覺。

子集

子集𝑏 ? 𝑎，或者集合a?包含b，如果b的所有元素也是a的元素，則𝑎 ? 𝑏。也就是說，

英文：語句“如果b???a，且c???b，則c???a?”表達了集合包含的傳遞性。如果集合b是集合a的子集，集合c是集合b的子集，則c也一定是a的子集。第二項“以下關系成立：a???a，0???a，a???S?”強調了集合包含的基本性質。因此：

a???a表示每個集合都是其自身的子集。
0?a表示空集是任意集合a的子集。
a?S表示任意集合a都是全集S的子集。

集合運算

相等：兩個集合相等，則a?的每個元素都必須在b中，而b的每個元素都必須在a中。從數學上來說：

并集（和）：兩個集合a?和b的并集是由a或b?或兩者的所有元素組成的集合。并集運算滿足以下性質：

集合a?和b的交集（積）由集合a和b共有的所有元素組成。交集運算滿足以下屬性：

互斥集

如果兩個集合a和b沒有共同元素，我們稱它們互斥或不相交，即

補充

集合 a 的補集 a 定義為由 S 中所有不屬于 a 的元素組成的集合。補集滿足以下性質：

兩集合之差

a???b的差集是a中不屬于b的元素的集合。差集滿足以下性質：

基本概率概念

樣本空間（S）：隨機實驗的所有可能結果的集合。

事件（E）：樣本空間的子集，包含特定結果或一組結果。

隨機變量 (RV)：可能值為隨機現象的數值結果的變量。例如：人的身高、拋硬幣或擲骰子的結果。

事件的概率

事件E的概率（即P(E)）是衡量該事件發生可能性的指標。它滿足以下性質：

例子

考慮一個公平的六面骰子。樣本空間為S = {1, 2, 3, 4, 5, 6}。擲出 3 的概率為 P({3}) = 1/6。擲出 1 或 3 呢？P({1, 3}) = 2/6 = 1/3。最后，擲出偶數呢？P({2, 4, 6}) = 3/6 = 1/2。

隨機變量和期望

請注意，我們在本部分中使用了求和與積分。請參閱本系列的上一部分，其中涵蓋了微積分和線性代數。

機器學習的基礎數學

深入探究向量范數、線性代數、微積分

pub.towardsai.net

隨機變量（RV）

RV 是一種變量，其值由隨機實驗的結果決定。有兩種類型：離散隨機變量（取可數個值）和連續隨機變量（取不可數個值）。

例如離散隨機變量的分布：

它可以取每個值的概率。
符號：P(X=xi)。
這些數字滿足以下條件：

期望和方差

期望值（平均值）：隨機變量的平均值。

對于離散隨機變量：

這個期望值（即平均值）是一個離散隨機變量X 。因此，我們將其計算為所有可能值x乘以其各自概率P(X = x)的加權總和。

對于連續隨機變量：

這個期望值（即平均值）是連續隨機變量X的。我們將其計算為x乘以其概率密度函數f(x)在整個可能值范圍內的積分。

總之：

方差：我們可以計算一個二階統計測量，表示隨機變量與預期值的偏離。

上述方程表示隨機變量X的方差，測量X值圍繞其均值E[X]的擴展或分散。

例子

對于一個公平的六面骰子，預期值是：

邊際概率、聯合概率和條件概率

在本小節中，我們將使用一張圖來解釋邊際概率、聯合概率和條件概率。因此，表格是兩個 RV 的聯合概率分布，正如作者在此處所描繪的那樣。

檢查上面的圖片。我們將使用這個視覺效果來學習概率論的基本概念：邊際概率、聯合概率和條件概率。這些概念對于理解隨機變量之間的關系至關重要，尤其是在處理分類或計數數據時。

邊際概率

邊際概率是指在不考慮任何其他事件的情況下，單個事件發生的概率。在圖中，p(X = x?)表示它。然后，我們計算如下：

這表示隨機變量X取特定值x?的概率，該概率被邊緣化為其他變量的所有可能值。因此，它有助于通過將該事件的聯合概率與另一個變量的所有可能結果相加來找到單個事件的概率。

聯合概率

聯合概率是兩個事件同時發生的概率。參考上圖，它是概率p(X = x?, Y = y?)，計算如下：

這個聯合概率衡量兩個事件X = x?和Y = y?同時發生的可能性。

條件概率

條件概率衡量在另一個事件已經發生的情況下，發生另一事件的概率。圖像將其定義為p(Y = y? | X = x?)，計算方法如下：

該公式顯示在X = x?已經發生的情況下，Y = y?的可能性有多大。

概率規則：邊緣化和產品

邊緣化是概率論中用到的一個過程，用于從所有變量的聯合概率分布中推導出與變量子集相關的事件的概率。

在這個等式中，我們通過對另一個變量Y的所有可能值求和來計算邊際概率p(X = x?)：

乘積規則是概率中的一個基本概念，它使我們能夠根據邊際概率和條件概率來表示兩個事件的聯合概率。

該等式顯示了聯合概率p(X = x?, Y = y?)如何分解：

具體來說，用數學的方式表達，乘積法則允許使用一個事件的邊際概率和在第一個事件的條件下另一個事件的條件概率來計算兩個事件的聯合概率。

概括

這些概念是概率論的基礎，對于理解數據科學中更復雜的概率模型和推理技術至關重要。總結如下。

最后，如果P(Y | X) = P(Y)?，則𝑋和𝑌是獨立的，這意味著P(Y | X) = P(Y)。這意味著P(𝑋, 𝑌) = P(X)P(Y)。

貝葉斯定理

貝葉斯定理是貝葉斯推理的基石，是一個強大的概率結構，它使我們能夠將先驗知識融入到我們的計算中。

回到條件概率并在此基礎上構建：回想一下我們之前定義的p(Y = y? | X = x?)。我們可以使用事件A和B來概括這一點，并將其進一步擴展到貝葉斯。

因此，條件概率量化了在另一事件發生的情況下發生某事件的概率。因此，在事件B發生的情況下，事件 A的概率是A和B的聯合概率與B的概率之比。我們將其表示為P(A | B)，并定義為：

管道字符“|”在概率論中翻譯為“給定”。

因此，貝葉斯定理將兩個事件的條件概率關聯如下：

該術語根據似然P?(B |?A)、先驗P(A)和邊際概率P(B)來表達條件概率P(A | B)?。同樣，這個構造是貝葉斯推理的基礎，它使我們能夠根據新證據更新我們的信念。

例子

假設我們對某種疾病進行測試，其概率如下：

利用貝葉斯定理，我們可以找到P(疾病|陽性)：

我們可以這樣計算P(Positive)?：

該方程表示考慮兩種情況（即患有和不患有疾病）的檢測呈陽性的總概率：直接應用總概率定律。

概率分布

典型趨勢遵循已知分布。因此，一個常見的問題是假設一個特定的分布來擬合我們的數據。以下是離散和連續隨機變量的幾個分布。

離散分布

二項分布：描述固定次數的獨立伯努利試驗中的成功次數。
泊松分布：對固定時間間隔或空間內發生的事件數量進行建模。

連續分布

正態分布：以鐘形曲線為特征，用平均值 μ 和標準差 σ 描述。
指數分布：描述泊松過程中事件之間的時間。

我們可以通過了解期望值、方差或其他統計指標來近似數據分布。以下備忘單總結了一些連續和離散 RV 的備忘單。

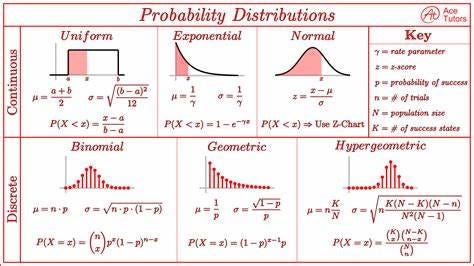
這是顯示連續和離散概率分布的圖表。每個分布都有其平均值、標準差和概率的公式——圖片來源。

例子

讓我們仔細看看正態分布的概率密度函數。從數學上講，它表示如下：

使用正態分布的概率概念可視化，顯示概率密度函數 (PDF)、累積分布函數 (CDF)、平均值 (μ) 和標準差 (σ)。

該圖以正態分布為基礎，直觀地展現了關鍵的概率概念。圖中藍色部分為概率密度函數 (PDF)，表示分布中不同結果出現的可能性。PDF 曲線下方的面積表示隨機變量落在特定范圍內的概率。

累積分布函數 (CDF) 以紅色顯示。它從左到右累積概率，從 0 開始，漸近于 1。CDF 幫助我們確定隨機變量小于或等于某個值的概率。

垂直虛線標記平均值 (μ) 和與平均值的標準差 (σ)。平均值在 x=0 處用紅色虛線表示，而綠色、橙色和紫色虛線分別表示第一、第二和第三個標準差 (±1σ、±2σ、±3σ)。這些標準差說明了數據如何分布在平均值周圍，其中約 68%、95% 和 99.7% 分別在平均值的 1σ、2σ 和 3σ 范圍內。

圖中的箭頭有助于識別這些關鍵點，使視覺效果更易于理解。對于任何想要掌握概率基本概念的人來說，該圖都是一個有用的工具，尤其是正態分布，它是統計分析和許多機器學習算法的基石。

使用概率進行學習

例如，在對垃圾郵件進行分類時，我們可以估計𝑃(𝑌 | 𝑉𝑖𝑎𝑔𝑎𝑟𝑎, 𝑙𝑜𝑡𝑡𝑒𝑟𝑦)。

— 如果𝑃(𝑌 | 𝑋) <0.5?，我們會將示例歸類為垃圾郵件。 — 但是，對𝑃(𝑋 | 𝑌)
進行建模通常更容易。

這就給我們帶來了最大似然法。

最大似然法

例如：拋硬幣

根據n 次拋硬幣的結果（其中h次都是正面），估計硬幣擲出“正面”的概率p 。

數據的可能性：

對數似然：

取導數并將其設置為 0：

貝葉斯推理

貝葉斯推理是一種統計推斷方法，其中貝葉斯定理用于隨著更多證據的出現而更新假設的概率。

先驗、似然和后驗

先驗（P（H））：對假設的初始信念。
可能性（P（E?|?H））：根據假設觀察到證據的概率。
后驗（P（H?|?E））：觀察證據后對假設的更新信念。

貝葉斯推理中的貝葉斯定理：

我們是如何得到這個結果的？讓我們回到使用X和Y進行泛化。

根據乘積法則

和

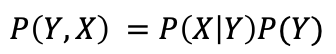
所以：

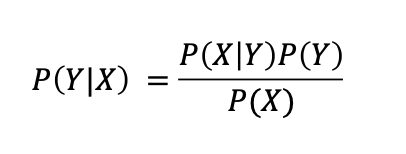
這被稱為貝葉斯規則。

總之：

𝑷(𝑿) 可以計算為

然而，推斷標簽并不重要。

例子

讓我們回到我們的案例，我們正在接受罕見疾病的檢測。這一次，我們的檢測結果已經呈陽性。讓我們使用貝葉斯來確定它是真陽性的概率（即使用貝葉斯檢查測試是否為假陽性，即測試結果被錯誤地歸類為真）。

在假陽性率為 5% 的測試中檢測結果為陽性。
出現這種疾病的可能性有多大？
假設每 100 人中就有 1 人患有此病。這會有什么不同嗎？
該測試的假陰性率為 10%；實際上，十分之一的錯誤預測是正確的。這可以用來改善我們的預測嗎？

我們首先從視覺上看一下。

該圖片顯示，每 100 人中就有 5 人被錯誤地標記為患有該疾病（即假陽性），而 1 人確實患有該疾病。

讓我們使用貝葉斯定理。

請查看《我們擁有什么和想要什么》。

讓我們進一步研究一下。

因此，先驗（即分母中的P(B)）由兩個子集組成，我們可以將其表示為并集（或和）。

現在，插上電源并喝水：

因此，我們患病的概率為 15.4%！這比僅考慮假陽性率而不使用檢測陽性和假陰性的百分比時原來的 95% 要好得多。

如果我們接受兩次檢測，每次都得到陽性結果，那會怎樣？這種疾病存在的可能性有多大？

其中A患有該疾病，而B兩次檢測結果呈陽性。

請注意，即使經過兩次測試，我們的機會仍然低于原來的 95%。

這就是貝葉斯的美妙之處：隨著我們獲得更多知識，我們可以將其融入到我們的數字理解中，從而提高概率的精確度！

在 Python 中實現概率概念

我們將使用該numpy庫進行數值計算和scipy.stats概率分布。

示例：拋硬幣模擬

<span style="color:rgba(0, 0, 0, 0.8)"><span style="background-color:#ffffff"><span style="background-color:#f9f9f9"><span style="color:#242424"><span style="color:#007400"># 導入必要的庫</span>
<span style="color:#aa0d91">import</span> numpy <span style="color:#aa0d91">as</span> np 
<span style="color:#aa0d91">import</span> scipy.stats <span style="color:#aa0d91">as</span> stats 
<span style="color:#aa0d91">import</span> matplotlib.pyplot <span style="color:#aa0d91">as</span> plt <span style="color:#007400"># 拋硬幣次數</span>
n_flips = <span style="color:#1c00cf">100 </span>
<span style="color:#007400"># 模擬拋硬幣（1 表示正面，0 表示反面）</span>coin_flips = np.random.binomial( <span style="color:#1c00cf">1</span> , <span style="color:#1c00cf">0.5</span> , n_flips) <span style="color:#007400"># 計算正面的次數</span>
n_heads = np.sum (coin_flips) <span style="color:#5c2699">print </span>
<span style="color:#5c2699">(</span> f <span style="color:#c41a16">"正面數量：<span style="color:#000000">{n_heads}</span> "</span> ) 
<span style="color:#007400"># 計算正面的概率</span>
p_heads = n_heads / n_flips 
<span style="color:#5c2699">print</span> ( <span style="color:#c41a16">f"估計正面的概率：<span style="color:#000000">{p_heads: <span style="color:#1c00cf">.2</span> f}</span> "</span> )</span></span></span></span>

輸出：

正面次數：51
預計正面概率：0.51

概率分布可視化

<span style="color:rgba(0, 0, 0, 0.8)"><span style="background-color:#ffffff"><span style="background-color:#f9f9f9"><span style="color:#242424"><span style="color:#007400"># 繪制二項分布</span>
n_trials = <span style="color:#1c00cf">10</span>p_success = <span style="color:#1c00cf">0.5</span>x = np.arange( <span style="color:#1c00cf">0</span> , n_trials+ <span style="color:#1c00cf">1</span> ) 
binomial_pmf = stats.binom.pmf(x, n_trials, p_success) plt.figure(figsize=( <span style="color:#1c00cf">10</span> , <span style="color:#1c00cf">5</span> )) 
plt.stem(x, binomial_pmf) 
plt.title( <span style="color:#c41a16">'二項分布 PMF'</span> ) 
plt.xlabel( <span style="color:#c41a16">'成功次數'</span> ) 
plt.ylabel( <span style="color:#c41a16">'概率'</span> ) 
plt.show()</span></span></span></span>

生成：

示例：硬幣翻轉的貝葉斯推理

我們將使用貝葉斯推理來估計有偏差的硬幣出現正面的概率。

先前的信念

假設 Beta 先驗分布的參數為 α = 2 和 β = 2，表示統一的先驗信念。

<span style="color:rgba(0, 0, 0, 0.8)"><span style="background-color:#ffffff"><span style="background-color:#f9f9f9"><span style="color:#242424"><span style="color:#007400"># 定義先驗分布</span>
alpha_prior = <span style="color:#1c00cf">2</span>beta_prior = <span style="color:#1c00cf">2</span>Prior = stats.beta(alpha_prior, beta_prior) <span style="color:#007400"># 繪制先驗分布</span>
x = np.linspace( <span style="color:#1c00cf">0</span> , <span style="color:#1c00cf">1</span> , <span style="color:#1c00cf">100</span> ) 
plt.figure(figsize=( <span style="color:#1c00cf">10</span> , <span style="color:#1c00cf">5</span> )) 
plt.plot(x, Prior.pdf(x), label= <span style="color:#c41a16">'Prior'</span> ) 
plt.title( <span style="color:#c41a16">'Prior Distribution'</span> ) 
plt.xlabel( <span style="color:#c41a16">'Probability of Heads'</span> ) 
plt.ylabel( <span style="color:#c41a16">'Density'</span> ) 
plt.legend() 
plt.show()</span></span></span></span>

生成：

似然和后驗

使用觀察到的數據（證據）更新先驗以獲得后驗分布。

<span style="color:rgba(0, 0, 0, 0.8)"><span style="background-color:#ffffff"><span style="background-color:#f9f9f9"><span style="color:#242424"><span style="color:#007400"># 觀察到的正面和反面的數量</span>
n_heads = <span style="color:#1c00cf">7</span>n_tails = <span style="color:#1c00cf">3 </span><span style="color:#007400"># 更新后驗分布</span>
alpha_posterior = alpha_prior + n_heads 
beta_posterior = beta_prior + n_tails 
posterior = stats.beta(alpha_posterior, beta_posterior) <span style="color:#007400"># 繪制后驗分布</span>
plt.figure(figsize=( 
<span style="color:#1c00cf">10</span> , <span style="color:#1c00cf">5</span> )) 
plt.plot(x, Prior.pdf(x), label= <span style="color:#c41a16">'Prior'</span> ) 
plt.plot(x, posterior.pdf(x), label= <span style="color:#c41a16">'Posterior'</span> , linestyle= <span style="color:#c41a16">'--'</span> ) 
plt.title( <span style="color:#c41a16">'先驗和后驗分布'</span> ) 
plt.xlabel( <span style="color:#c41a16">'正面的概率'</span> ) 
plt.ylabel( <span style="color:#c41a16">'密度'</span> ) 
plt.legend() 
plt.show()</span></span></span></span>

生成：