目錄
摘要
“右移”現象
beta分布及其小波
實驗
《Rethinking Graph Neural Networks for Anomaly Detection》,這是一篇關于圖(graph)上異常節點診斷的論文。
論文出處:ICML 2022
論文地址:Rethinking Graph Neural Networks for Anomaly Detectionhttps://arxiv.org/pdf/2205.15508https://arxiv.org/pdf/2205.15508https://arxiv.org/pdf/2205.15508https://arxiv.org/pdf/2205.15508https://arxiv.org/pdf/2205.15508![]() https://arxiv.org/pdf/2205.15508
https://arxiv.org/pdf/2205.15508
代碼地址:squareRoot3/Rethinking-Anomaly-Detection: "Rethinking Graph Neural Networks for Anomaly Detection" in ICML 2022https://github.com/squareRoot3/Rethinking-Anomaly-Detectionhttps://github.com/squareRoot3/Rethinking-Anomaly-Detectionhttps://github.com/squareRoot3/Rethinking-Anomaly-Detectionhttps://github.com/squareRoot3/Rethinking-Anomaly-Detectionhttps://github.com/squareRoot3/Rethinking-Anomaly-Detection![]() https://github.com/squareRoot3/Rethinking-Anomaly-Detection
https://github.com/squareRoot3/Rethinking-Anomaly-Detection
摘要
圖神經網絡被廣泛應用于圖的異常檢測。選擇合適的譜濾波器是圖神經網絡設計的關鍵部分之一,我們從圖譜的視角邁出了異常分析的第一步。我們的一個重要發現是,異常的存在會導致“右移”的現象,即光譜能量分布在低頻的集中度降低,而在高頻上的集中度增加。這一事實激勵我們提出beta小波圖神經網絡(BWGNN)。BWGNN具有在圖譜和空間中局部化的帶通濾波器,以更好地處理異常中的“右移”現象。我們展示了BWGNN在四個大規模數據集上的有效性。
“右移”現象
最有意思的是本文提出的右移現象,這也是文章所述的motivation,那么右移現象到底是什么呢?
考慮一個圖,有N個節點,編號從0到N-1,其拉普拉斯矩陣為L,很容易得到一般拉普拉斯的計算公式:
其中,D是圖的度矩陣,A是鄰接矩陣,這里我們只考慮無向無權圖,邊僅僅只反映圖的結構,不做他用,那么圖的度矩陣自然和圖的出度矩陣以及入度矩陣相等,并且還是個對角矩陣,此外,D和A都是對稱矩陣。
另外,上述的拉普拉斯矩陣的表達式是非規范化的,這導致其特征值的范圍不受控制,因此給出規范化的拉普拉斯矩陣計算方式:
規范化拉普拉斯矩陣能夠保證所有的特征值都在[0,2]內。
假設規范化拉普拉斯矩陣的特征值為,并且對應的正交的特征向量為
。注意這里將所有特征值從小到大排列,并且對應的特征向量也要跟隨其對應的特征值排列。
假設圖上所有節點的某一個信號為
,其中x1,x2等等都為Nx1的向量,整個信號矩陣x為NxL的shape。那么定義
為圖上針對x的傅里葉變換,注意變換之后的shape仍然為NxL。
在這里,由于拉普拉斯矩陣的特征值所對應的特征向量在一開始的特征向量矩陣U中的按列排布的,但在這里做圖傅里葉變換的時候對U做了轉置,因此可以視為從上至下,按行對應,即的第一列對應最小的特征值
,第二列對應倒數第二小的特征值
,直到最后一行對應最大的特征值
。對于做了傅里葉變換之后的
也可以從上至下如此按行看待,并且對應地,
每行也可以對應相應的特征值(畢竟是從
算過來的)(個人感覺論文里這種按列的表述有點問題,并且文章里面x的元素個數也是N,讓人難以區分單個節點上的特征向量的元素數目和圖上的節點數到底有沒有關系,有一定誤導性)。
那么接下來,注意文章中給出來的這個式子:

這個公式是論文給出用以計算圖譜能量的,聯系到之前摘要里說到異常的存在會導致圖譜能量分布在低頻減少高頻增加的說法,可以看出這是一個關鍵的量,那么他是如何反映“右移”的呢?
仔細看上面的公式,分為分母和分子兩個部分,分子指的是之前計算的圖傅里葉變換的結果中每個標量元素的平方之和,換言之,分母是
中NxL個元素的平方和,最后得到的也是一個標量。
而分子,還記得我們之前提到的從上至下每行能夠對應規范化拉普拉斯矩陣從小到大的相應的特征值的說法嗎?分子自然就是單個行(N個元素)中元素的平方之和,這樣計算出來的整個分式,對應的是相應行所對應的特征值。例如,分母是之前所提到的
所有元素平方和,而分子是
第一行中所有元素的平方和,那么這樣計算出來的圖譜能量對應的是規范化拉普拉斯矩陣的最小的特征值。
然后將所有的特征值從小到大放到橫軸上,所有對應特征值的圖譜能量放到縱軸上,就可以畫出一個圖的圖譜能量分布了。

上圖就是文章中給出的,不同規模的異常分布下的圖譜能量分布,可以看到,隨著圖的異常規模的增大,其圖譜能量的分布往高頻方向(也即特征值更大的方向)發展。
beta分布及其小波
然后就輪到我們的主角的出場了,論文本身是借鑒了Hammond的圖小波理論,通過自己構造小波,從而做出一個濾波器,然后可以對圖本身進行濾波,考慮到濾波器實際上是由一組小波構成的,因此不同的帶通的濾波器能夠過濾不同的圖的頻段上的信息,而又根據前文所述的隨著異常規模的增大圖譜能量分布的右移,因此不同的帶通濾波器基本能夠找出所有情況下的異常能量分布部分,從而確定異常。
論文首先介紹了下Hammond的圖小波理論,有一個母小波,并且這個母小波是后續一組小波的基礎,定義為
,那么在一個圖信號
上應用對應的小波
可以表示為:
其中,為圖的規范化拉普拉斯矩陣的特征值矩陣,是一個對角矩陣,并且對角線上的元素按大小排列,
是一個核函數,其定義域在
之間,并且
。此外,Hammond的圖小波理論還要滿足兩個條件:
- 根據Parseval定理,小波變換需要滿足有限性的條件:
。這意味著
,并且在頻域上表現得像個帶通濾波器。
- 小波變換通過不同尺度的帶通濾波器
覆蓋不同的頻段。
此外,為了避免圖拉普拉斯矩陣的特征值分解(以加快速度),核函數必須是一個多項式函數,即在大多數文獻之中都有
。
介紹完了Hammond的圖小波理論,接下來看看文章里是如何使用beta分布來構造他自己的小波變換的。
beta分布是個計算機視覺里用的挺多的分布,其概率密度函數如下所示:

其中,并且
是個常數。規范化拉普拉斯矩陣L的特征值滿足
,和上面beta分布里的[0,1]不同,因此做點改造,文章里用
來覆蓋[0,2]的范圍,并且進一步添加約束
來確保
是個多項式。因此,所構建的beta小波變換
可以表示為:
?令p+q=C為一個常數,那么所構造的beta小波變換一共就有C+1個beta小波:
其中,是個低通濾波器,其他的都是不同尺度的帶通濾波器。此外,當p>0的時候,核函數
滿足:
因此也滿足前述的Hammond理論的條件。
最后整體講一下他的神經網絡結構吧,首先是圖上的特征進入到MLP簡單過一遍,然后送到之前說的beta小波變換里,用C+1個濾波器過一遍(注意這個地方其實不涉及到參數的訓練,諸如C等超參數是在訓練之前就確定好了的,換言之,beta小波變換實際上不涉及到神經網絡里參數的訓練),得到C+1個新的特征,將這些特征簡單的按列拼接到一起,然后送入MLP分類,輸出一個兩個元素的向量,做了softmax后可以視為概率,其中索引為1的元素為該節點為異常節點的概率。
最后,光有概率還不行,這種二分類問題需要一個閾值來判斷的,那么怎么找這個閾值呢,文章的代碼里面給的方法是,將數據集分為訓練集/驗證集/測試集三個部分,使用訓練集進行訓練,然后遍歷[0,1]里的元素,以一定的步長,這個遍歷的值作為當前的概率閾值,在驗證集上測試,當使用當前概率閾值的時候,算出來的F1指標如何,最終選擇F1指標最大的那個情況所對應的概率閾值作為最終的概率閾值,最后,在測試集上使用之前選好的概率閾值檢驗在測試集上的性能效果。
實驗
最后簡單看下實驗部分吧,其實這種文章發出來他自己的的性能效果肯定基本上都要好于他拿出來作比較的方法的(2333),下面是文章中給的性能對比表格。


順便看了下參數C對性能的影響。

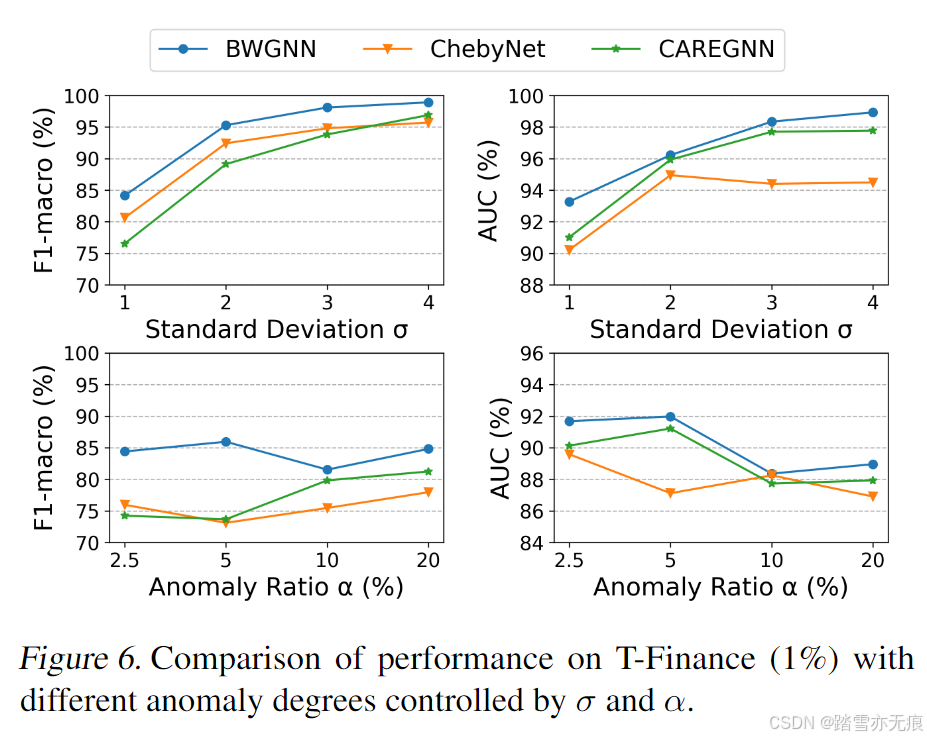
最后還比較了下不同異常程度下的性能表現。

)
)



)












