目錄
簡介:
遞歸問題解題的思路模板
例題1:漢諾塔
例題2:合并兩個有序鏈表
例題3:反轉鏈表
例題4:兩兩交換鏈表中的節點
例題5:Pow(x,n)-快速冪
結語:
簡介:
本系列將會帶大家深入理解搜索中的一大分支深搜,深搜是離不開遞歸的和回溯思想的(優化需要剪枝),故我會在例題中詳細指出解決這一系列問題的思考思路和解題技巧。
那么我們就從遞歸開始(深搜的基礎)也就是本文中主要介紹的。
什么是遞歸?
簡單來說就是函數自己調用自己。
為什么會用到遞歸?
大問題可以拆解成相同的子問題,且子問題的解法和大問題的一模一樣,這是就可以用到遞歸。

在解決?個規模為n的問題時,如果滿?以下條件,我們可以使用遞歸來解決:
a. 問題可以被劃分為規模更?的?問題,并且這些?問題具有與原問題相同的解決?法。
b. 當我們知道規模更?的?問題(規模為n-1)的解時,我們可以直接計算出規模為n的問題的解。
c. 存在?種簡單情況,或者說當問題的規模?夠?時,我們可以直接求解問題。
?般的遞歸求解過程如下:
a. 驗證是否滿?簡單情況。
b. 假設較?規模的問題已經解決,解決當前問題。
上述步驟可以通過數學歸納法來證明。
如何理解遞歸?
不要太在意細節,相信函數。?
遞歸問題解題的思路模板
當然在設計遞歸函數之前最重要的是你要你的遞歸函數干嘛。
1.遞歸函數的作用
2.相同子問題------------函數頭
3.只關心某一個子問題是如何解決的------------函數體
4.遞歸出口
建議友友在寫遞歸類型的題目是一定要把這三個地方考慮清楚了再下手。
最后就是相信函數。
例題1:漢諾塔
鏈接:漢諾塔
題目簡介:
遞歸問題非常經典的一道題目,在經典漢諾塔問題中,有 3 根柱子及 N 個不同大小的穿孔圓盤,盤子可以滑入任意一根柱子。一開始,所有盤子自上而下按升序依次套在第一根柱子上(即每一個盤子只能放在更大的盤子上面)。移動圓盤時受到以下限制:
(1) 每次只能移動一個盤子;
(2) 盤子只能從柱子頂端滑出移到下一根柱子;
(3) 盤子只能疊在比它大的盤子上。
請編寫程序,用棧將所有盤子從第一根柱子移到最后一根柱子。

解法:
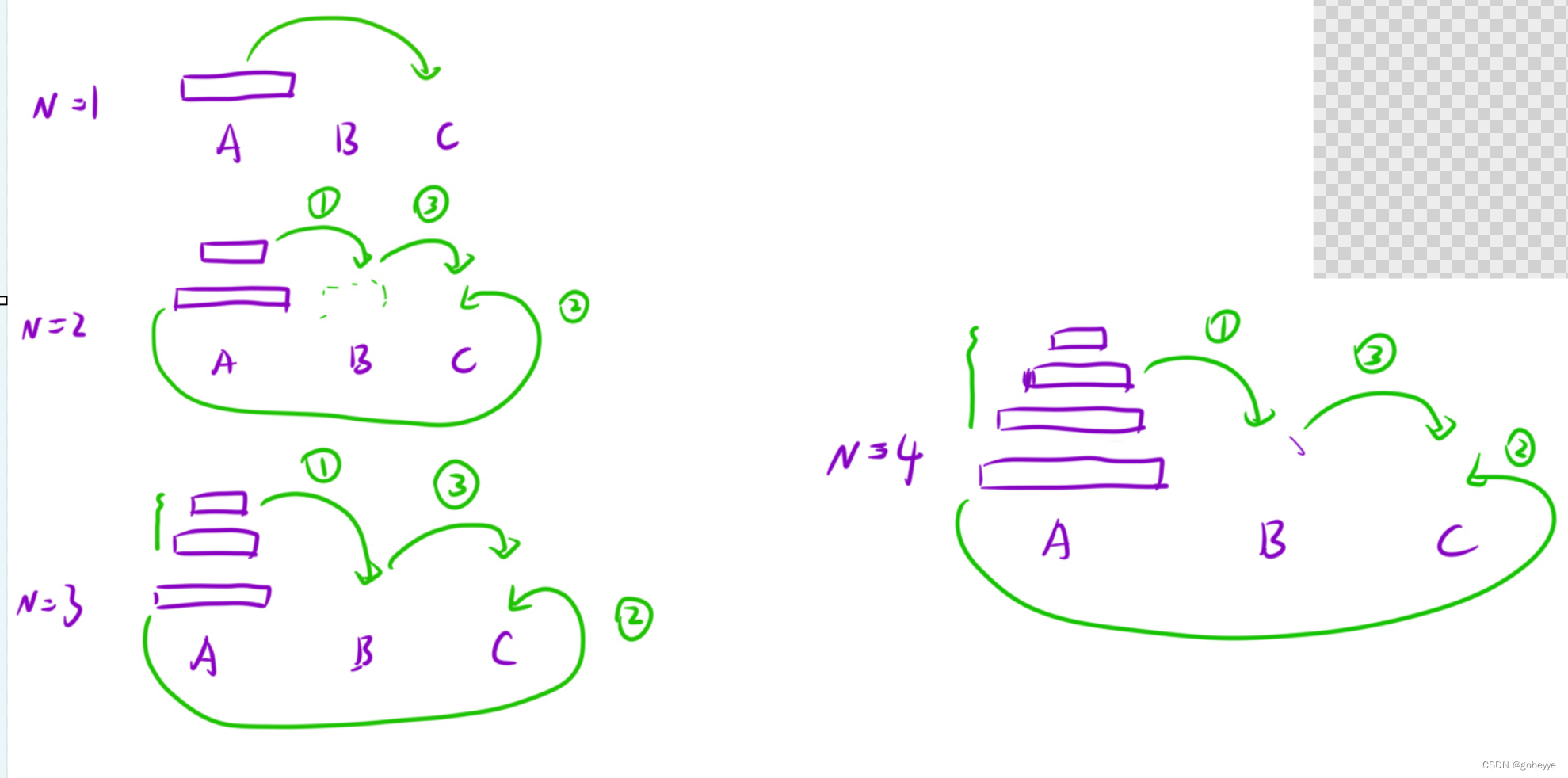
我們可以看到每次都可以把大問題分解成相同的子問題,且子問題的解決方法和大問題的一模一樣故我們可以使用遞歸來處理。?
1.遞歸函數的作用
函數作?:將A中的上?n個盤?挪到C中。這里的A和C是函數參數的A和C不是實際的(很重要)。
2.相同子問題(函數頭)
我們要設計一個函數頭來完成漢諾塔的遞歸過程,我們可以看到我們需要三根柱子和要記錄下來還剩下幾個盤子。故我們的函數頭可以設計成public void dfs(List<Integer>?a, List<Integer> b, List<Integer> c, int n)。關于List<Integer>如果友友還沒有學到的話可以把他看成一個數組。
3.只關心某一個子問題是如何解決的(函數體)
我們取第三層漢諾塔來研究(大問題被拆成3層漢諾塔)。
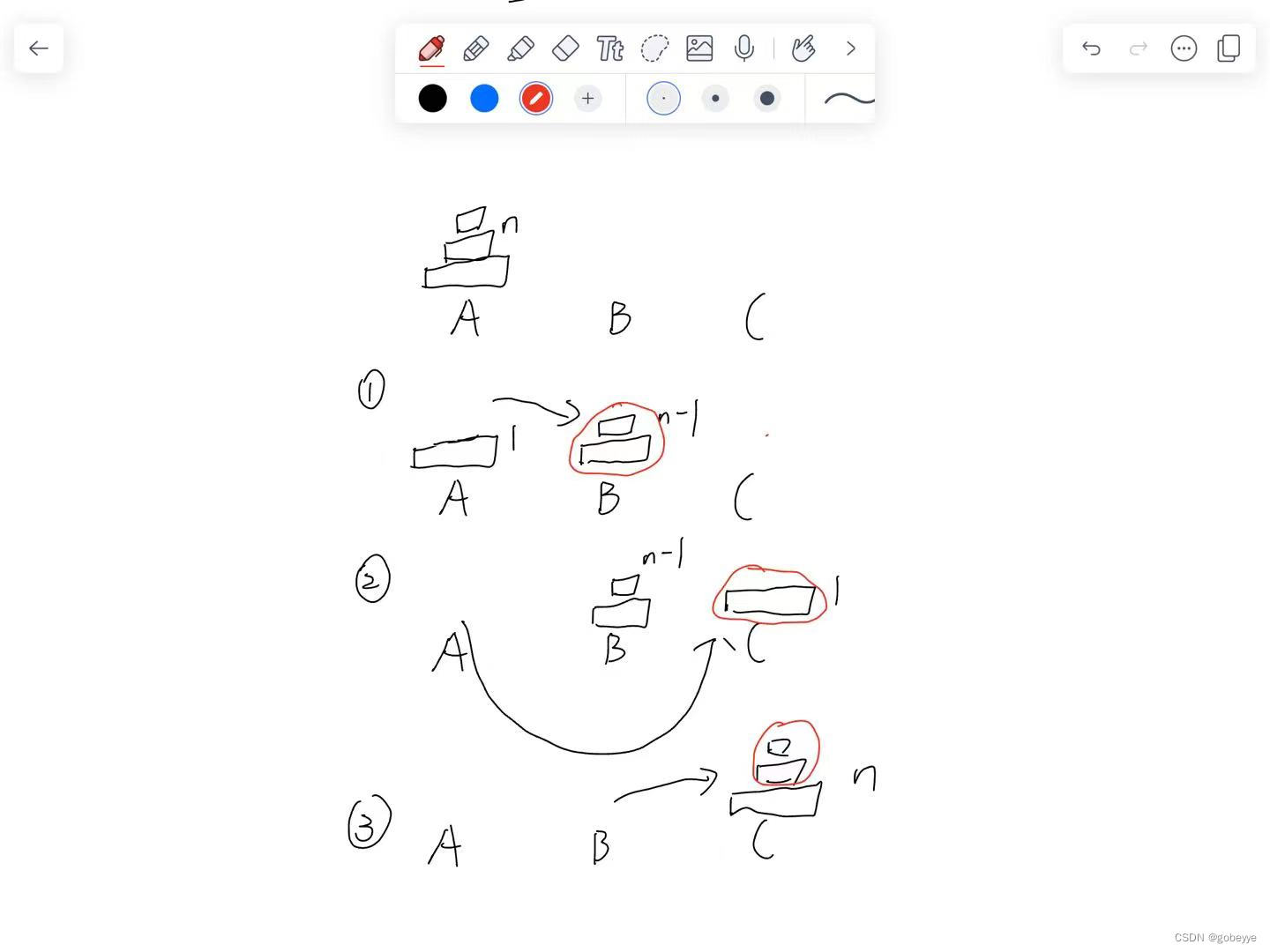
我們發現子問題剛來三件事
1.把A上面n - 1 個盤子通過C移動到B?
2.把A上面最后一個盤中移動到C
3.把B上面n - 1個盤中通過A 移動到C
dfs(a, c, b, n - 1);
c.add(a.remove(a.size() - 1));//這里是因為給出的例題這樣做就是把盤中從A移動到C(理解思路即可)
dfs(b, a, c, n - 1);
4.遞歸出口
當問題的規模變為n=1時,即只有?個盤?時,我們可以直接將其從A柱移動到C柱。
本例題代碼實現如下:
class Solution {public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {dfs(A,B,C,A.size());}public void dfs(List<Integer> A, List<Integer> B, List<Integer> C,int n ){if(n == 1){C.add(A.remove(A.size() - 1));return;}dfs(A,C,B,n - 1);C.add(A.remove(A.size() - 1));dfs(B,A,C,n - 1);}
}關于本例題要注意的點:c.add(a.remove(a.size() - 1));可能有的友友會糾結為什么不是remove(0)呢,其實自己模擬一下即可,我們移走盤子是從最上面那個盤子開始移動的。
不用太深究函數的細節(陷入將無法自拔),如果是第一次的話可以去b站上看看遞歸的全過程細節(這里的不用深究是建立在已經對它的展開有一定理解了,第一次學漢諾塔的話我還是建議大家可以看看別人推的整個過程,理解更加深刻)。
例題2:合并兩個有序鏈表
鏈接:合并兩個有序鏈表
題目簡介:
將兩個升序鏈表合并為一個新的?升序?鏈表并返回。新鏈表是通過拼接給定的兩個鏈表的所有節點組成的。?
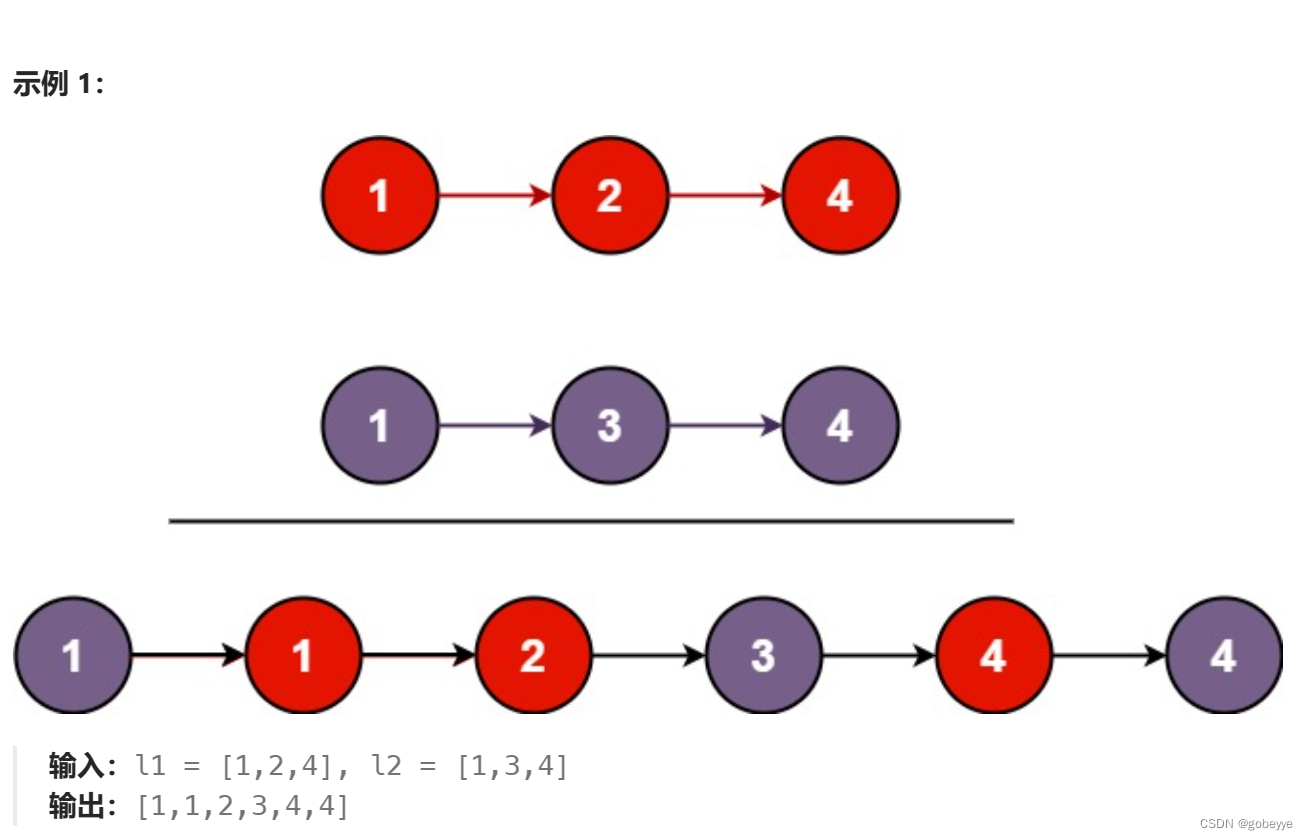
解法:
通過分析題目我們發現可以把大問題拆成下圖的子問題,上面的1已經合并有序現在要讓2,4和下面鏈表合并有序。
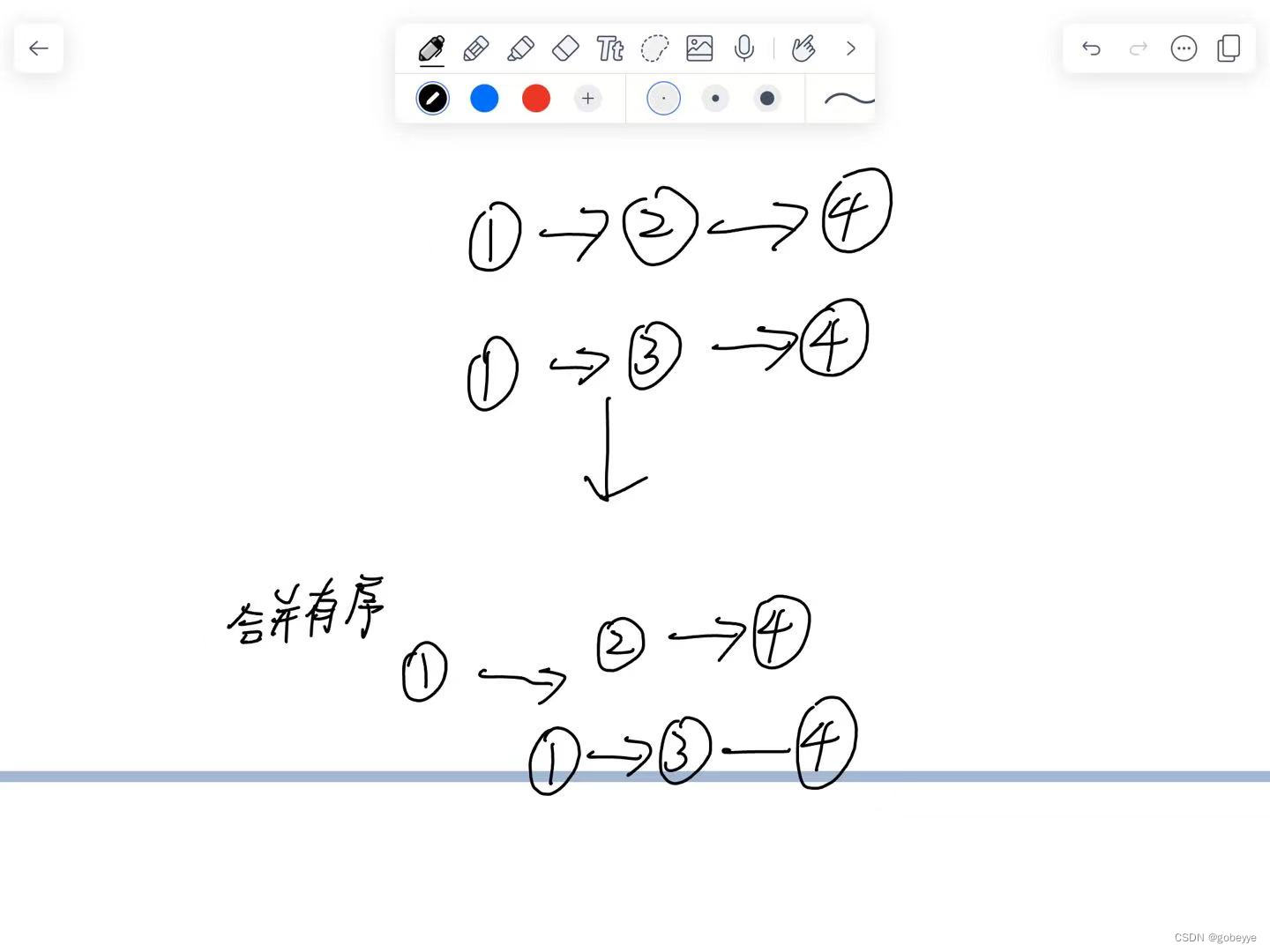
故我們可以用遞歸來解決這道問題。
1.遞歸函數的作用
交給你兩個鏈表的頭結點,你幫我把它們合并起來,并且返回合并后的頭結點.
2.相同子問題(函數頭)
由上圖可以看到函數要包含兩個鏈表還要能返回合并后的鏈表故函數頭設定為:public ListNode mergeTwoLists(ListNode l1, ListNode l2)
3.只關心某一個子問題是如何解決的(函數體)
選擇兩個頭結點中較小的結點作為最終合并后的頭結點,然后將剩下的鏈表交給遞歸函數去處理。
4.遞歸出口
當某?個鏈表為空的時候,返回另外?個鏈表。
代碼如下:
class Solution {public ListNode mergeTwoLists(ListNode list1, ListNode list2) {if(list1 == null){return list2;}if(list2 == null){return list1;}if(list1.val <= list2.val){list1.next = mergeTwoLists(list1.next,list2);return list1;}else{list2.next = mergeTwoLists(list1,list2.next);return list2;}}
}例題3:反轉鏈表
鏈接:反轉鏈表
題目簡介:
給你單鏈表的頭節點?head?,請你反轉鏈表,并返回反轉后的鏈表。
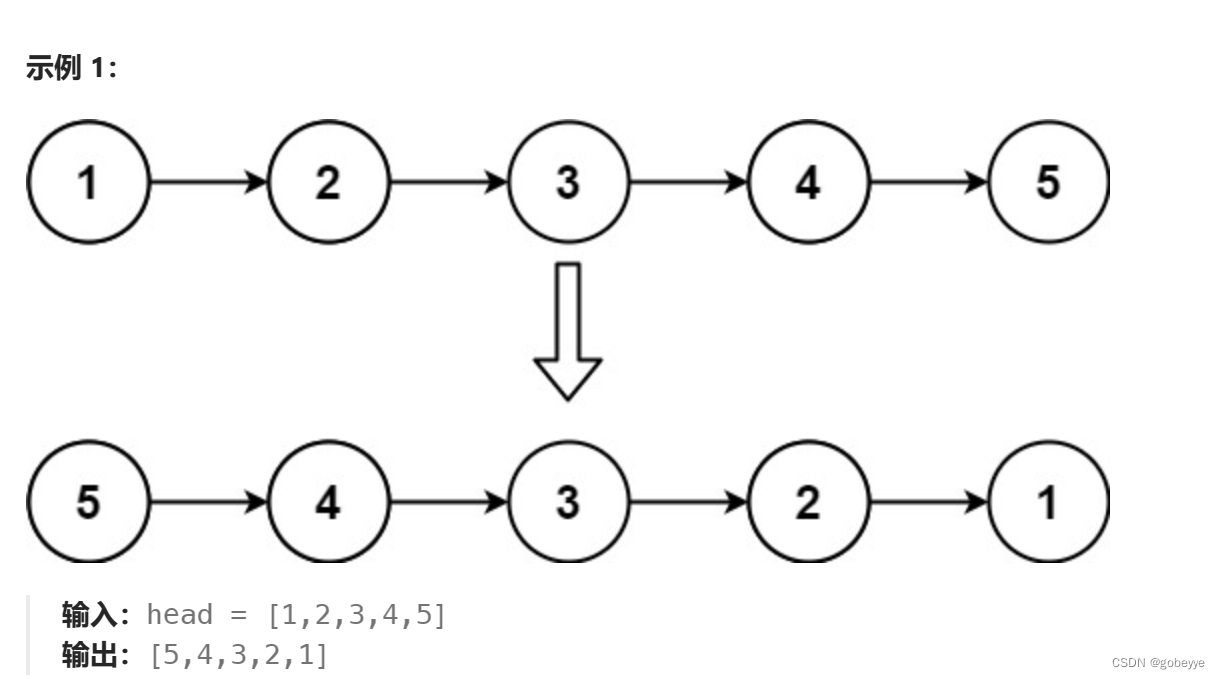
解法:
要想讓1到5逆序,可以讓5逆序后讓1到4逆序一直這樣下去我們不難發現這就是遞歸。
1.遞歸函數的作用
交給你?個鏈表的頭指針,你幫我逆序之后,返回逆序后的頭結點。
2.相同子問題(函數頭)
需要傳入鏈表,5節點逆序后要把逆序后的新頭節點返回故將函數體設為public ListNode reverseList(ListNode head)
3.只關心某一個子問題是如何解決的(函數體)
先把當前結點之后的鏈表逆序,逆序完之后,把當前結點添加到逆序后的鏈表后?即可。
4.遞歸出口
當前結點為空或者當前只有?個結點的時候,不?逆序,直接返回。
代碼如下:
class Solution {public ListNode reverseList(ListNode head) {ListNode newHead = head;if(head == null){return head;}ListNode cur = head.next;ListNode prev = head;head.next = null;while(cur != null){ListNode next = cur.next;cur.next = prev;prev = cur;cur = next;}return prev;}
}例題4:兩兩交換鏈表中的節點
鏈接:兩兩交換鏈表中的節點
題目簡介:
給你一個鏈表,兩兩交換其中相鄰的節點,并返回交換后鏈表的頭節點。你必須在不修改節點內部的值的情況下完成本題(即,只能進行節點交換)。
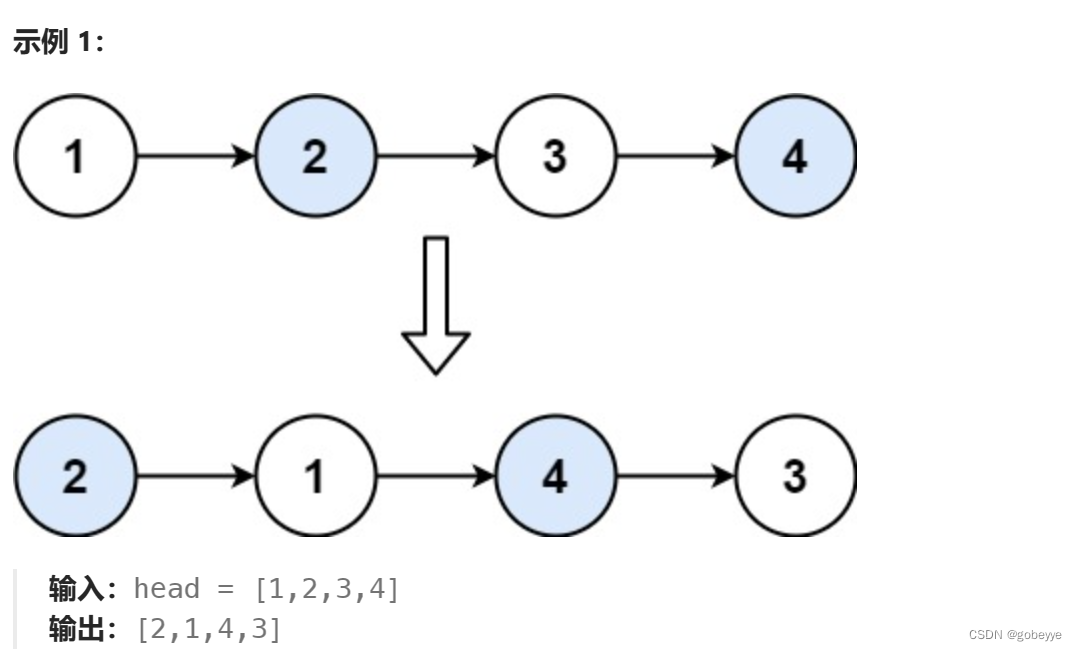
?解法:
我們通過閱讀題目可以發現要使整個鏈表兩兩交換?,可以將大問題分為把1和2后面的節點兩兩交換,把一二交換即可,同理3和4也是同樣的處理思路。
1.遞歸函數的作用
交給你?個鏈表,將這個鏈表兩兩交換?下,然后返回交換后的頭結點;
2.相同子問題(函數頭)
需要傳入原始鏈表和返回新的頭節點故設計為:public ListNode swapPairs(ListNode head)
3.只關心某一個子問題是如何解決的(函數體)
先去處理?下第?個結點往后的鏈表,然后再把當前的兩個結點交換?下,連接上后面處理后的鏈表;
4.遞歸出口
當前結點為空或者當前只有?個結點的時候,不?交換,直接返回。
代碼如下:
class Solution {public ListNode swapPairs(ListNode head) {if(head == null || head.next == null){return head;}ListNode newHead = head.next;head.next = swapPairs(head.next.next);newHead.next = head;return newHead;}
}例題5:Pow(x,n)-快速冪
鏈接:Pow(x,n)
題目簡介:
實現?pow(x,?n)?,即計算?x?的整數?n?次冪函數(即,xn?)。

??解法:
這題不能使用1個1個數的分離遞歸(會超時),我們這里要采用二分的思路,具體實現如下:
1.遞歸函數的作用
求出x 的n 次?是多少,然后返回;
2.相同子問題(函數頭)
需要傳入需要n次方的x和n還要將其返回public double pow(double x, int n)
3.只關心某一個子問題是如何解決的(函數體)
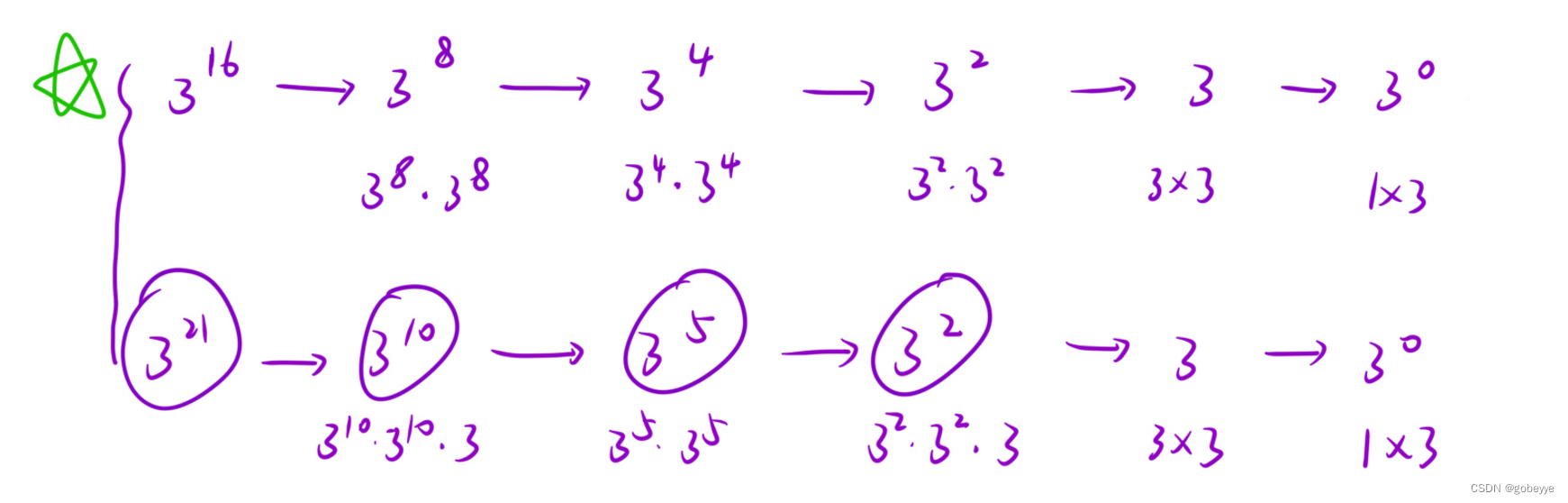
先求出x 的n / 2 次?是多少,然后根據n 的奇偶,得出x 的n 次?是多少;
4.遞歸出口
當n 為0 的時候,返回1 即可。
代碼如下:
最上面要區分一下正負數的區別即可。
class Solution {public double myPow(double x, int n) {return (n < 0) ? 1.0 / pow(x, - n) : pow(x , n);}public double pow(double x,int n){if(n == 0){return 1.0;}double tmp = pow(x,n / 2);return (n % 2 == 0) ? tmp * tmp : tmp * tmp * x;}
}總結:本文章是搜索回溯的第一篇,帶大家再復習了一下遞歸,后續的章節會帶領大家深度理解深搜和回溯算法。
結語:
其實寫博客不僅僅是為了教大家,同時這也有利于我鞏固自己的知識點,和一個學習的總結,由于作者水平有限,對文章有任何問題的還請指出,接受大家的批評,讓我改進,如果大家有所收獲的話還請不要吝嗇你們的點贊收藏和關注,這可以激勵我寫出更加優秀的文章。






)
)
)






——二叉樹+二叉樹層次遍歷+二叉搜索樹)


)
