布隆過濾器
問題前景:
之前學習了位圖,我們知道位圖在大量數據查找時候是很方便的。但位圖的缺陷在于只能用于整型數據。而在實際中,我們的數據更多的是更復雜的字符串或者自定義類型。那么此時位圖就顯得有點無力,所以就誕生了叫布隆過濾器的數據結構。
布隆過濾器:
布隆過濾器(Bloom Filter)是一種空間效率極高的概率型數據結構,主要用于快速判斷一個元素是否“可能存在于”一個集合中,或者“絕對不存在于”集合中。

那可能會有疑問,為什么布隆過濾器需要映射多個值,而不只映射單個值呢?

假設我們現在需要查找名字為胡歌,此時就存在Hash沖突,胡歌明明沒有插入數據,但顯示已經在布隆過濾器里了,存在誤判。

而我們使用多個Hash函數進行分別插入,雖然不能完全解決這個問題,但是可以大大降低誤判率。
在映射的K個位置里,只要有其中一個不在,該元素就是不存在。
只有映射的K個位置里,全部在,才可能在(存在誤判風險)。
布隆過濾器理論結論:
布隆過濾器的推到,這里小編就不細講了,大家有興趣可以自行搜索。小編就簡單說下結論
當哈希函數固定時,插入的數據增加,誤判率增加。開的比特位增加,誤判率就減少。
判斷一個數不在是準確的,判斷一個數在是不準確的。
布隆過濾器代碼實現:
#pragma once
#include<iostream>
#include<vector>
#include<string>using namespace std;template<size_t size>
class BitMap
{
public:BitMap(){_bm.resize(size);}void set(size_t x){int i = x / 32;int j = x % 32;_bm[i] |= (1 << j);}bool test(size_t x){int i = x / 32;int j = x % 32;return _bm[i]&(1 << j);}private:vector<size_t> _bm;
};struct HashFuncBKDR
{size_t operator()(const string& s){size_t hash = 0;for (auto ch : s){hash *= 31;hash += ch;}return hash;}
};
struct HashFuncAP
{size_t operator()(const string& s){size_t hash = 0;for (size_t i = 0; i < s.size(); i++){if ((i & 1) == 0) {hash ^= ((hash << 7) ^ (s[i]) ^ (hash >> 3));}else {hash ^= (~((hash << 11) ^ (s[i]) ^ (hash >>5)));}}return hash;}
};
struct HashFuncDJB
{size_t operator()(const string & s){size_t hash = 5381;for (auto ch : s){hash = hash * 33 ^ ch;}return hash;}
};template<size_t N, size_t X = 5, class K=string,class Hash1= HashFuncBKDR,class Hash2= HashFuncAP,class Hash3= HashFuncDJB>
class Blomm_fiter
{
public:void set(const K&key){size_t hash1 = Hash1()(key) % M;size_t hash2 = Hash2()(key) % M;size_t hash3 = Hash3()(key) % M;_bm.set(hash1);_bm.set(hash2);_bm.set(hash3);}bool test(const K&key){size_t hash1 = Hash1()(key) % M;size_t hash2 = Hash2()(key) % M;size_t hash3 = Hash3()(key) % M;if(!_bm.test(hash1)){return false;}if (!_bm.test(hash2)){return false;}if (!_bm.test(hash3)){return false;}return true;//不一定準確}// 獲取公式計算出的誤判率double getFalseProbability(){double p = pow((1.0 - pow(2.71, -3.0 / X)), 3.0);return p;}private:static const size_t M = N * X; //M為實際需要開的數據BitMap<M> _bm;
};代碼解釋:
類模板定義:
N為傳入的數據大小,X為倍數,用于求出M,K為模板類型,剩下的就是哈希函數。這里為了簡單實現,就寫死哈希函數,在實際實現中,哈希函數可以進行動態調整多少。
成員變量:
M需要開多少個比特位
_bm就是普通位圖,因為布隆過濾器或許還是會轉成int類型進行映射。我們這里直接套用即可。
Set(size_t x)
使用多個哈希函數求出映射的位置,并調用_bm的函數set進行置1
Test(size_t x)
該函數為布隆過濾器核心,當有一個不在就是不在,這個是準確的。當全部在的時候可能在,這個是不準確的。
測試代碼:

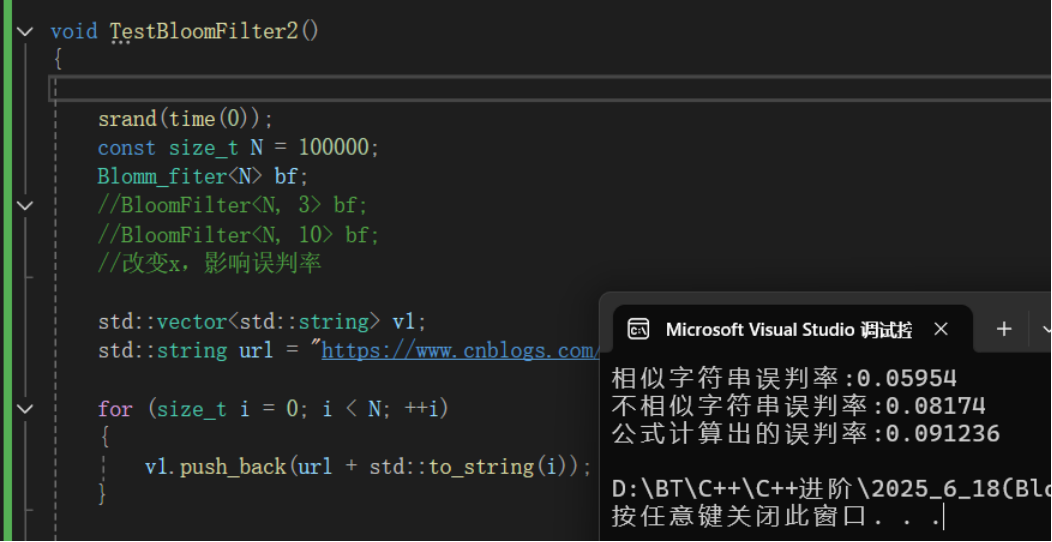

通過測試代碼,就能很直觀的看出,我們可以通過控制X(倍數)的大小,進行控制誤判率。X越小誤判率越大,X越大誤判率越小。
布隆過濾器的實際應用:
布隆過濾器的優勢(空間小、查詢快、“不存在”判斷準)使其非常適合用于需要快速過濾掉大量“肯定不存在”的請求的場景,尤其當數據量巨大且對少量誤判可以容忍時: ?
緩存穿透防護: ?
問題:查詢一個不存在的數據,導致請求繞過緩存直接沖擊底層數據庫(如Redis、MySQL)。 ?
解決:將所有可能存在的緩存鍵(或數據庫主鍵)放入布隆過濾器。查詢時先查布隆過濾器:
若返回“不存在”,則直接返回空或錯誤,避免查數據庫。 ?
若返回“可能存在”,再去查緩存/數據庫。即使有少量誤判(查了數據庫但沒結果),也比所有不存在請求都查數據庫要好得多。 ?
網絡爬蟲的URL去重: ?
問題:避免重復抓取同一個URL。 ?
解決:將已抓取或計劃抓取的URL放入布隆過濾器。
新URL來臨時: ?
查布隆過濾器:若返回“不存在”,則一定是新URL,加入抓取隊列并添加到過濾器。 ?
若返回“可能存在”,則大概率是重復URL(即使有小概率誤判是新URL,放棄抓取也是可以接受的代價)。 ?











)


:移動應用核心指標解析與用戶分層營收策略)



)
