LeetCode 455 分發餅干

題目描述

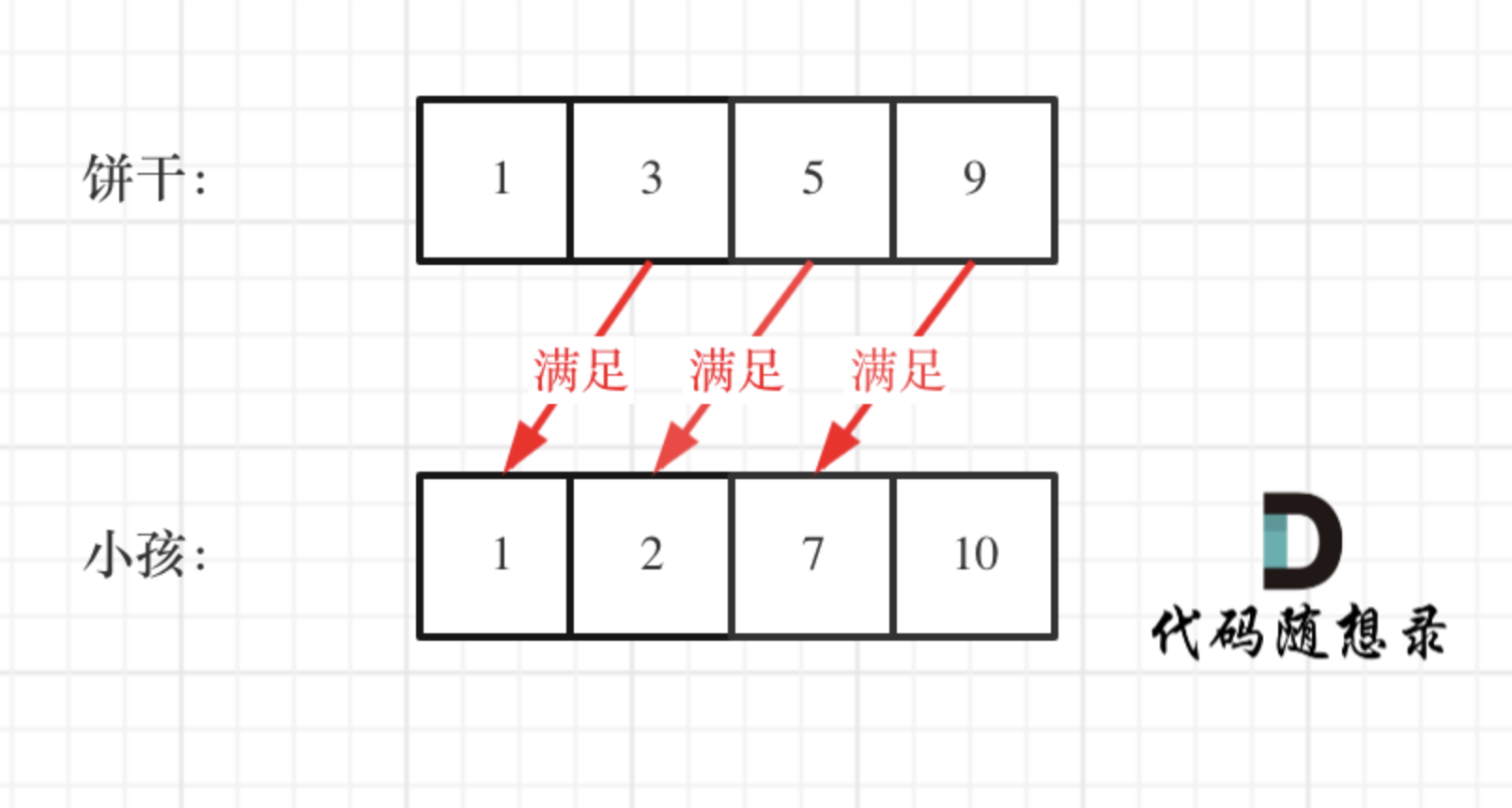
假設你是一位很棒的家長，想要給你的孩子們一些小餅干。但是，每個孩子最多只能給一塊餅干。

對每個孩子?i，都有一個胃口值?g[i]，這是能讓孩子們滿足胃口的餅干的最小尺寸；并且每塊餅干?j，都有一個尺寸?s[j]?。如果?s[j]?>= g[i]，我們可以將這個餅干?j?分配給孩子?i?，這個孩子會得到滿足。你的目標是盡可能滿足越多數量的孩子，并輸出這個最大數值。

示例?1:

輸入: g = [1,2,3], s = [1,1]
輸出: 1
解釋: 
你有三個孩子和兩塊小餅干，3個孩子的胃口值分別是：1,2,3。
雖然你有兩塊小餅干，由于他們的尺寸都是1，你只能讓胃口值是1的孩子滿足。
所以你應該輸出1。

示例?2:

輸入: g = [1,2], s = [1,2,3]
輸出: 2
解釋: 
你有兩個孩子和三塊小餅干，2個孩子的胃口值分別是1,2。
你擁有的餅干數量和尺寸都足以讓所有孩子滿足。
所以你應該輸出2.

思路

????????這道題目可以先固定餅干的數量，然后找到能滿足的最大的小孩胃口，也可以先固定要滿足的小孩胃口，再找能滿足他胃口的最小餅干數量。這里我們選擇先從最大的胃口開始for循環遍歷，如果餅干數大于等于小孩的胃口，再遍歷下一個餅干，否則就一直找更小的胃口，直到胃口小于這個餅干數為止。

代碼實現

class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(),g.end());sort(s.begin(),s.end());int result = 0;int index = s.size() - 1;for(int i = g.size() - 1;i >= 0;i--){if(index >= 0 && s[index] >= g[i]){result++;index--;}}return result;}
};

LeetCode 376 擺動序列

題目描述

如果連續數字之間的差嚴格地在正數和負數之間交替，則數字序列稱為?擺動序列 。第一個差（如果存在的話）可能是正數或負數。僅有一個元素或者含兩個不等元素的序列也視作擺動序列。

• 例如，?[1, 7, 4, 9, 2, 5]?是一個?擺動序列?，因為差值?(6, -3, 5, -7, 3)?是正負交替出現的。

• 相反，[1, 4, 7, 2, 5]?和?[1, 7, 4, 5, 5]?不是擺動序列，第一個序列是因為它的前兩個差值都是正數，第二個序列是因為它的最后一個差值為零。

子序列?可以通過從原始序列中刪除一些（也可以不刪除）元素來獲得，剩下的元素保持其原始順序。

給你一個整數數組?nums?，返回?nums?中作為?擺動序列?的?最長子序列的長度?。

示例 1：

輸入：nums = [1,7,4,9,2,5]
輸出：6
解釋：整個序列均為擺動序列，各元素之間的差值為 (6, -3, 5, -7, 3) 。

示例 2：

輸入：nums = [1,17,5,10,13,15,10,5,16,8]
輸出：7
解釋：這個序列包含幾個長度為 7 擺動序列。
其中一個是 [1, 17, 10, 13, 10, 16, 8] ，各元素之間的差值為 (16, -7, 3, -3, 6, -8) 。

示例 3：

輸入：nums = [1,2,3,4,5,6,7,8,9]
輸出：2

思路

? ? ? ? 本題的基本思路是判斷與前一個數的結果<0，同時與后一個數相減的結果>0，或者反過來，就可以記錄一個峰值。

????????需要注意的細節一：如果前后的元素有平坡，這時候三個2中有一個需要記錄為峰值，但是左右兩邊始終有一邊的增長數量或者是減小數量為0，這時候就需要將判斷條件改為

nums[i] - nums[i - 1] <= 0 && nums[i + 1] - nums[i] > 0

或者

nums[i] - nums[i - 1] <= 0 && nums[i + 1] - nums[i] > 0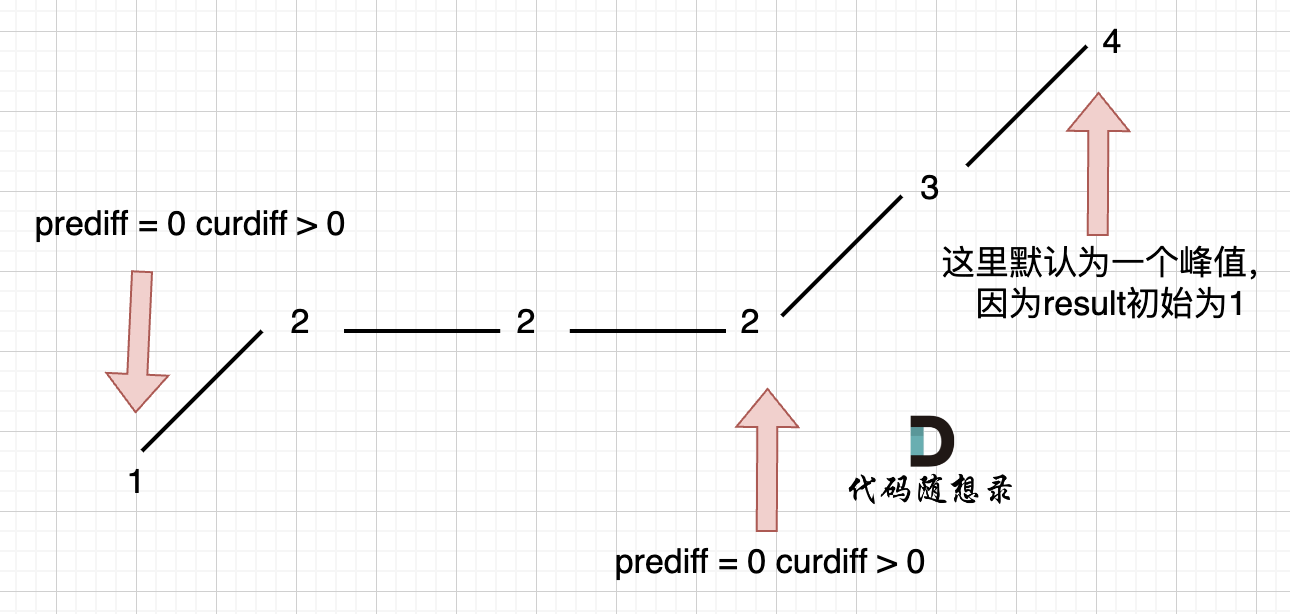

細節二：結尾默認記錄為一個峰值，同時開頭只要第二個數不和第一個數相等，就可以記錄為一個峰值。

細節三：單調有平坡的情況

例如[1,2,2,2,3,4]，如圖：

圖中，我們可以看出按照先前的思路，會在2這個地方記錄一個峰值，因為 單調中的平坡 不能算峰值（即擺動）。所以為了避免這種情況，更新prediff的條件要有變化，只有curdiff有變化的時候，才更新prediff，如果curdiff一直是平坡，那么就不更新prediff。并且因為默認了最后一個數是一個峰值，所以curdiff = 0，prediff不等于0的情況不能記錄峰值。

代碼實現

class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if(nums.size() <= 1) return nums.size();int prediff = 0;int result = 1;int curdiff = 0;for(int i = 0;i < nums.size() - 1;i++){curdiff = nums[i + 1] - nums[i];if(prediff <= 0 && curdiff > 0 || prediff >= 0 && curdiff < 0){result++;}if(curdiff != 0) prediff = curdiff;}return result;}
};

LeetCode 53 最大子序和

題目描述

給你一個整數數組?nums?，請你找出一個具有最大和的連續子數組（子數組最少包含一個元素），返回其最大和。

子數組是數組中的一個連續部分。

示例 1：

輸入：nums = [-2,1,-3,4,-1,2,1,-5,4]
輸出：6
解釋：連續子數組?[4,-1,2,1] 的和最大，為?6 。

示例 2：

輸入：nums = [1]
輸出：1

示例 3：

輸入：nums = [5,4,-1,7,8]
輸出：23

思路

本題的思路是遍歷整個數組，當子序列的和小于0時，就重新開始加和，同時每遍歷一個數，如果子序列和，大于當前result中存放的數，都要更新result的值。

代碼實現

class Solution {
public:int maxSubArray(vector<int>& nums) {int sum = 0;int result = nums[0];for(int i = 0; i < nums.size();i++){sum += nums[i];if(sum > result) result = sum;if(sum < 0) sum = 0;}return result;}
};

LeetCode 122 買賣股票的最佳時機II

題目描述

給你一個整數數組?prices?，其中?prices[i]?表示某支股票第?i?天的價格。

在每一天，你可以決定是否購買和/或出售股票。你在任何時候?最多?只能持有?一股?股票。你也可以先購買，然后在?同一天?出售。

返回?你能獲得的?最大?利潤?。

示例 1：

輸入：prices = [7,1,5,3,6,4]
輸出：7
解釋：在第 2 天（股票價格 = 1）的時候買入，在第 3 天（股票價格 = 5）的時候賣出, 這筆交易所能獲得利潤 = 5 - 1 = 4 。隨后，在第 4 天（股票價格 = 3）的時候買入，在第 5 天（股票價格 = 6）的時候賣出, 這筆交易所能獲得利潤 = 6 - 3 = 3 。總利潤為 4 + 3 = 7 。

示例 2：

輸入：prices = [1,2,3,4,5]
輸出：4
解釋：在第 1 天（股票價格 = 1）的時候買入，在第 5 天 （股票價格 = 5）的時候賣出, 這筆交易所能獲得利潤 = 5 - 1 = 4 。總利潤為 4 。

示例?3：

輸入：prices = [7,6,4,3,1]
輸出：0
解釋：在這種情況下, 交易無法獲得正利潤，所以不參與交易可以獲得最大利潤，最大利潤為 0 。

思路

這道題的思路可以簡化為和上一題類似的思路，算出每一個相鄰數的差值，只累加正數，就可以得到最大利潤。

假如第 0 天買入，第 3 天賣出，那么利潤為：prices[3] - prices[0]。

相當于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。

此時就是把利潤分解為每天為單位的維度，而不是從 0 天到第 3 天整體去考慮！

不管是哪一天購入，哪一天賣出，只要在賺了錢，將賺得的錢數累加起來，就可以得到最大的利潤。

代碼實現?

class Solution {
public:int maxProfit(vector<int>& prices) {int result = 0;for(int i = 1; i < prices.size();i++){if(prices[i] - prices[i - 1] > 0){result += prices[i] - prices[i - 1];}}return result;}
};