鏈表
- 前言
- 一、鏈表
- 1.1 鏈表的概念及結構
- 1.2 鏈表的分類
- 1.3 鏈表的實現
- 1.4 鏈表面試題
- 1.5 雙向鏈表的實現
- 二、順序表和鏈表的區別
- 三、單項鏈表實現具體代碼
- text.h
- text.c
- main.c
- 單鏈表的打印
- 空間的開辟
- 鏈表的頭插、尾插
- 鏈表的頭刪、尾刪
- 鏈表中元素的查找
- 鏈表在指定位置之前、之后插入數據
- 刪除鏈表中的結點
- 銷毀鏈表
- 四、雙向循環鏈表代碼的具體實現
- text.h
- text.c
- main.c
- 雙向循環鏈表的創建
- 雙向循環鏈表的初始化
- 雙向循環鏈表的銷毀
- 雙向循環鏈表的打印
- 雙向循環鏈表的頭插和尾插
- 雙向循環鏈表的頭刪和尾刪
- 雙向循環鏈表的元素查找
- 雙向循環鏈表的插入和刪除
前言
鏈表是一種常見的數據結構,由一系列節點組成,每個節點包含數據和指向下一個節點的指針。鏈表的一個顯著特點是,它不需要在內存中連續存儲,因此可以高效地插入和刪除節點。這種靈活性使得鏈表在許多應用中成為理想的選擇,尤其是在需要動態調整數據結構大小的場景中。
在鏈表的實現中,通常會有頭節點和尾節點之分。頭節點是鏈表的第一個節點,而尾節點是鏈表的最后一個節點。通過遍歷鏈表,我們可以訪問鏈表中存儲的所有數據。鏈表還支持在鏈表頭部或尾部快速添加新節點,這些操作的時間復雜度通常為O(1)。
然而,鏈表也有一些缺點。比如,訪問鏈表中的某個特定節點需要從頭節點開始遍歷,這導致訪問鏈表中間節點的平均時間復雜度為O(n)。此外,鏈表需要額外的空間來存儲指針,這增加了內存的使用。
鏈表有多種類型,如單向鏈表、雙向鏈表和循環鏈表等。單向鏈表是最簡單的鏈表類型,每個節點只有一個指向下一個節點的指針。雙向鏈表則允許節點同時指向前一個和下一個節點,這使得雙向鏈表在某些操作上比單向鏈表更高效。循環鏈表則是將尾節點的指針指向頭節點,形成一個閉環。
在實際應用中,鏈表常用于實現棧、隊列和哈希表等數據結構。例如,鏈表可以作為棧的底層數據結構,實現元素的先進后出。此外,鏈表還可以用于實現動態數組,支持元素的動態插入和刪除。
總之,鏈表作為一種重要的數據結構,在編程和數據處理中發揮著重要作用。盡管鏈表在某些方面存在不足,但其靈活性和高效性使得它在許多場景中仍然是理想的選擇。通過深入了解鏈表的特性和應用,我們可以更好地利用這種數據結構來解決實際問題。
一、鏈表
1.1 鏈表的概念及結構
概念:鏈表是一種物理存儲結構上非連續、非順序的存儲結構,數據元素的邏輯順序是通過鏈表
中的指針鏈接次序實現的 。

現實中 數據結構中
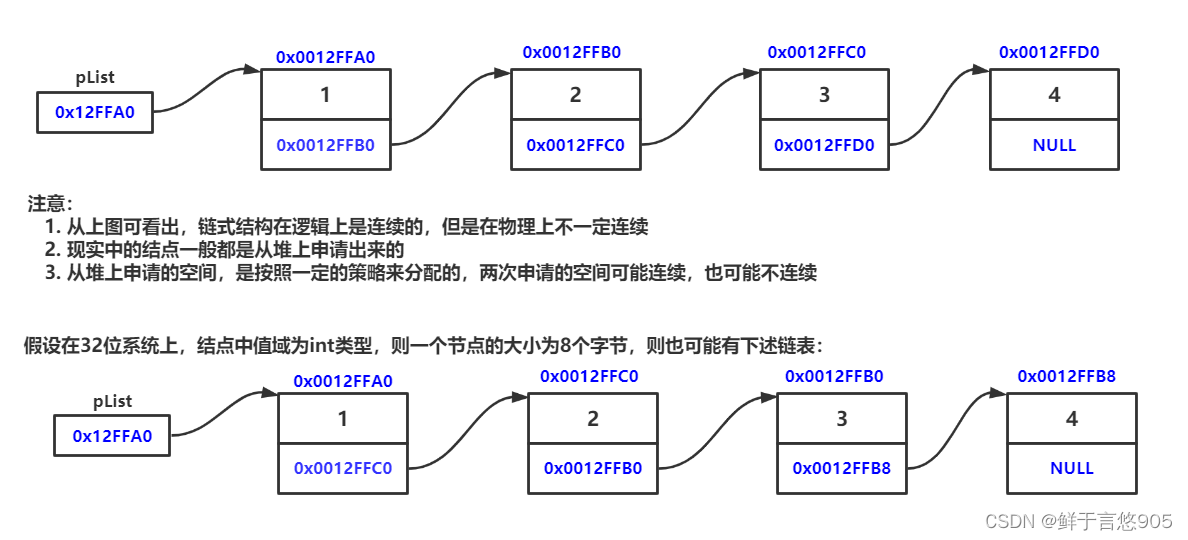
1.2 鏈表的分類
實際中鏈表的結構非常多樣,以下情況組合起來就有8種鏈表結構:
- 單向或者雙向
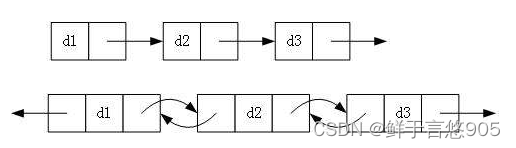
- 帶頭或者不帶頭
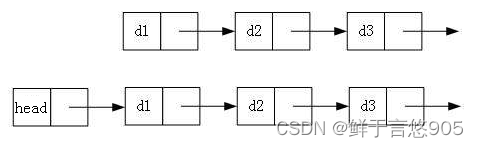
- 循環或者非循環
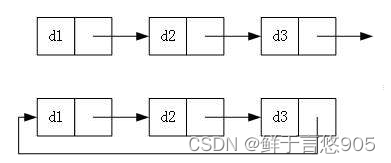
雖然有這么多的鏈表的結構,但是我們實際中最常用還是兩種結構:
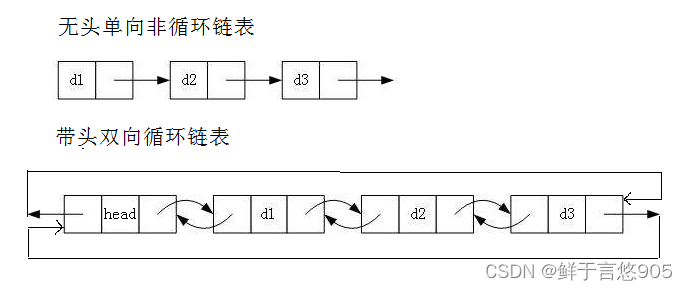
- 無頭單向非循環鏈表:結構簡單,一般不會單獨用來存數據。實際中更多是作為其他數據結
構的子結構,如哈希桶、圖的鄰接表等等。另外這種結構在筆試面試中出現很多。 - 帶頭雙向循環鏈表:結構最復雜,一般用在單獨存儲數據。實際中使用的鏈表數據結構,都
是帶頭雙向循環鏈表。另外這個結構雖然結構復雜,但是使用代碼實現以后會發現結構會帶
來很多優勢,實現反而簡單了,后面我們代碼實現了就知道了。
1.3 鏈表的實現
// 1、無頭+單向+非循環鏈表增刪查改實現
typedef int SLTDateType;
typedef struct SListNode
{SLTDateType data;struct SListNode* next;
}SListNode;
// 動態申請一個結點
SListNode* BuySListNode(SLTDateType x);
// 單鏈表打印
void SListPrint(SListNode* plist);
// 單鏈表尾插
void SListPushBack(SListNode** pplist, SLTDateType x);
// 單鏈表的頭插
void SListPushFront(SListNode** pplist, SLTDateType x);
// 單鏈表的尾刪
void SListPopBack(SListNode** pplist);
// 單鏈表頭刪
void SListPopFront(SListNode** pplist);
// 單鏈表查找
SListNode* SListFind(SListNode* plist, SLTDateType x);
// 單鏈表在pos位置之后插入x
// 分析思考為什么不在pos位置之前插入?
void SListInsertAfter(SListNode* pos, SLTDateType x);
// 單鏈表刪除pos位置之后的值
// 分析思考為什么不刪除pos位置?
void SListEraseAfter(SListNode* pos);
1.4 鏈表面試題
- 刪除鏈表中等于給定值 val 的所有結點
- 反轉一個單鏈表
- 給定一個帶有頭結點 head 的非空單鏈表,返回鏈表的中間結點。如果有兩個中間結點,則
返回第二個中間結點 - 輸入一個鏈表,輸出該鏈表中倒數第k個結點
- 將兩個有序鏈表合并為一個新的有序鏈表并返回。新鏈表是通過拼接給定的兩個鏈表的所有
結點組成的 - 編寫代碼,以給定值x為基準將鏈表分割成兩部分,所有小于x的結點排在大于或等于x的結
點之前 - 鏈表的回文結構
- 輸入兩個鏈表,找出它們的第一個公共結點
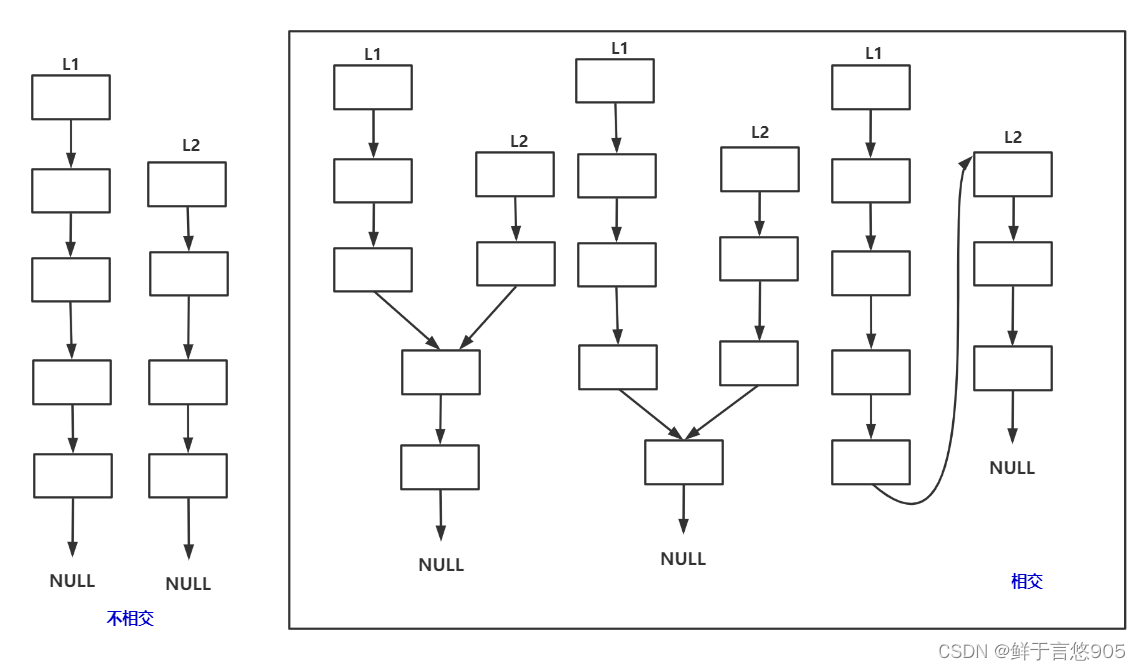
- 給定一個鏈表,判斷鏈表中是否有環
【思路】
快慢指針,即慢指針一次走一步,快指針一次走兩步,兩個指針從鏈表其實位置開始運行,如果鏈表帶環則一定會在環中相遇,否則快指針率先走到鏈表的末尾。比如:陪女朋友到操作跑步減肥。
【擴展問題】
-
為什么快指針每次走兩步,慢指針走一步可以?
假設鏈表帶環,兩個指針最后都會進入環,快指針先進環,慢指針后進環。當慢指針剛進環時,可能就和快指針相遇了,最差情況下兩個指針之間的距離剛好就是環的長度。
此時,兩個指針每移動一次,之間的距離就縮小一步,不會出現每次剛好是套圈的情況,因此:在滿指針走到一圈之前,快指針肯定是可以追上慢指針的,即相遇。 -
快指針一次走3步,走4步,…n步行嗎?

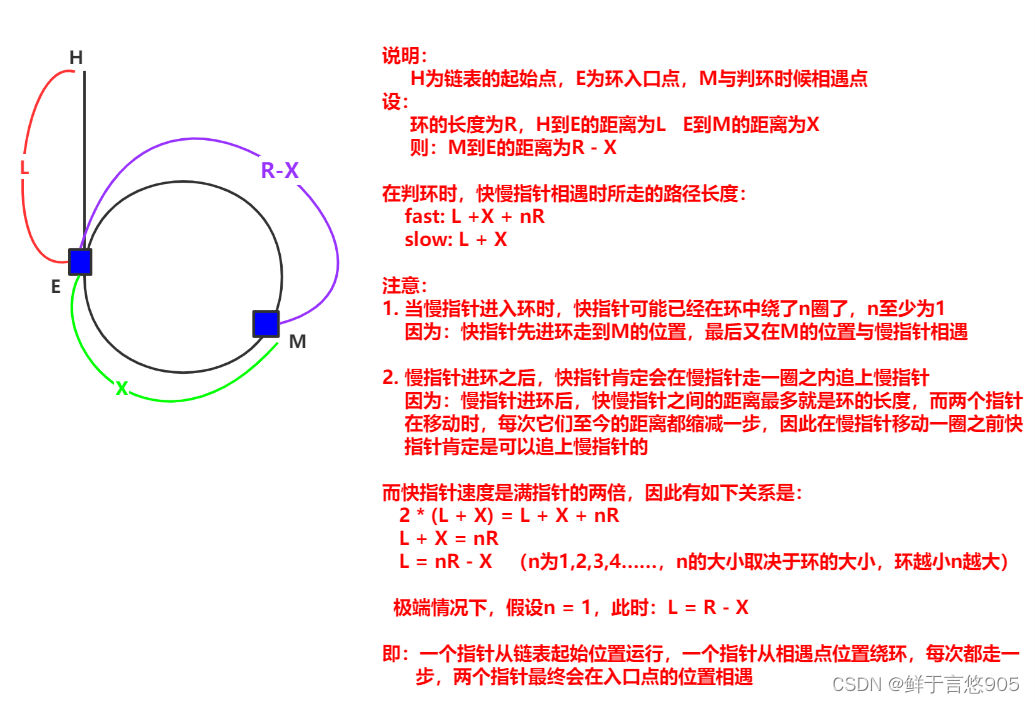
- 給定一個鏈表,返回鏈表開始入環的第一個結點。 如果鏈表無環,則返回 NULL
- 結論
讓一個指針從鏈表起始位置開始遍歷鏈表,同時讓一個指針從判環時相遇點的位置開始繞環
運行,兩個指針都是每次均走一步,最終肯定會在入口點的位置相遇。 - 證明
- 給定一個鏈表,每個結點包含一個額外增加的隨機指針,該指針可以指向鏈表中的任何結點
或空結點。
要求返回這個鏈表的深度拷貝 - 其他 。ps:鏈表的題當前因為難度及知識面等等原因還不適合我們當前學習,大家可以先把
c++學一下,在逐步開始刷題 Leetcode + 牛客
1.5 雙向鏈表的實現
// 2、帶頭+雙向+循環鏈表增刪查改實現
typedef int LTDataType;
typedef struct ListNode
{LTDataType _data;struct ListNode* next;struct ListNode* prev;
}ListNode;
// 創建返回鏈表的頭結點.
ListNode* ListCreate();
// 雙向鏈表銷毀
void ListDestory(ListNode* plist);
// 雙向鏈表打印
void ListPrint(ListNode* plist);
// 雙向鏈表尾插
void ListPushBack(ListNode* plist, LTDataType x);
// 雙向鏈表尾刪
void ListPopBack(ListNode* plist);
// 雙向鏈表頭插
void ListPushFront(ListNode* plist, LTDataType x);
// 雙向鏈表頭刪
void ListPopFront(ListNode* plist);
// 雙向鏈表查找
ListNode* ListFind(ListNode* plist, LTDataType x);
// 雙向鏈表在pos的前面進行插入
void ListInsert(ListNode* pos, LTDataType x);
// 雙向鏈表刪除pos位置的結點
void ListErase(ListNode* pos);
二、順序表和鏈表的區別
| 不同點 | 順序表 | 鏈表 |
|---|---|---|
| 存儲空間上 | 物理上一定連續 | 邏輯上連續,但物理上不一定連續 |
| 隨機訪問 | 支持O(1) | 不支持:O(N) |
| 任意位置插入或者刪除元素 | 可能需要搬移元素,效率低O(N) | 只需修改指針指向 |
| 插入 | 動態順序表,空間不夠時需要擴容 | 沒有容量的概念 |
| 應用場景 | 元素高效存儲+頻繁訪問 | 任意位置插入和刪除頻繁 |
| 緩存利用率 | 高 | 低 |
備注:緩存利用率參考存儲體系結構 以及 局部原理性。
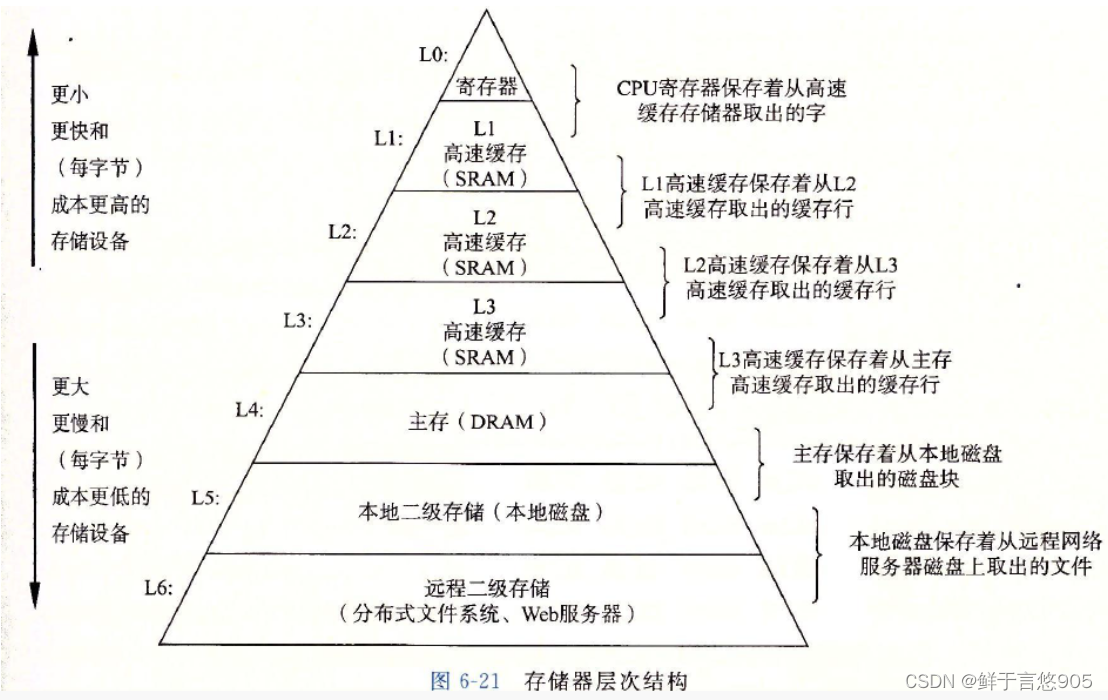
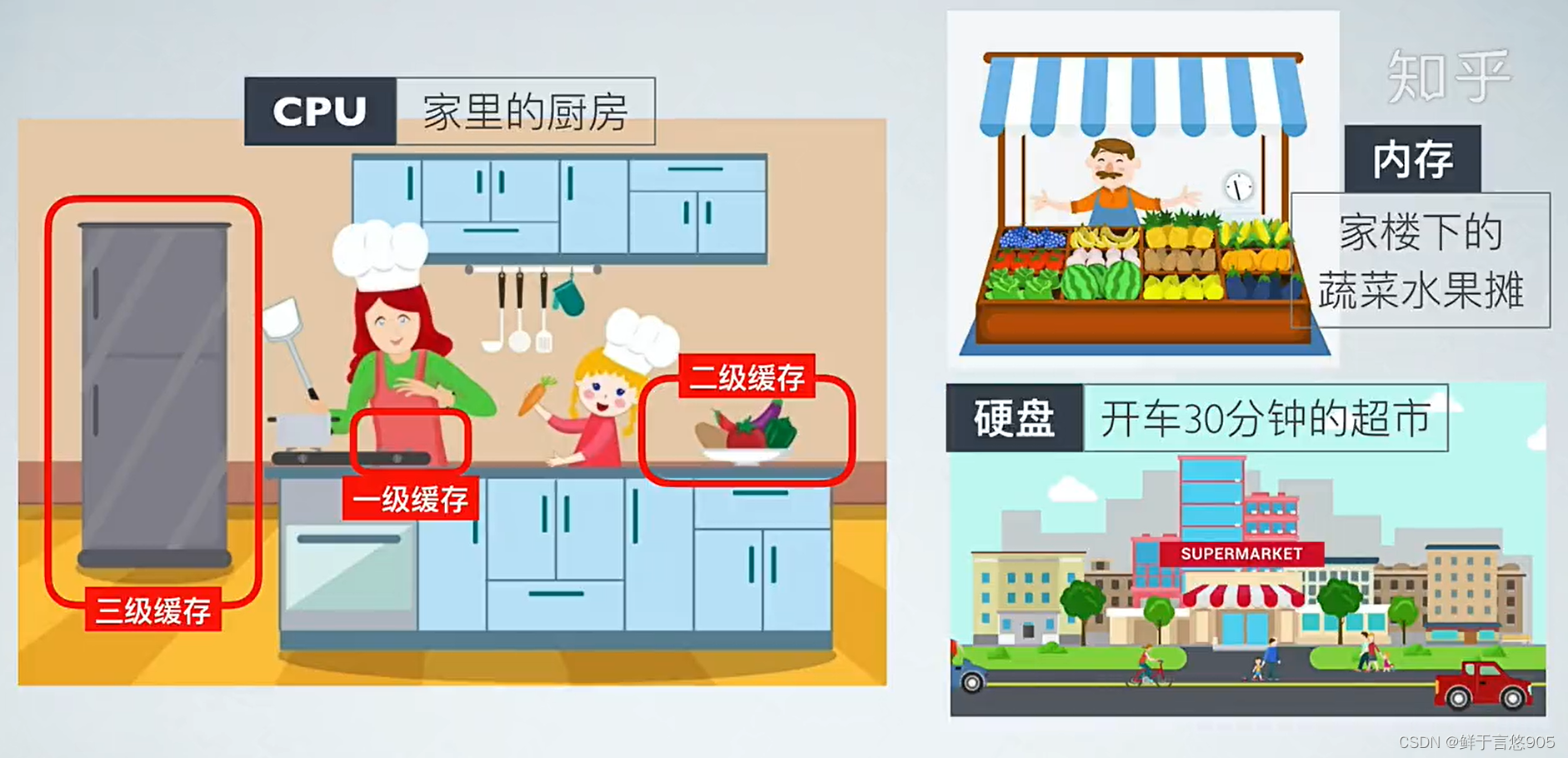
與程序員相關的CPU緩存知識
三、單項鏈表實現具體代碼
text.h
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>typedef int SLTDataType;typedef struct SListNode
{SLTDataType data;struct SListNode* next;
}SLTNode,*Node;void SLTPrint(Node phead);
Node SLTBuyNode(SLTDataType x);//開辟空間
//鏈表的頭插、尾插
void SLTPushBack(Node* pphead, SLTDataType x);
void SLTPushFront(Node* pphead, SLTDataType x);//鏈表的頭刪、尾刪
void SLTPopBack(Node* pphead);//尾刪
void SLTPopFront(Node* pphead);//頭刪//查找
Node SLTFind(Node* pphead, SLTDataType x);//在指定位置之前插入數據
void SLTInsert(Node* pphead, Node pos, SLTDataType x);
//在指定位置之后插入數據
void SLTInsertAfter(Node pos, SLTDataType x);//刪除pos節點
void SLTErase(Node* pphead, Node pos);
//刪除pos之后的節點
void SLTEraseAfter(Node pos);//銷毀鏈表
void SListDesTroy(Node* pphead);
text.c
#include "text.h"
void SLTPrint(Node phead)
{assert(phead);Node purt = phead;while (purt){printf("%d->", purt->data);purt = purt->next;}printf("NULL\n");
}
Node SLTBuyNode(SLTDataType x)
{Node str = (Node)malloc(sizeof(SLTNode));assert(str);str->data = x;str->next = NULL;return str;
}
void SLTPushBack(Node* pphead, SLTDataType x)
{assert(pphead);Node newnode = SLTBuyNode(x);if (*pphead == NULL){*pphead = newnode;}else{Node ptail = *pphead;while (ptail->next){ptail = ptail->next;}ptail->next = newnode;}
}
void SLTPushFront(Node* pphead, SLTDataType x)
{assert(pphead);Node newnode = SLTBuyNode(x);newnode->next = *pphead;*pphead = newnode;
}
void SLTPopBack(Node* pphead)
{assert(pphead);assert(*pphead);if ((*pphead)->next == NULL){free(*pphead);*pphead = NULL;}Node ptail = *pphead;while (ptail->next->next){ptail = ptail->next;}free(ptail->next);ptail->next= NULL;
}
void SLTPopFront(Node* pphead)
{assert(pphead);assert(*pphead);Node next = (*pphead)->next;free(*pphead);(*pphead) = next;
}
Node SLTFind(Node* pphead, SLTDataType x)
{assert(pphead);assert(*pphead);Node next = *pphead;while (next){if (next->data == x){printf("找到了\n");return next;}next = next->next;}return NULL;
}
void SLTInsert(Node* pphead, Node pos, SLTDataType x) {assert(pphead);assert(pos);//要加上鏈表不能為空assert(*pphead);Node newnode = SLTBuyNode(x);//pos剛好是頭結點if (pos == *pphead) {//頭插SLTPushFront(pphead, x);return;}//pos不是頭結點的情況Node prev = *pphead;while (prev->next != pos){prev = prev->next;}//prev -> newnode -> posprev->next = newnode;newnode->next = pos;
}
void SLTInsertAfter(Node pos, SLTDataType x)
{assert(pos);Node newnode = SLTBuyNode(x);newnode->next = pos->next;pos->next = newnode;
}
void SLTErase(Node* pphead, Node pos)
{assert(pphead);assert(*pphead);assert(pos);Node node = *pphead;if (pos == *pphead){SLTPopFront(&pos);}while (node->next != pos){node = node->next;}node->next = pos->next;free(pos);pos = NULL;
}
void SLTEraseAfter(Node pos)
{assert(pos);assert(pos->next);Node next = pos->next,pre;while (next){pre = next->next;free(next);next = pre;}pos->next = NULL;
}
void SListDesTroy(Node* pphead) {assert(pphead);assert(*pphead);Node pcur = *pphead;while (pcur){Node next = pcur->next;free(pcur);pcur = next;}*pphead = NULL;
}
main.c
#include"text.h"void SlistTest01() {//一般不會這樣去創建鏈表,這里只是為了給大家展示鏈表的打印SLTNode* node1 = (SLTNode*)malloc(sizeof(SLTNode));node1->data = 1;SLTNode* node2 = (SLTNode*)malloc(sizeof(SLTNode));node2->data = 2;SLTNode* node3 = (SLTNode*)malloc(sizeof(SLTNode));node3->data = 3;SLTNode* node4 = (SLTNode*)malloc(sizeof(SLTNode));node4->data = 4;node1->next = node2;node2->next = node3;node3->next = node4;node4->next = NULL;SLTNode* plist = node1;SLTPrint(plist);
}
void SlistTest02() {Node plist = NULL;SLTPushBack(&plist, 1);SLTPushBack(&plist, 2);SLTPushBack(&plist, 3);SLTPushBack(&plist, 4);SLTPrint(plist); //1->2->3->4->NULLSLTPushFront(&plist, 5);SLTPrint(plist); //5->1->2->3->4->NULLSLTPushFront(&plist, 6);SLTPrint(plist); //6->5->1->2->3->4->NULLSLTPushFront(&plist, 7);SLTPrint(plist); //7-6->5->1->2->3->4->NULLSLTPopBack(&plist);SLTPrint(plist);//1->2->3->NULLSLTPopBack(&plist);SLTPrint(plist);//1->2->3->NULLSLTPopBack(&plist);SLTPrint(plist);//1->2->3->NULLSLTPopBack(&plist);SLTPrint(plist);//1->2->3->NULLSLTPopBack(&plist);SLTPrint(plist);//1->2->3->NULL
}void SlistTest03() {Node plist = NULL;SLTPushBack(&plist, 1);SLTPushBack(&plist, 2);SLTPushBack(&plist, 3);SLTPushBack(&plist, 4);SLTPrint(plist); //1->2->3->4->NULL/*SListDesTroy(&plist);*///頭刪SLTPopFront(&plist);SLTPrint(plist); //2->3->4->NULLSLTPopFront(&plist);SLTPrint(plist); //3->4->NULLSLTPopFront(&plist);SLTPrint(plist); //4->NULL//SLTPopFront(&plist);//SLTPrint(plist); //NULLSLTPopFront(&plist);SLTPrint(plist); //assertSLTNode* FindRet = SLTFind(&plist, 3);if (FindRet) {printf("找到了!\n");}else {printf("未找到!\n");}//SLTInsert(&plist, FindRet, 100);//SLTInsertAfter(FindRet, 100);//刪除指定位置的節點//SLTErase(&plist, FindRet);//SLTPrint(plist); //1->2->3->NULL
}
int main() {//SlistTest01();/*SlistTest02();*/SlistTest03();return 0;
}
單鏈表的打印
void SLTPrint(Node phead)
void SLTPrint(Node phead)
{assert(phead);Node purt = phead;while (purt){printf("%d->", purt->data);purt = purt->next;}printf("NULL\n");
}
單鏈表的打印是鏈表操作中的一個基礎且重要的環節。鏈表是一種常見的數據結構,它由一系列節點組成,每個節點包含數據部分和指向下一個節點的指針。而單鏈表則是鏈表的一種,它的特點是每個節點只包含一個指向下一個節點的指針。
在打印單鏈表時,我們通常需要遍歷整個鏈表,依次訪問每個節點,并輸出節點的數據部分。這個過程可以通過設置一個指針,初始時指向鏈表的頭節點,然后不斷將指針移動到下一個節點,直到指針為空,即遍歷完整個鏈表。
為了實現單鏈表的打印,我們可以定義一個函數,該函數接受鏈表的頭節點作為參數。在函數內部,我們使用一個循環來遍歷鏈表。在每次循環中,我們輸出當前節點的數據部分,并將指針移動到下一個節點。當指針為空時,循環結束,打印操作完成。
空間的開辟
Node SLTBuyNode(SLTDataType x);//開辟空間
Node SLTBuyNode(SLTDataType x)
{Node str = (Node)malloc(sizeof(SLTNode));assert(str);str->data = x;str->next = NULL;return str;
}
鏈表的頭插、尾插
//鏈表的頭插、尾插
void SLTPushBack(Node* pphead, SLTDataType x);
void SLTPushFront(Node* pphead, SLTDataType x);
void SLTPushBack(Node* pphead, SLTDataType x)
{assert(pphead);Node newnode = SLTBuyNode(x);if (*pphead == NULL){*pphead = newnode;}else{Node ptail = *pphead;while (ptail->next){ptail = ptail->next;}ptail->next = newnode;}
}
void SLTPushFront(Node* pphead, SLTDataType x)
{assert(pphead);Node newnode = SLTBuyNode(x);newnode->next = *pphead;*pphead = newnode;
}
鏈表的頭插、尾插是鏈表操作中常見的兩種插入方式,它們在處理鏈表數據結構時各有特點,也適用于不同的應用場景。
頭插法,顧名思義,是在鏈表的頭部插入新的節點。這種操作的時間復雜度通常為O(1),因為無論鏈表長度如何,只需要修改頭指針和新節點的指針即可。頭插法的優點是插入速度快,但缺點是在某些情況下可能導致鏈表變得不均衡,特別是在大量連續的頭插操作中,鏈表可能會退化成類似棧的結構,影響后續操作的效率。
尾插法則是在鏈表的尾部插入新的節點。這種操作的時間復雜度通常為O(n),因為需要遍歷鏈表找到尾節點。尾插法的優點是能保持鏈表的相對均衡,減少鏈表操作中的性能瓶頸。然而,它的缺點是在大量連續的尾插操作中,需要不斷遍歷鏈表,相對頭插法來說效率較低。
在實際應用中,選擇頭插還是尾插,需要根據具體的需求和場景來決定。例如,在實現一個基于鏈表的棧時,頭插法是一個很好的選擇,因為棧的特性就是后進先出(LIFO),頭插法能很好地滿足這一需求。而在實現一個基于鏈表的隊列時,尾插法則更為合適,因為隊列的特性是先進先出(FIFO),尾插法能保持鏈表的順序性,使得出隊操作更加高效。
此外,在實際編程中,還需要注意鏈表操作的邊界條件和特殊情況,如空鏈表的處理、內存分配失敗的處理等。
鏈表的頭刪、尾刪
//鏈表的頭刪、尾刪
void SLTPopBack(Node* pphead);//尾刪
void SLTPopFront(Node* pphead);//頭刪
void SLTPopBack(Node* pphead)
{assert(pphead);assert(*pphead);if ((*pphead)->next == NULL){free(*pphead);*pphead = NULL;}Node ptail = *pphead;while (ptail->next->next){ptail = ptail->next;}free(ptail->next);ptail->next= NULL;
}
void SLTPopFront(Node* pphead)
{assert(pphead);assert(*pphead);Node next = (*pphead)->next;free(*pphead);(*pphead) = next;
}
鏈表的頭刪、尾刪是鏈表操作中的基礎內容,對于理解鏈表結構和實現鏈表功能至關重要。在鏈表中,頭刪指的是刪除鏈表中的第一個元素,而尾刪則是刪除鏈表中的最后一個元素。這個過程中,需要注意更新頭節點的指針,并確保原頭節點在刪除后能夠被正確釋放,以避免內存泄漏。
相比之下,尾刪操作稍微復雜一些。因為需要找到鏈表的最后一個節點,并將其前一個節點的指針設置為null。同樣,在刪除尾節點之前,也需要判斷鏈表是否為空。如果鏈表只有一個節點,那么頭刪和尾刪是等價的。如果鏈表有多個節點,則需要遍歷鏈表,找到最后一個節點,并執行刪除操作。
除了基本的頭刪和尾刪操作,鏈表還支持在中間位置插入和刪除節點。這些操作同樣需要對鏈表結構有深入的理解,并且能夠正確處理各種邊界情況。在實際應用中,鏈表的操作通常與其他數據結構或算法相結合,以實現更復雜的功能。通過熟練掌握鏈表操作,可以更好地理解和應用鏈表這一基礎數據結構。
鏈表中元素的查找
//查找
Node SLTFind(Node* pphead, SLTDataType x);
Node SLTFind(Node* pphead, SLTDataType x)
{assert(pphead);assert(*pphead);Node next = *pphead;while (next){if (next->data == x){printf("找到了\n");return next;}next = next->next;}return NULL;
}
鏈表中元素的查找是數據結構和算法中的一個基礎問題。在鏈表中查找元素,不同于在數組中的直接索引訪問,它通常需要從鏈表的頭部或尾部開始,逐個節點地遍歷,直到找到目標元素或者遍歷完整個鏈表。這種查找方式的時間復雜度通常是O(n),其中n是鏈表的長度。
鏈表的查找性能可以通過一些優化手段來提升。例如,如果鏈表是有序的,那么可以使用二分查找等更高效的算法來減少查找時間。然而,這種優化通常要求鏈表在插入和刪除元素時保持有序狀態,這會增加這些操作的復雜度。
在實現鏈表查找時,我們通常會使用一個循環來遍歷鏈表。在每次迭代中,我們將當前節點的值與目標值進行比較。如果找到匹配的值,則返回當前節點的位置或引用;如果遍歷完整個鏈表都沒有找到匹配的值,則返回null或表示未找到的特殊值。
鏈表在指定位置之前、之后插入數據
//在指定位置之前插入數據
void SLTInsert(Node* pphead, Node pos, SLTDataType x);
//在指定位置之后插入數據
void SLTInsertAfter(Node pos, SLTDataType x);
void SLTInsert(Node* pphead, Node pos, SLTDataType x) {assert(pphead);assert(pos);//要加上鏈表不能為空assert(*pphead);Node newnode = SLTBuyNode(x);//pos剛好是頭結點if (pos == *pphead) {//頭插SLTPushFront(pphead, x);return;}//pos不是頭結點的情況Node prev = *pphead;while (prev->next != pos){prev = prev->next;}//prev -> newnode -> posprev->next = newnode;newnode->next = pos;
}
void SLTInsertAfter(Node pos, SLTDataType x)
{assert(pos);Node newnode = SLTBuyNode(x);newnode->next = pos->next;pos->next = newnode;
}
鏈表在指定位置之前、之后插入數據是鏈表操作中的基本功能。鏈表作為一種常見的數據結構,由一系列節點組成,每個節點包含數據和指向下一個節點的指針。這種結構允許我們在不移動其他元素的情況下插入或刪除元素,因此在許多場景中都非常有用。
首先,我們要明確鏈表的基本結構。通常,鏈表節點包含一個數據域和一個指針域。數據域用于存儲實際的數據,而指針域則用于指向鏈表中的下一個節點。對于頭節點,其指針域指向鏈表的第一個節點;對于尾節點,其指針域通常指向空(NULL),表示鏈表的結束。
在鏈表中插入數據之前,我們需要確定插入的位置。這可以通過使用索引或遍歷鏈表直到找到適當的節點來實現。一旦找到插入位置,我們就可以創建一個新的節點,并將其插入到鏈表中。
要在指定位置之后插入數據,我們需要找到該位置的前一個節點。然后,我們將新節點的指針域設置為當前節點的指針域所指向的節點,同時將當前節點的指針域設置為新節點。這樣,新節點就被插入到了指定位置之后。
要在指定位置之前插入數據,我們需要找到該位置的節點。然后,我們將新節點的指針域設置為當前節點,并將當前節點的前一個節點的指針域設置為新節點。這樣,新節點就被插入到了指定位置之前。
需要注意的是,在插入節點時,我們必須確保正確地更新指針域,以保持鏈表的完整性和正確性。此外,我們還需要考慮鏈表的邊界情況,例如在鏈表頭部或尾部插入節點時。
在插入數據后,鏈表的結構可能會發生變化,因此任何依賴于鏈表結構的操作都可能需要重新評估或調整。此外,插入操作可能會增加鏈表的長度,這可能會影響鏈表的性能,特別是在進行搜索或遍歷操作時。
總的來說,鏈表在指定位置之前或之后插入數據是鏈表操作中的基本操作之一。通過正確地實現這些操作,我們可以充分利用鏈表的優勢,高效地管理和操作數據。
刪除鏈表中的結點
//刪除pos節點
void SLTErase(Node* pphead, Node pos);
//刪除pos之后的節點
void SLTEraseAfter(Node pos);
void SLTErase(Node* pphead, Node pos)
{assert(pphead);assert(*pphead);assert(pos);Node node = *pphead;if (pos == *pphead){SLTPopFront(&pos);}while (node->next != pos){node = node->next;}node->next = pos->next;free(pos);pos = NULL;
}
void SLTEraseAfter(Node pos)
{assert(pos);assert(pos->next);Node next = pos->next,pre;while (next){pre = next->next;free(next);next = pre;}pos->next = NULL;
}
刪除鏈表中的結點是一項常見的編程任務,它要求我們在保持鏈表其他部分完整的同時,移除指定的結點。鏈表是一種常見的數據結構,它由一系列節點組成,每個節點都包含數據部分和指向下一個節點的指針。為了有效地刪除鏈表中的某個節點,我們需要遵循一定的步驟,并確保不會破壞鏈表的完整性。
首先,我們需要確定要刪除的節點。這通常是通過節點的值或者節點在鏈表中的位置來實現的。在知道要刪除的節點之后,我們需要考慮幾種不同的刪除情況:
如果要刪除的節點是鏈表的第一個節點,我們需要更新鏈表的頭指針,使其指向第二個節點。
如果要刪除的節點是鏈表的最后一個節點,我們需要找到倒數第二個節點,并將其指針部分設置為null,從而切斷與最后一個節點的連接。
如果要刪除的節點位于鏈表的中間,我們需要找到該節點的前一個節點,并將其指針部分更新為指向要刪除節點的下一個節點,從而跳過要刪除的節點。
在刪除節點的過程中,我們必須確保正確地處理內存,以防止內存泄漏。這通常意味著在刪除節點后,我們需要釋放該節點所占用的內存。
銷毀鏈表
//銷毀鏈表
void SListDesTroy(Node* pphead);
void SListDesTroy(Node* pphead) {assert(pphead);assert(*pphead);Node pcur = *pphead;while (pcur){Node next = pcur->next;free(pcur);pcur = next;}*pphead = NULL;
}
鏈表,這種數據結構在計算機科學中占據著舉足輕重的地位,其通過節點之間的鏈接來存儲數據,每個節點都包含數據和指向下一個節點的指針。然而,當鏈表不再需要時,如何正確地銷毀它,釋放其占用的內存,就顯得尤為重要。
銷毀鏈表的過程通常包括兩個主要步驟:遍歷鏈表和釋放內存。首先,我們需要從鏈表的頭節點開始,逐個訪問鏈表中的每個節點。在訪問每個節點時,我們需要記錄下一個節點的位置,以便在釋放當前節點后能夠繼續遍歷鏈表。同時,我們還需要注意處理鏈表的尾節點,確保不會出現內存泄漏。
在遍歷鏈表的過程中,我們可以通過修改指針的指向來逐個斷開節點之間的鏈接。具體來說,我們可以將當前節點的下一個節點的指針置為null,這樣當前節點就不再指向下一個節點,從而實現了斷開鏈接的目的。然后,我們可以釋放當前節點所占用的內存,通常可以使用操作系統提供的內存釋放函數來完成這一操作。
在釋放內存時,我們需要格外小心。一方面,我們需要確保只釋放鏈表節點所占用的內存,而不要誤釋放其他重要數據的內存。另一方面,我們還需要注意處理可能出現的異常情況,例如內存釋放失敗等。為了避免這些問題,我們可以使用智能指針等高級內存管理技術來輔助銷毀鏈表。
總的來說,銷毀鏈表是一個復雜而重要的任務。我們需要仔細遍歷鏈表中的每個節點,逐個斷開鏈接并釋放內存,以確保鏈表能夠被正確地銷毀。同時,我們還需要注意處理可能出現的異常情況,保證程序的穩定性和可靠性。只有這樣,我們才能在享受鏈表帶來的便利的同時,避免其帶來的潛在風險。
四、雙向循環鏈表代碼的具體實現
text.h
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include<assert.h>//定義雙向鏈表中節點的結構
typedef int LTDataType;
typedef struct ListNode {LTDataType data;struct ListNode* prev;struct ListNode* next;
}LTNode,* Node;//注意,雙向鏈表是帶有哨兵位的,插入數據之前鏈表中必須要先初始化一個哨兵位
//void LTInit(Node* pphead);
Node LTInit();
Node LTBuyNode(LTDataType x);
//void LTDesTroy(Node* pphead);
void LTDesTroy(Node phead); //推薦一級(保持接口一致性)void LTPrint(Node phead);//不需要改變哨兵位,則不需要傳二級指針
//如果需要修改哨兵位的話,則傳二級指針
void LTPushBack(Node phead, LTDataType x);
void LTPushFront(Node phead, LTDataType x);//頭刪、尾刪
void LTPopBack(Node phead);
void LTPopFront(Node phead);//查找
Node LTFind(Node phead, LTDataType x);//在pos位置之后插入數據
void LTInsert(Node pos, LTDataType x);
//刪除pos位置的數據
void LTErase(Node pos);
text.c
#include "text.h"
Node LTBuyNode(LTDataType x)
{Node phead = (Node)malloc(sizeof(LTNode));assert(phead);phead->data = x;phead->prev = phead;phead->next = phead;return phead;
}
Node LTInit()
{Node phead = LTBuyNode(-1);return phead;
}
void LTDesTroy(Node phead)
{assert(phead);/*Node ret;while (phead->next != phead){ret = phead->next;phead->next = ret->next;phead->next->prev = phead;free(ret);}free(phead);phead = NULL;*/Node pur = phead->next;while (pur != phead){Node next = pur->next;free(pur);pur = next;}free(phead);phead = NULL;
}
void LTPrint(Node phead)
{assert(phead);Node pur = phead->next;while (pur!= phead){printf("%d->", pur->data);pur = pur->next;}printf("NULL\n");
}
void LTPushBack(Node phead, LTDataType x)
{assert(phead);Node newnode = LTBuyNode(x);phead->prev->next = newnode;newnode->prev = phead->prev;newnode->next = phead;phead->prev = newnode;
}
void LTPushFront(Node phead, LTDataType x)
{assert(phead);Node newnode = LTBuyNode(x);newnode->next = phead->next;phead->next->prev = newnode;newnode->prev = phead;phead->next = newnode;
}
void LTPopBack(Node phead)
{assert(phead);assert(phead->next != phead);Node pur = phead->prev;pur->prev->next = phead;phead->prev = pur->prev;free(pur);pur = NULL;
}
void LTPopFront(Node phead)
{assert(phead);assert(phead->next != phead);Node pur = phead->next;phead->next = pur->next;pur->next->prev = phead;free(pur);pur = NULL;
}Node LTFind(Node phead, LTDataType x)
{assert(phead);Node pur = phead->next;while (pur != phead){if (pur->data == x)return pur;pur = pur->next;}return NULL;
}
void LTInsert(Node pos, LTDataType x) {assert(pos);Node newnode = LTBuyNode(x);//pos newnode pos->nextnewnode->next = pos->next;newnode->prev = pos;pos->next->prev = newnode;pos->next = newnode;
}
//刪除pos位置的數據
void LTErase(Node pos) {assert(pos);//pos->prev pos pos->nextpos->next->prev = pos->prev;pos->prev->next = pos->next;free(pos);pos = NULL;
}
main.c
#include "text.h"
void ListTest01() {//LTNode* plist = NULL;//LTInit(&plist);Node plist = LTInit();//尾插/*LTPushBack(plist, 1);LTPushBack(plist, 2);LTPushBack(plist, 3);LTPushBack(plist, 4);LTPrint(plist);*///頭插LTPushFront(plist, 1);LTPushFront(plist, 2);LTPushFront(plist, 3);LTPushFront(plist, 4);LTPrint(plist); //4->3->2->1->///*LTPopBack(plist);LTPrint(plist);LTPopBack(plist);LTPrint(plist);LTPopBack(plist);LTPrint(plist);LTPopBack(plist);LTPrint(plist);LTPopBack(plist);*///LTPrint(plist);////頭刪/*LTPopFront(plist);LTPrint(plist);LTPopFront(plist);LTPrint(plist);LTPopFront(plist);LTPrint(plist);LTPopFront(plist);LTPrint(plist);LTPopFront(plist);*///LTPrint(plist);Node findRet = LTFind(plist, 3);if (findRet == NULL) {printf("未找到!\n");}else {printf("找到了!\n");}在指定位置之后插入數據LTInsert(findRet, 66); //4->3->2->1->66->LTPrint(plist);//刪除pos位置的節點LTErase(findRet);LTPrint(plist);LTDesTroy(plist);plist = NULL;
}int main() {ListTest01();return 0;
}
雙向循環鏈表的創建
Node LTBuyNode(LTDataType x);
Node LTBuyNode(LTDataType x)
{Node phead = (Node)malloc(sizeof(LTNode));assert(phead);phead->data = x;phead->prev = phead;phead->next = phead;return phead;
}
雙向循環鏈表的初始化
Node LTInit();
Node LTInit()
{Node phead = LTBuyNode(-1);return phead;
}
在開始編寫雙向循環鏈表的初始化代碼之前,我們首先需要理解雙向循環鏈表的基本結構。雙向循環鏈表是一種線性數據結構,它包含了一個指向前一個節點的“前指針”和一個指向下一個節點的“后指針”。與傳統的雙向鏈表不同,雙向循環鏈表的最后一個節點的后指針指向第一個節點,而第一個節點的前指針則指向最后一個節點,從而形成一個閉環。
雙向循環鏈表的銷毀
void LTDesTroy(Node phead); //推薦一級(保持接口一致性)
void LTDesTroy(Node phead)
{assert(phead);/*Node ret;while (phead->next != phead){ret = phead->next;phead->next = ret->next;phead->next->prev = phead;free(ret);}free(phead);phead = NULL;*/Node pur = phead->next;while (pur != phead){Node next = pur->next;free(pur);pur = next;}free(phead);phead = NULL;
}
接口一致性
可以這樣理解,就想象你現在是用戶,你是想在使用這個軟件的時候操作簡單還是操作困難,按照正常人來說,肯定是越簡單越好,這時候就需要接口一致了,我們作為這個軟件的設計者,我們需要把這個軟件做的越簡單越好
在數據結構和算法的世界里,雙向循環鏈表是一種獨特而高效的數據結構。它允許我們在任意節點向前或向后移動,從而方便地訪問鏈表中的任何元素。然而,就像所有資源一樣,當我們不再需要雙向循環鏈表時,必須妥善地銷毀它,以防止內存泄漏和其他潛在問題。
銷毀雙向循環鏈表的過程涉及幾個關鍵步驟。首先,我們必須遍歷鏈表,釋放每個節點所占用的內存。由于雙向循環鏈表的特性,我們可以從任何一個節點開始遍歷。為了簡化操作,我們通常選擇頭節點作為起點。
在遍歷過程中,我們需要逐個訪問鏈表中的每個節點,并釋放其內存。這通常通過調用適當的內存釋放函數來完成,例如在C++中使用delete操作符,或在C語言中使用free函數。在釋放節點內存之前,我們還需確保已經斷開了該節點與前一個節點和后一個節點的連接,以防止出現懸掛指針。
一旦所有節點的內存都被釋放,我們就需要檢查鏈表的頭指針是否已經被正確設置為null或nullptr。這是為了確保鏈表已經被完全銷毀,并且任何嘗試訪問它的操作都會失敗。
值得注意的是,雙向循環鏈表的銷毀過程必須小心謹慎,以確保沒有遺漏任何節點。否則,未被釋放的內存可能會導致內存泄漏,進而影響程序的性能和穩定性。
綜上所述,雙向循環鏈表的銷毀是一個重要而必要的操作。通過正確地釋放每個節點的內存,并斷開它們之間的連接,我們可以確保鏈表被完全銷毀,從而避免潛在的內存泄漏和其他問題。這種負責任的資源管理實踐是編寫高效、可靠的代碼的重要組成部分。
雙向循環鏈表的打印
void LTPrint(Node phead);
void LTPrint(Node phead)
{assert(phead);Node pur = phead->next;while (pur!= phead){printf("%d->", pur->data);pur = pur->next;}printf("NULL\n");
}
雙向循環鏈表的頭插和尾插
//不需要改變哨兵位,則不需要傳二級指針
//如果需要修改哨兵位的話,則傳二級指針
void LTPushBack(Node phead, LTDataType x);
void LTPushFront(Node phead, LTDataType x);
void LTPushBack(Node phead, LTDataType x)
{assert(phead);Node newnode = LTBuyNode(x);phead->prev->next = newnode;newnode->prev = phead->prev;newnode->next = phead;phead->prev = newnode;
}
void LTPushFront(Node phead, LTDataType x)
{assert(phead);Node newnode = LTBuyNode(x);newnode->next = phead->next;phead->next->prev = newnode;newnode->prev = phead;phead->next = newnode;
}
雙向循環鏈表的頭刪和尾刪
//頭刪、尾刪
void LTPopBack(Node phead);
void LTPopFront(Node phead);
void LTPopBack(Node phead)
{assert(phead);assert(phead->next != phead);Node pur = phead->prev;pur->prev->next = phead;phead->prev = pur->prev;free(pur);pur = NULL;
}
void LTPopFront(Node phead)
{assert(phead);assert(phead->next != phead);Node pur = phead->next;phead->next = pur->next;pur->next->prev = phead;free(pur);pur = NULL;
}
雙向循環鏈表的元素查找
//查找
Node LTFind(Node phead, LTDataType x);
Node LTFind(Node phead, LTDataType x)
{assert(phead);Node pur = phead->next;while (pur != phead){if (pur->data == x)return pur;pur = pur->next;}return NULL;
}
雙向循環鏈表的插入和刪除
//在pos位置之后插入數據
void LTInsert(Node pos, LTDataType x);
//刪除pos位置的數據
void LTErase(Node pos);
void LTInsert(Node pos, LTDataType x) {assert(pos);Node newnode = LTBuyNode(x);//pos newnode pos->nextnewnode->next = pos->next;newnode->prev = pos;pos->next->prev = newnode;pos->next = newnode;
}
//刪除pos位置的數據
void LTErase(Node pos) {assert(pos);//pos->prev pos pos->nextpos->next->prev = pos->prev;pos->prev->next = pos->next;free(pos);pos = NULL;
}





)








函數的基本使用)
)



