一、定義

偶函數：定義域關于原點對稱，圖像關于Y軸對稱
f(x)=f(-x)
奇函數：定義域關于原點對稱，圖像關于原點中心對稱
f(x)+f(-x)=0 等價于 f(-x)=-f(x)

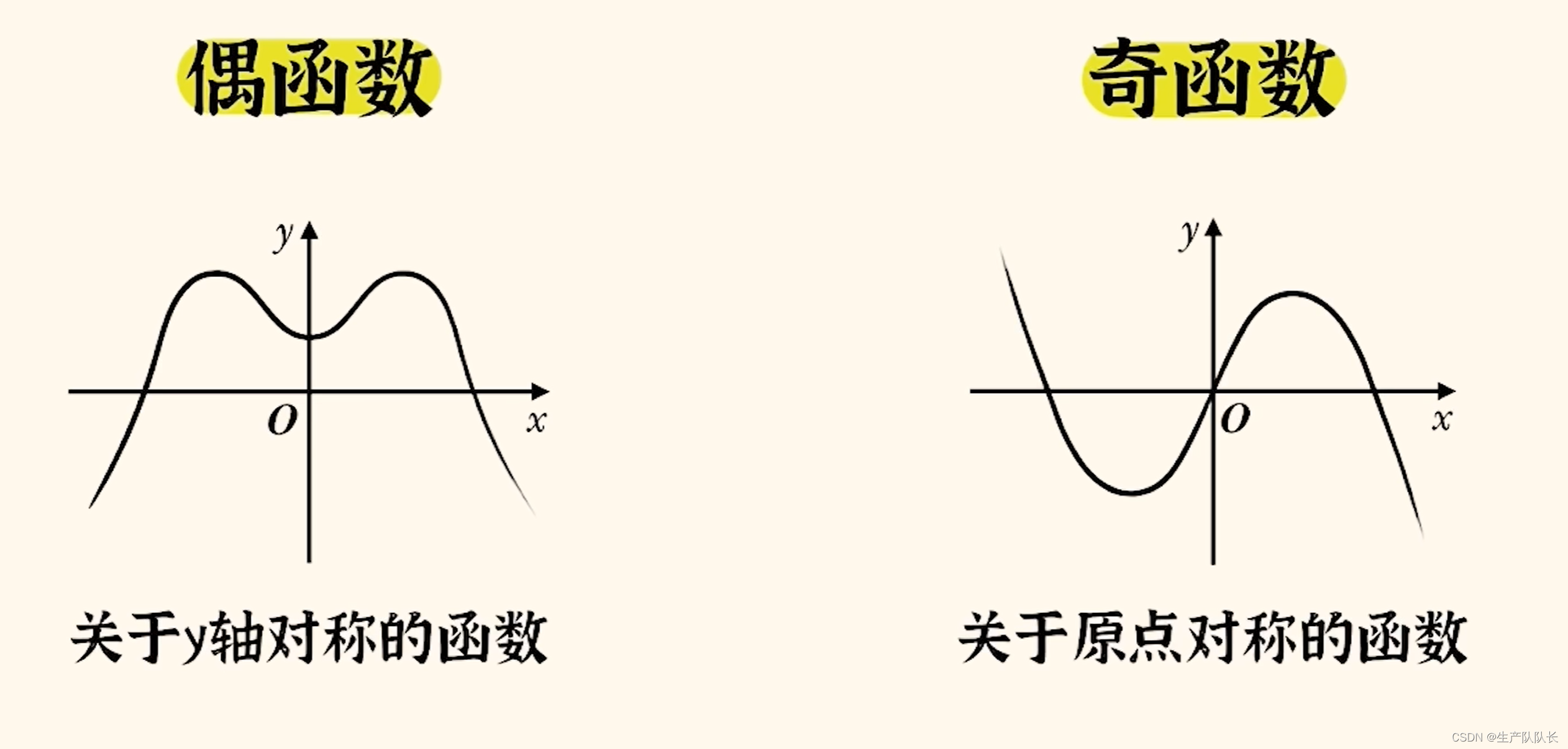
二、函數奇偶性的四種情況

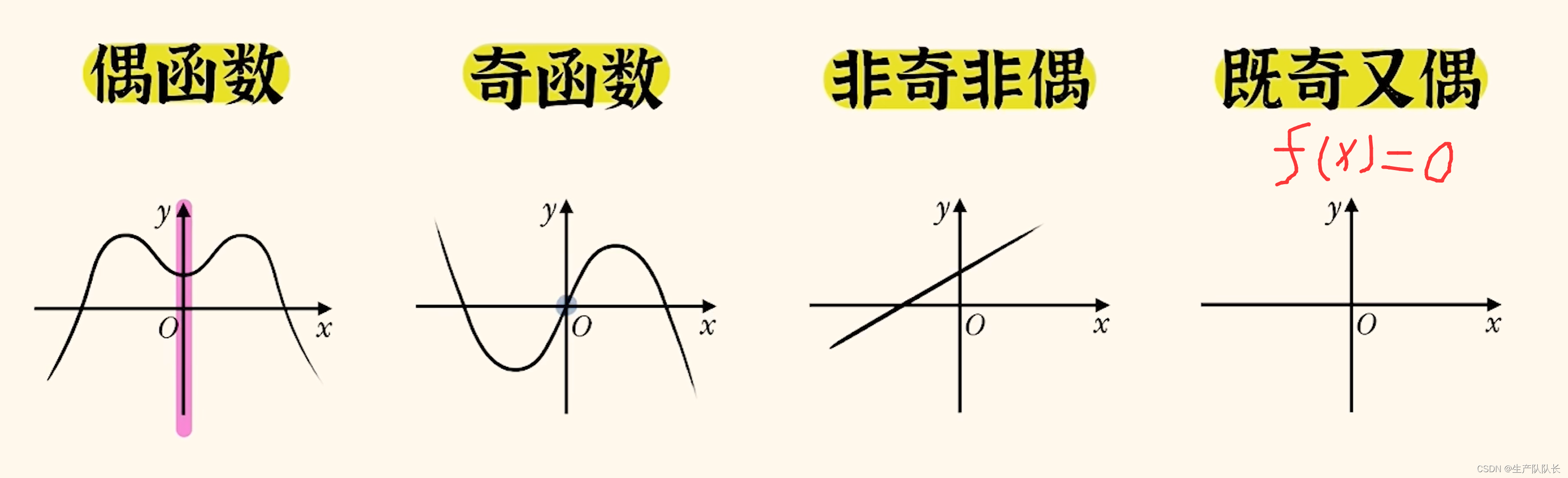
注意：
即奇又偶的函數，只有f(x)=0

三、常見奇偶函數

后面學習了對數函數，指數函數等函數，會補充此部分。

四、一般結論

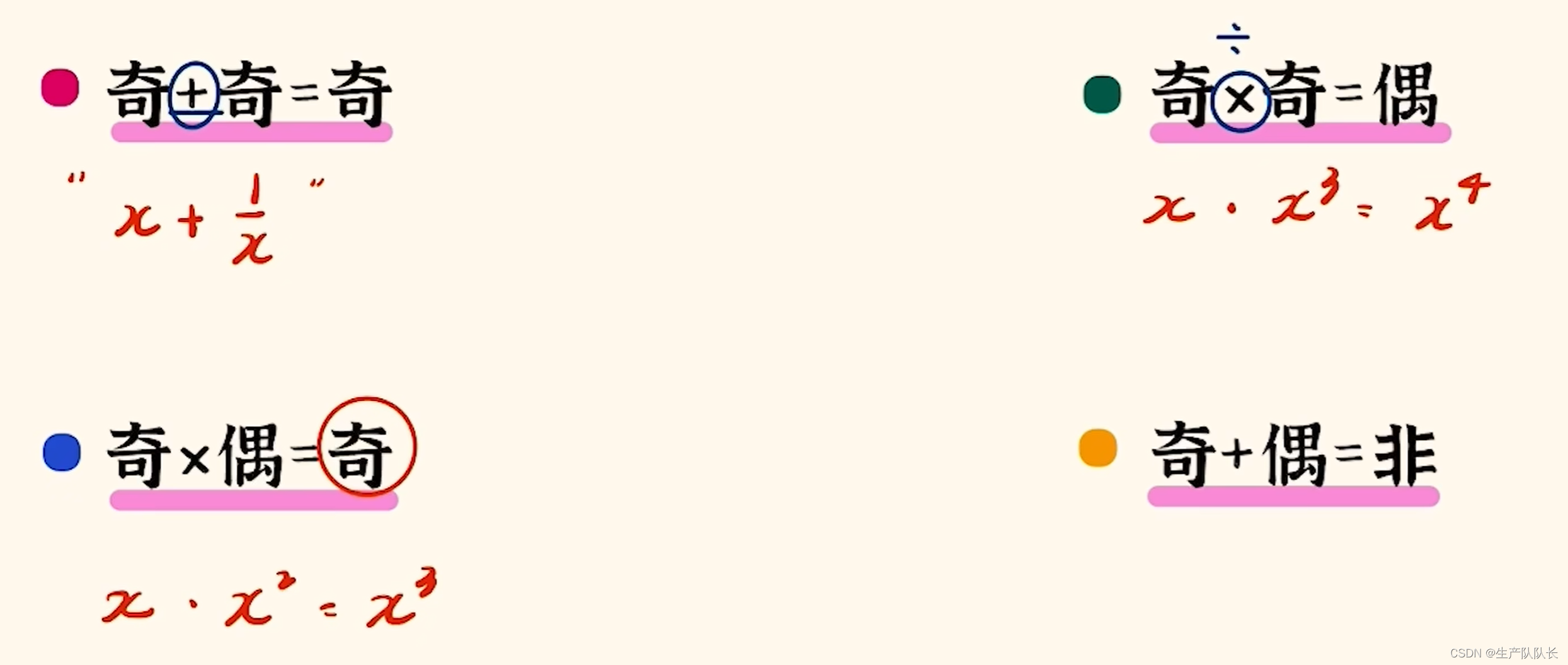
五、常見題型

1、判斷函數奇偶性

解題思路：
1、先求函數定義域，判斷定義域是否關于原點對稱
2、根據圖像或者定義，判斷函數的奇偶性（需要一定的因式分解的能力）
例題：
此題，無法畫圖，所以，根據定義來判斷奇偶性。

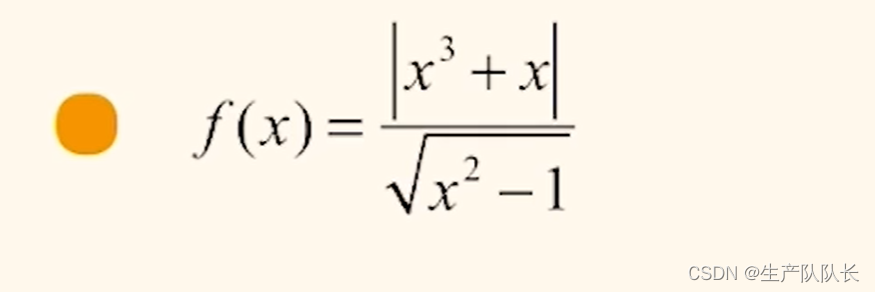
2、已知奇偶性，求參數

解題思路：
1、觀察定義域法
2、定義法
3、帶特殊值法
例題1：
該題，直接利用奇函數在x=0的值為0，代入f(x)，即可，求出的值。

例題2：
該題，帶特殊值法，解方程即可求出參數a的值。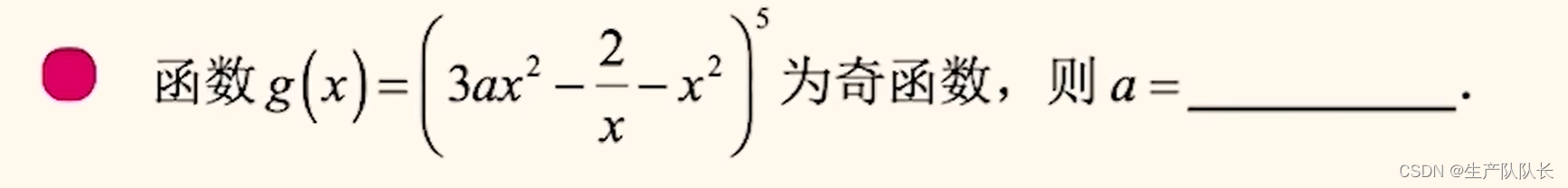例題3：
該題，根據奇偶函數的定義域必然關于原點對稱，求出參數a的值。進而，求出b的值。

例題4：
該題，根據奇偶函數的定義域必然關于原點對稱，求出a的值
可以發現，f(x)的分母中，x≠1，進而，求出a的值

3、已知奇偶性，求解析式

解題思路：
1、求誰設誰
2、聯立方程組
例題1：
該題，求x<0時的解析式和x=0時的解析式。

例題2：
根據定義，聯立方程組求解。