相應仿真原件請移步資源下載

LCL濾波器

LCL濾波器因其本身為一個二階系統，其本身就會引發諧振，導致相應諧振頻率處的增益得到放大，進而產生諧波等問題；另一方面，在弱電網下，逆變器會與電網阻抗發生耦合，進而造成多諧振峰現象，其更會影響系統的穩定性。

開環諧振機理

光伏并網系統的諧波源有來自于逆變器系統本身，還有來自于電網環境，以及逆變器自身諧波源與電網背景諧波源之間均存在交互作用，這種交互作用會加劇各逆變器輸出并網電流和公共并網節點處電壓的畸變，甚至會引起各逆變器之間以及逆變器與電網之間的諧振，并導致系統不穩定。

①逆變器本身的諧波源激勵引起的諧振；

逆變器本身諧波源激勵下并網接口等效電路如下圖：

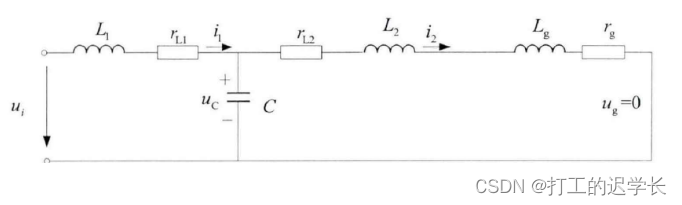
?進而得到其傳遞函數

畫出其波特圖

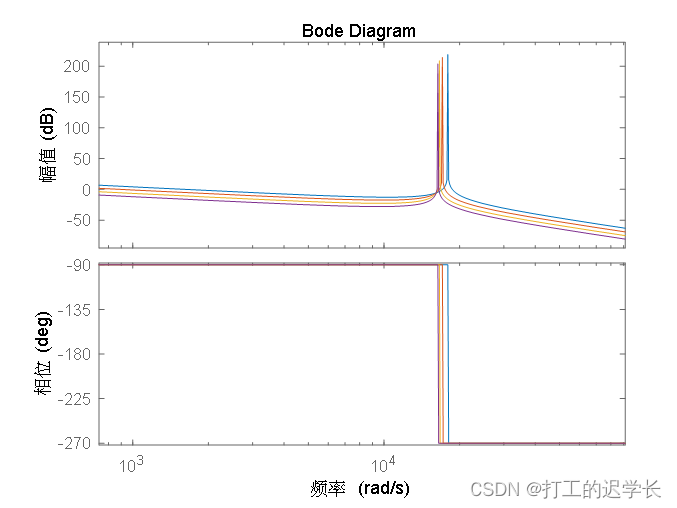
可以看到，隨著其電網阻抗的增加，諧振峰逐漸向低頻移動，故隨著電網越來越弱，其更容易產生低頻諧振，電流畸變的可能性越大。

②網側的諧波源激勵引起的諧振；

電網背景諧波源激勵下的并網接口電路如下：

進而可以得到其傳遞函數

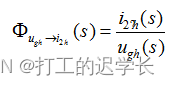
畫出其波特圖

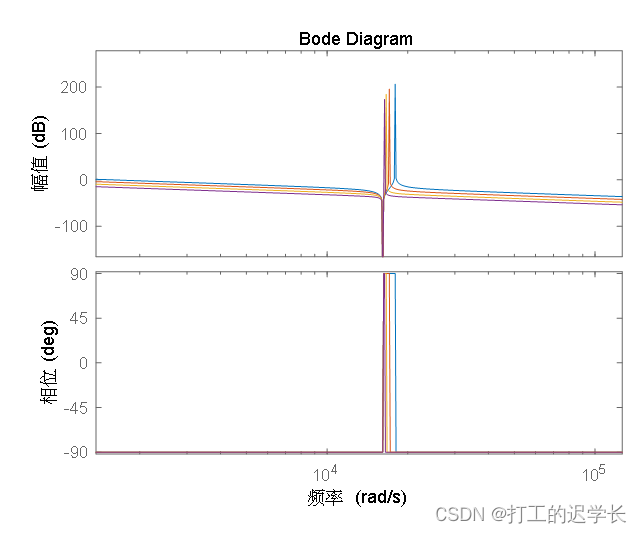
在與正的諧振尖峰頻率點相同頻率的電網背景諧波激勵下，LCL并網接口網絡就會發生諧振，而與負的衰減尖峰率點相同頻率的電網背景諧波將被衰減到很小，使其對并網接口電路輸出電流不構成影響。?

?隨著傳輸線電抗的增加，正的諧振尖峰頻率點向低頻方向偏移，此時電路網絡產生低頻諧振的可能性增加。

故對整個系統來說，隨著電網阻抗的增加，諧振峰逐漸向低頻移動，電流波形畸變的可能性更大。

具體的傳函推導過程以及波特圖源代碼請移步咸魚：電力電子打工魂