快速冪（求解原理+例題）

反復平方法（快速冪）：

代碼：?

例題：快速冪求逆元

作用：

????????快速求出? $a^k \ mod \ p$ ?的結果。

時間復雜度：

????????O(logk)

? ? ? ? 如果使用一般做法，從1循環到k，時間復雜度是O(k)

反復平方法（快速冪）：

? ? ? ? 將? $k$ ?用二進制表示： $(k)_{10}=(....)_2$

? ? ? ? 那么?? $k = 2^{x_1}+2^{x_2} + ... +2^{x_t}\ \ \ x_t<=log_2k$

? ? ? ? 因此?? $a^k \ =\ a^{2^{x_1}+2^{x_2}+...+2^{x_t}} \ \ \ x_t<=log_2k$

? ? ? ? 我們可以把? $a^k$ ?拆分成?? $a^k \ =\ a^{2^{x_1}} * a^{2^{x_2}} *... * a^{2^{x_t}} \ \ \ x_t<=log_2k$ ?

? ? ? ? 因此我們只需要預處理出下面的，就可以解決上述方法:

????????? $a^{2^0} \ mod \ p\\a^{2^1} \ mod\ p\\a^{2^2}\ mod\ p\\.\\.\\a^{2^{logk}}\ mod \ p$

? ? ? ? 如何求解這些需要預處理：

? ? ? ? 每次乘2

????????

qmi(long a,long k,long p){long res = 1;while(k!=0){if((k&1)==1) res = res*a%p; // 如果該位是1k = k>>1; // 右移一位a = a*a%p; //每次乘2}System.out.println(res);
}

? ? ? ? ?該代碼使用了一種位運算技巧。

????????位運算---求n的二進制表示中第k位是1還是0 (lowbit)-CSDN博客

例子：

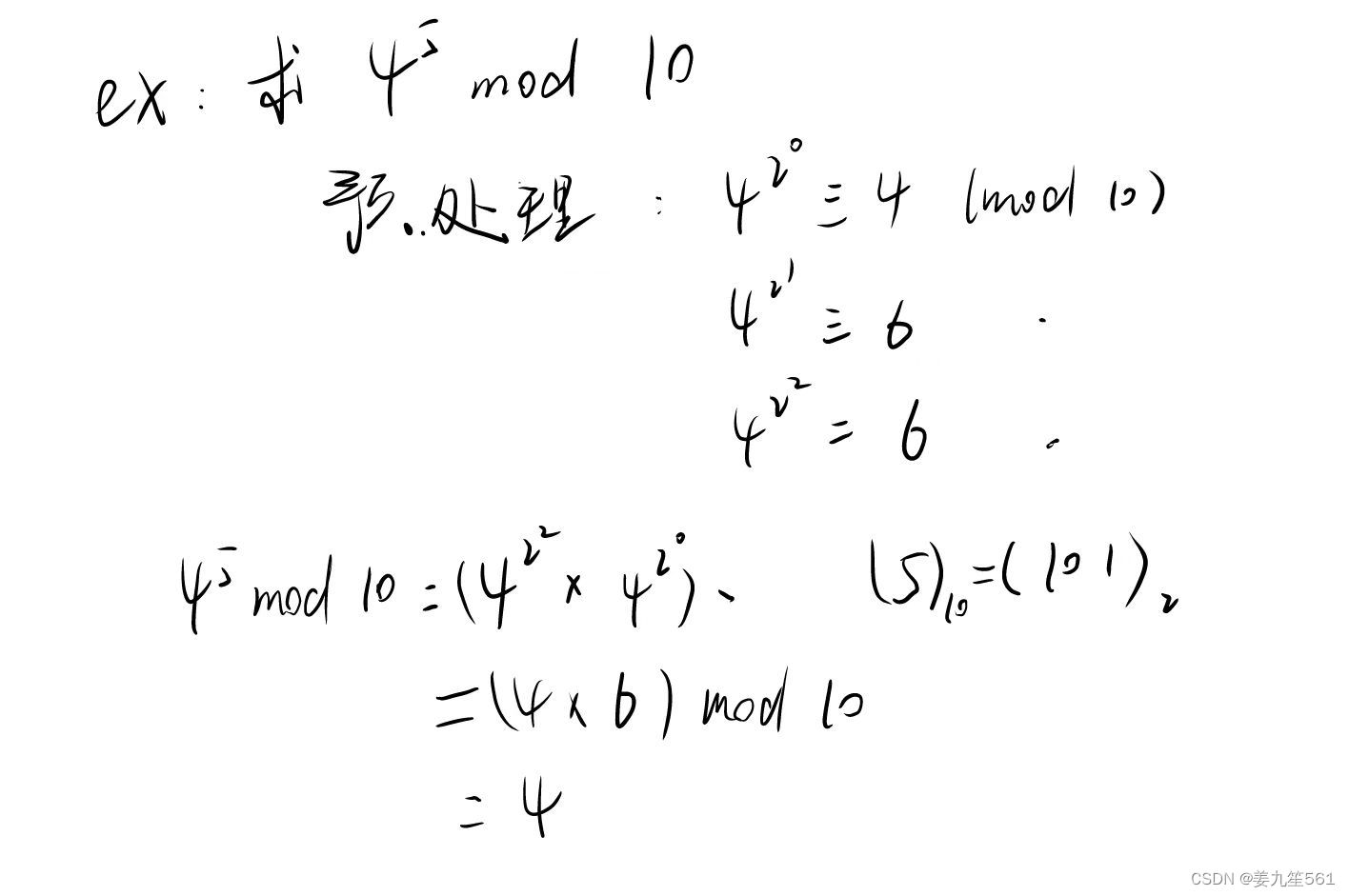
標準例題代碼：?

給定?n 組?ai,bi,pi，對于每組數據，求出? $a_i^{b_i}\ mod\ p_i$ 的值。

輸入格式

第一行包含整數?n。

接下來?n?行，每行包含三個整數?ai,bi,pi。

輸出格式

對于每組數據，輸出一個結果，表示? $a_i^{b_i}\ mod\ p_i$ 的值。

每個結果占一行。

數據范圍

1≤n≤100000,
1≤ai,bi,pi≤2×10^9

輸入樣例：
2
3 2 5
4 3 9
輸出樣例：
4
1

import java.util.*;
import java.io.*;class Main{static final int N = 100010;static int n;public static void main(String[] args) throws IOException{BufferedReader in = new BufferedReader(new InputStreamReader(System.in));n = Integer.parseInt(in.readLine());while(n-->0){String[] s = in.readLine().split(" ");long a = Long.parseLong(s[0]);long b = Long.parseLong(s[1]);long p = Long.parseLong(s[2]);qmi(a,b,p); // 快速冪}}public static void qmi(long a,long b,long p){long res = 1;while(b!=0){if((b&1)==1) res = res*a%p; // 如果該位是1b = b>>1; // 右移一位a = a*a%p; //每次乘2}System.out.println(res);}
}

例題：快速冪求逆元

? ? ? ? 費馬定理。

給定?n?組?ai,pi，其中?pi?是質數，求?ai?模?pi?的乘法逆元，若逆元不存在則輸出?impossible。

注意：請返回在?0～p?1?之間的逆元。

乘法逆元的定義

若整數?b，m 互質，并且對于任意的整數?a，如果滿足?b|a，則存在一個整數?x，使得 $\frac{a}{b}\equiv a*x\ (mod \ m)$ ，則稱?x?為?b?的模?m?乘法逆元，記為? $b^{-1}\ (mod\ m)$ 。

b?存在乘法逆元的充要條件是?b?與模數?m?互質。當模數?m?為質數時， $b^{m-2}$ ?即為?b?的乘法逆元。

輸入格式

第一行包含整數?n。

接下來?n?行，每行包含一個數組?ai,pi，數據保證?pi?是質數。

輸出格式

輸出共?n?行，每組數據輸出一個結果，每個結果占一行。

若?ai?模?pi?的乘法逆元存在，則輸出一個整數，表示逆元，否則輸出?impossible。

數據范圍

1≤n≤10^5,
1≤ai,pi≤2?10^9

輸入樣例：
3
4 3
8 5
6 3
輸出樣例：
1
2
impossible

解決方法：

????????? $\frac{a}{b}\equiv a*x\ (mod \ m)$

? ? ? ?由題意可知：? $\frac{a}{b}\equiv a*b^{-1}\ (mod \ m)$

???????? ${a}\equiv a*b*b^{-1}\ (mod \ m)$

???????? $b*b^{-1}\equiv 1\ (mod \ m)$

????????x?為?b?的模?m?乘法逆元，記為? $b^{-1}\ (mod\ m)$ ，因此? $b*x\equiv 1\ (mod \ m)$

? ? ? ? 由費馬定理可知：

?????????????????????????????????????????????? $b^{p-1}\ \equiv \ 1\ (mod\ p)\\b*b^{p-2} \ \equiv \ 1\ (mod\ p)$

? ? ? ? 因此， $x = b^{p-2}\ (mod \ p)$

? ? ? ? 再使用快速冪解決：

import java.util.*;
import java.io.*;
class Main{static int n;public static void main(String[] args) throws IOException{BufferedReader br = new BufferedReader(new InputStreamReader(System.in));n = Integer.parseInt(br.readLine());while(n-->0){String[] s = br.readLine().split(" ");int a = Integer.parseInt(s[0]);int p = Integer.parseInt(s[1]);long res = qmi(a,p-2,p);if(a%p==0) System.out.println("impossible");else System.out.println(res);}}public static long qmi(int a,int k,int p){long res = 1;while(k!=0){if((k&1)==1) res = res*a%p;k = k>>1;a = (int)((long)a*a%p);}return res;}
}

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/718389.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/718389.shtml
英文地址，請注明出處：http://en.pswp.cn/news/718389.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！