1049.最后一塊石頭的重量II

有一堆石頭，每塊石頭的重量都是正整數。

每一回合，從中選出任意兩塊石頭，然后將它們一起粉碎。假設石頭的重量分別為?x 和?y，且?x <= y。那么粉碎的可能結果如下：

如果?x == y，那么兩塊石頭都會被完全粉碎；

如果?x != y，那么重量為?x?的石頭將會完全粉碎，而重量為?y?的石頭新重量為?y-x。

最后，最多只會剩下一塊石頭。返回此石頭最小的可能重量。如果沒有石頭剩下，就返回 0。

示例：

• 輸入：[2,7,4,1,8,1]
• 輸出：1

解釋：

• 組合 2 和 4，得到 2，所以數組轉化為 [2,7,1,8,1]，
• 組合 7 和 8，得到 1，所以數組轉化為 [2,1,1,1]，
• 組合 2 和 1，得到 1，所以數組轉化為 [1,1,1]，
• 組合 1 和 1，得到 0，所以數組轉化為 [1]，這就是最優值。

提示：

• 1 <= stones.length <= 30
• 1 <= stones[i] <= 1000

本題要求最小的石頭重量，最好的情況就是最后剩下的兩個石頭重量一致，結果為0。那也就跟昨天的分割子集的本質一樣，將這個數組分割成兩個子集，使得兩個子集的元素和相等。因此看是否可以將石頭重量集合拆分為總和為sum/2的子集。因為本題石頭粉碎是不可逆的，因此屬于01背包問題，那么就開始對應如下四點：

• 背包的可容納的重量為sum / 2
• 背包要放入的石頭的重量也就是石頭的價值
• 背包如果正好裝滿，說明找到了總和為 sum / 2 的子集。
• 背包中每一個元素是不可重復放入

動規五部曲：

1. 確定dp數組以及下標的含義：dp[j]表示重量為j的背包，最多可以背的重量為dp[j]
2. 確定遞推公式：dp[j]=max(dp[j], dp[j-stones[i]]+stones[i])
3. dp數組如何初始化：sum+=stones[i] target=sum/2
4. 遞歸順序：先遍歷石頭，再遍歷重量，并且重量要倒序遍歷

如果背包需要滿足的容量為target，當dp[target]==target時，背包就裝滿了，也就是本題的結果為0。如果不能滿足，因為sum/2是向下取整，所以sum-dp[target]一定大于dp[target]，所以相撞以后剩下的石頭重量為(sum-dp[target])-dp[target]

class Solution {public int lastStoneWeightII(int[] stones) {int sum=0;for(int i=0;i<stones.length;i++){sum+=stones[i];}int target=sum>>1;int[] dp= new int[target+1];for(int i=0;i<stones.length;i++){for(int j=target;j>=stones[i];j--){dp[j]=Math.max(dp[j], dp[j-stones[i]]+stones[i]);}}return (sum-dp[target])-dp[target]; }
}

注意：這里不需要再單獨判斷一下dp[target]是否等于target了，如果等于的話，其實最后相當于sum-2*target=0了，如果多寫了這一步判斷，反而會漏算情況。

并且sum/2的空間復雜度要比sum>>1，移位運算高，所以最好寫后者。

494.目標和

給定一個非負整數數組，a1, a2, ..., an, 和一個目標數，S。現在你有兩個符號?+?和?-。對于數組中的任意一個整數，你都可以從?+?或?-中選擇一個符號添加在前面。

返回可以使最終數組和為目標數 S 的所有添加符號的方法數。

示例：

• 輸入：nums: [1, 1, 1, 1, 1], S: 3
• 輸出：5

解釋：

• -1+1+1+1+1 = 3
• +1-1+1+1+1 = 3
• +1+1-1+1+1 = 3
• +1+1+1-1+1 = 3
• +1+1+1+1-1 = 3

一共有5種方法讓最終目標和為3。

提示：

• 數組非空，且長度不會超過 20 。
• 初始的數組的和不會超過 1000 。
• 保證返回的最終結果能被 32 位整數存下。

這道題先用動態規劃五部曲想了一下：本題依然是只能取一次，所以還是01背包思路

1. 確定dp數組以及下標的含義：dp[j]表示達到和為j的值有dp[j]種方法
2. 確定遞推公式：目前還不知道
3. dp數組如何初始化：dp[0]=1，因為當只有1個元素的時候，那么就只有一種方法
4. 確定遍歷順序：還是按照元素從前向后，按照數值從后向前
5. 舉例推導dp數組：遞推公式還沒出來，暫時舉不出來例子

腦子比較累，直接看了題解：

本題要如何使表達式結果為target。首先因為有sum，所以left + right = sum，sum是固定的，因此right = sum - left。既然為target，那么就一定有? left組合 - right組合 = target，這里left就是加法的總和，right就是減法的總和，公式來了， left - (sum - left) = target 推導出 left = (target + sum)/2, target是固定的，sum是固定的，left就可以求出來。此時問題就是在集合nums中找出和為left的組合。此時問題就轉化為，裝滿容量為left的背包，有幾種方法。還要注意幾種特殊的情況：(target + sum) / 2 應該擔心計算的過程中向下取整有沒有影響，如果sum為5，target為2，那么無論怎樣也不會到達target值，也就是說當sum+target為奇數時，是沒有解決方案的。并且如果target的的絕對值大于sum，也是沒有解決方法的，直接返回0。

只要搞到nums[i]，湊成dp[j]就有dp[j - nums[i]] 種方法。

例如：dp[j]，j 為5，

• 已經有一個1（nums[i]） 的話，有 dp[4]種方法 湊成 容量為5的背包。
• 已經有一個2（nums[i]） 的話，有 dp[3]種方法 湊成 容量為5的背包。
• 已經有一個3（nums[i]） 的話，有 dp[2]中方法 湊成 容量為5的背包
• 已經有一個4（nums[i]） 的話，有 dp[1]中方法 湊成 容量為5的背包
• 已經有一個5 （nums[i]）的話，有 dp[0]中方法 湊成 容量為5的背包

那么湊整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起來。

所以求組合類問題的公式，都是類似這種：dp[j] += dp[j - nums[i]]

import java.lang.Math;
class Solution {public int findTargetSumWays(int[] nums, int target) {int sum=0;for(int i=0;i<nums.length;i++){sum+=nums[i];}int left=(sum+target)>>1;if((sum+target)%2==1) return 0;if(Math.abs(target)>sum) return 0;int[] dp= new int[left+1];dp[0]=1;for(int i=0;i<nums.length;i++){for(int j=left;j>=nums[i];j--){dp[j]+= dp[j-nums[i]];}}return dp[left];}
}

474.一和零

給你一個二進制字符串數組 strs 和兩個整數 m 和 n 。

請你找出并返回 strs 的最大子集的大小，該子集中 最多 有 m 個 0 和 n 個 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

示例 1：

• 輸入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3

• 輸出：4

• 解釋：最多有 5 個 0 和 3 個 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。 其他滿足題意但較小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不滿足題意，因為它含 4 個 1 ，大于 n 的值 3 。

示例 2：

• 輸入：strs = ["10", "0", "1"], m = 1, n = 1
• 輸出：2
• 解釋：最大的子集是 {"0", "1"} ，所以答案是 2 。

提示：

• 1 <= strs.length <= 600
• 1 <= strs[i].length <= 100
• strs[i]?僅由?'0' 和?'1' 組成
• 1 <= m, n <= 100

本題還是一個背包問題，本題中strs 數組里的元素就是物品，每個物品都是一個，只能取一次，因此還是01背包問題。這里限制了兩個元素的大小，這兩個大小之間是沒有什么制約關系的，相當于有兩個背包，所以要定義一個二維dp數組dp[i][j]繼續開始動規五部曲：

1. 確定dp數組以及下標的含義：dp[i][j]表示最多取i個1和j個0后的最大子集的大小
2. 確定遞推公式：dp[i][j]是由前一個已經選好的子串推導而來，假設前面那個子串已經有zero個0和one個1，那么dp[i][j]=dp[i-zero][j-one]+1，并且還要跟自己做比較，取最大值。
3. dp數組如何初始化：初始化為0
4. 確定遍歷順序：遍歷物品要從前往后，遍歷背包要從后往前，這里m和n都是背包，所以都是從后往前遍歷。
5. 舉例推導dp數組：以輸入：["10","0001","111001","1","0"]，m = 3，n = 3為例，最后dp數組的狀態如下所示：
   ?

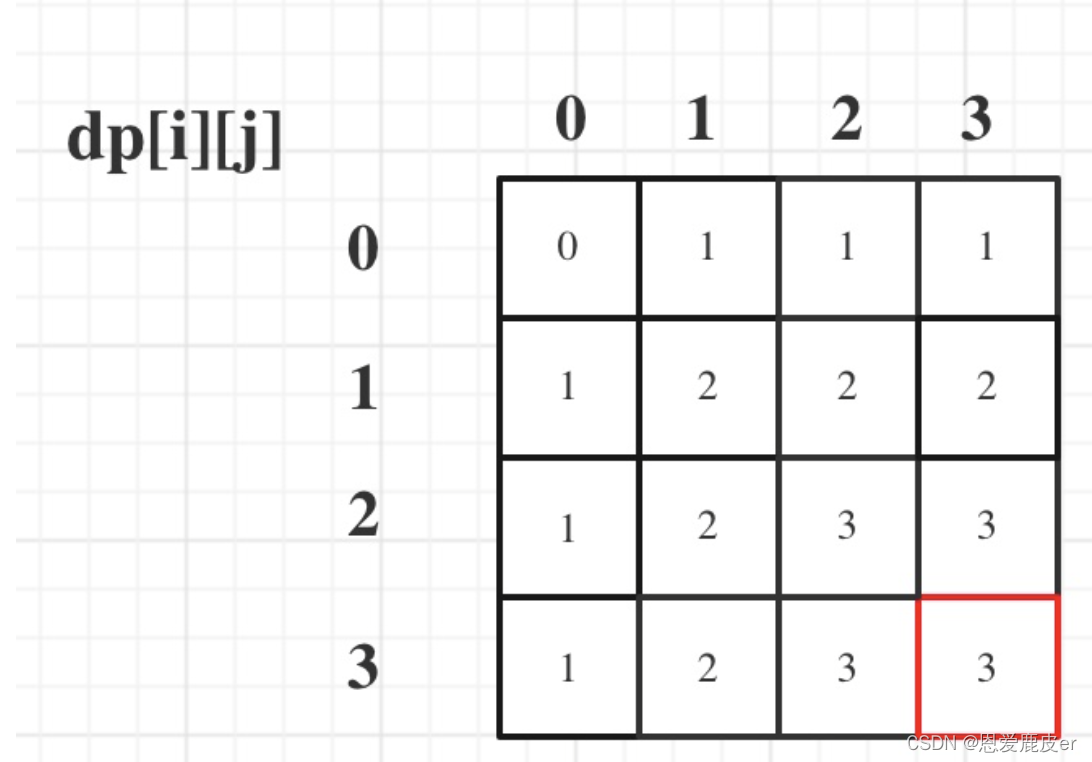
class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][] dp = new int[m+1][n+1];for(String str:strs){int zero=0, one=0;for(char c : str.toCharArray()){if(c =='0') zero++;else one++;}for(int i=m;i>=zero;i--){for(int j=n;j>=one;j--){dp[i][j]=Math.max(dp[i][j], dp[i-zero][j-one]+1);}}}return dp[m][n];}
}