KNN和Kmeans

KNN

KNN-K個最近的鄰居，而K是可人先預設出來的。
所謂近朱者赤，近墨者黑。
可以選取離當前最近的K個樣本來作為輔助判斷，因為本樣本和最近的K個樣本應該是處于一種相似的狀態。
以下是一個蘋果和梨的識別任務。
圖上會出現一個未知的事物，可以結合和根據以往已經出現在圖上的數據來對這個未知事物進行判斷。

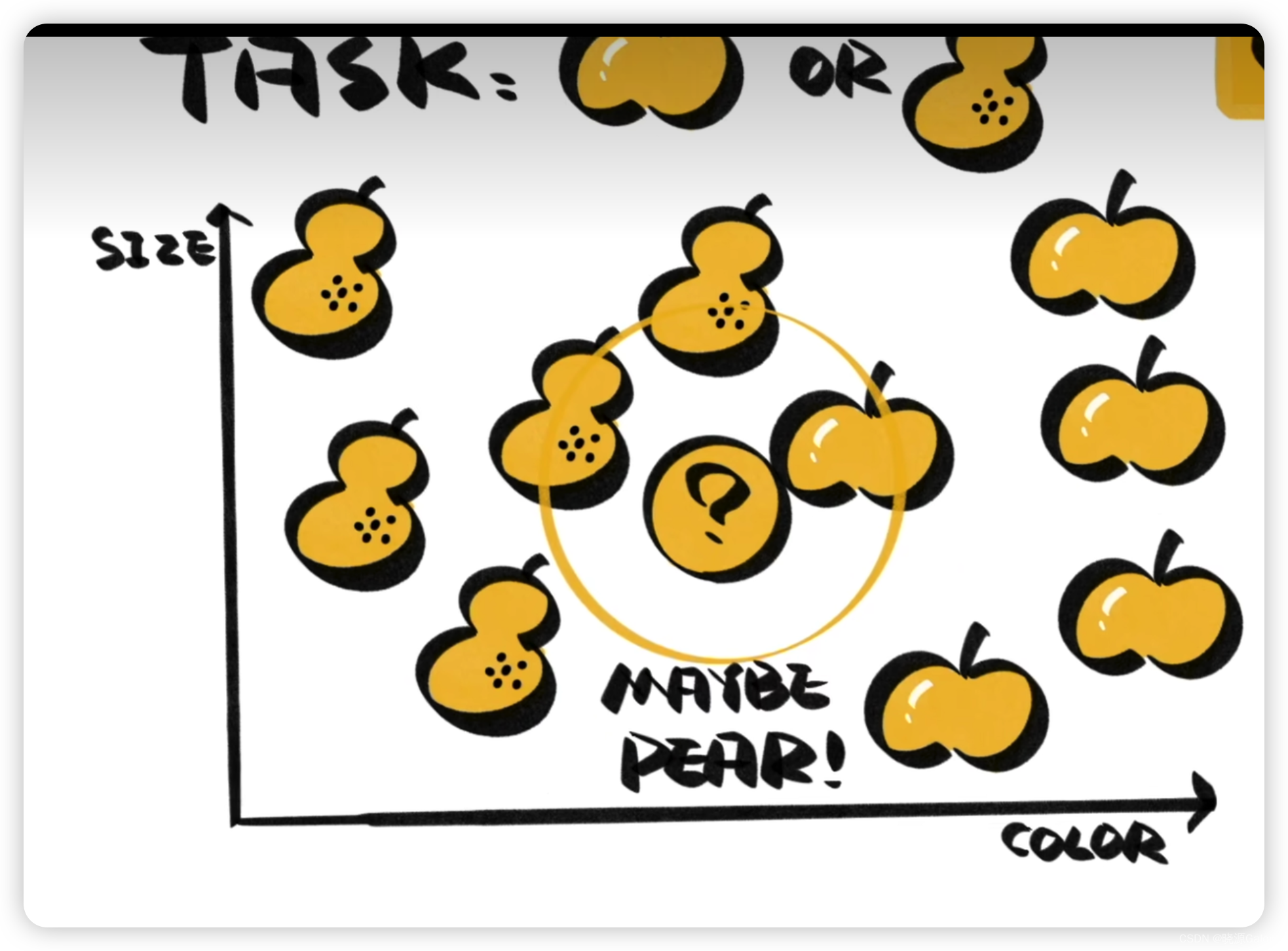
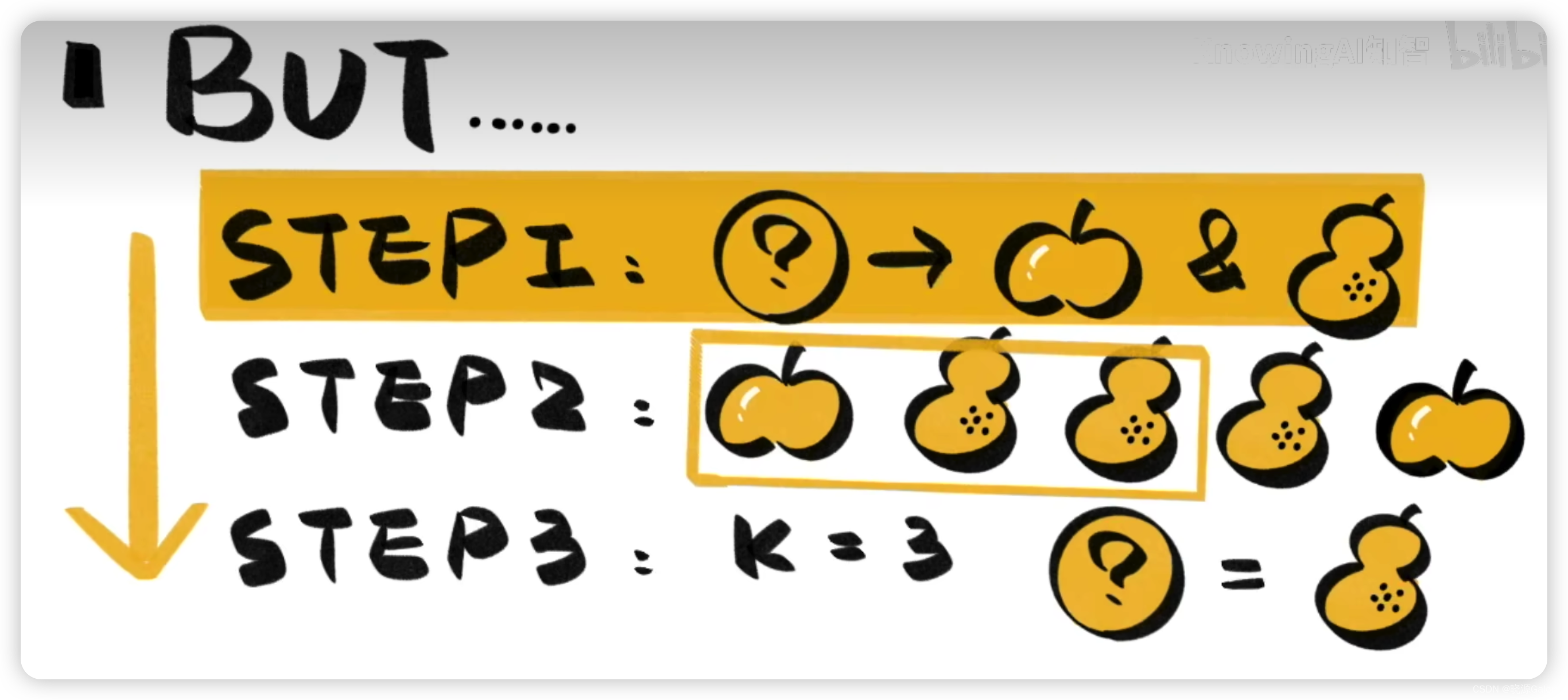
可以選取離這個樣本最近的K個樣本進行判斷，比如上圖，讓K=3，離樣本最近的3個樣本有兩個梨子，1個蘋果。那么當前樣本可能會被判斷為梨子。
而關于最近的近也有不同的衡量來源，比如說曼哈頓距離和歐式距離。

K的選取

如果說K選取過小，則最近的樣本的影響相對較大，若這個最近樣本是一個特殊的樣本，將被容易帶偏。
如果說K選取過大，則如果樣本數本身不夠大的情況下，容易將偏遠樣本的信息也囊括進來，容易受到相關影響。

KNN算法的應用

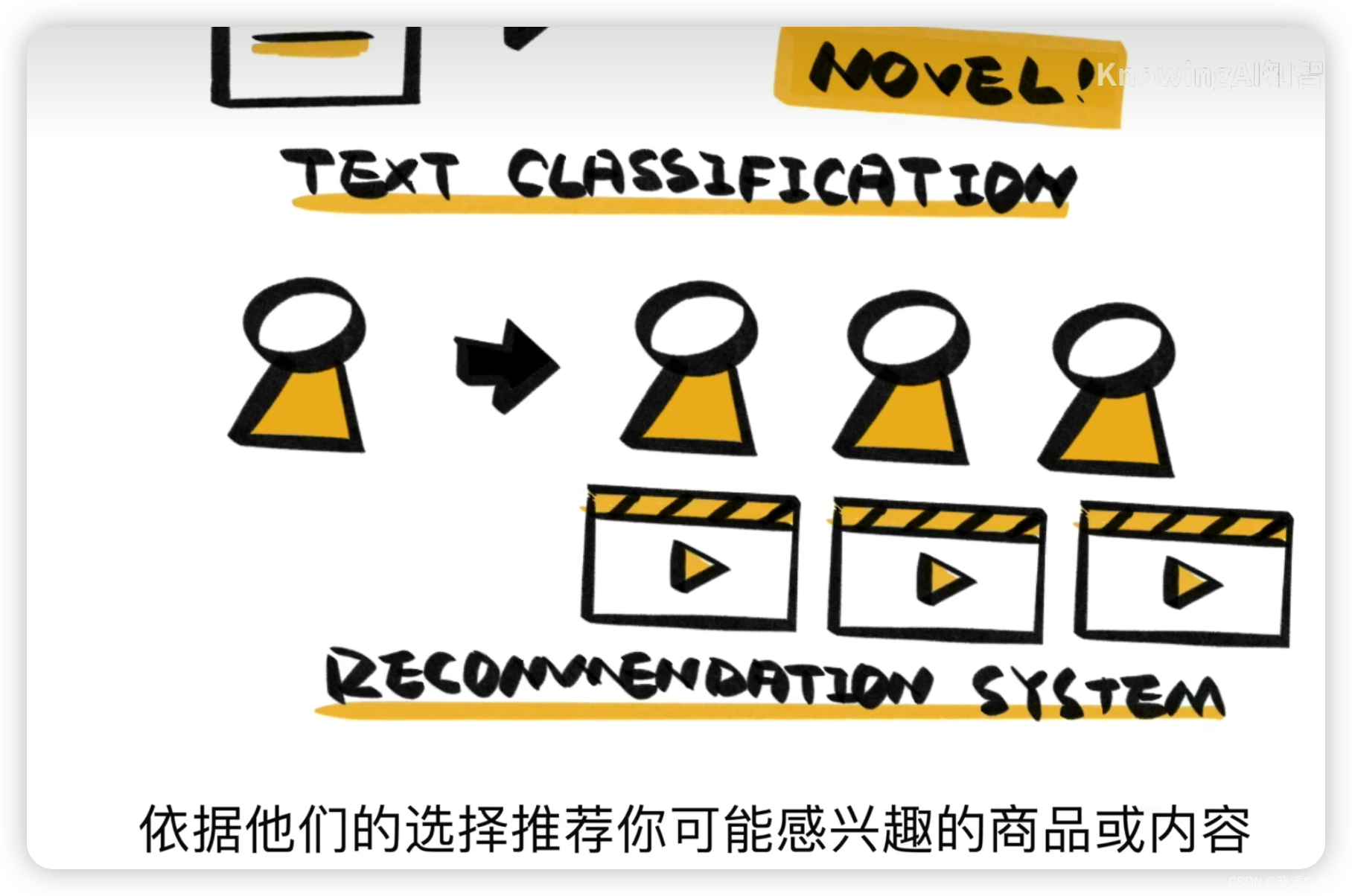
比如在推薦算法中，可以將用戶和他在空間上相近的角色進行比對，從而得到相近的信息，來作為當前用戶的特征，從而結合這個特征找到符合的商品來進行推送。

由于KNN一個新樣本，需要和其他樣本進行計算。計算本身會帶來損耗。同時計算本身是受到K的大小和特征維度的影響。

Kmeans

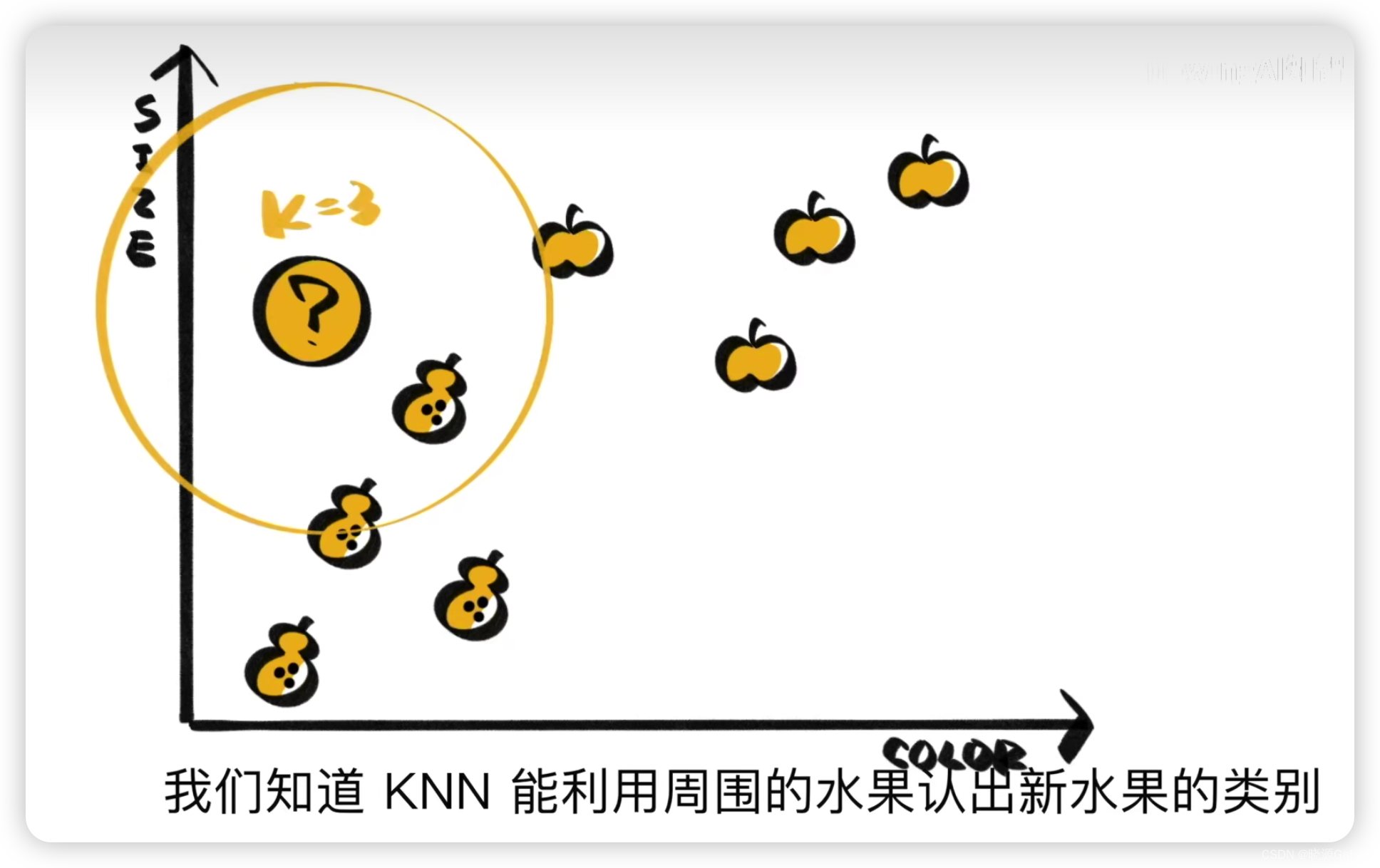
KNN是通過周圍K個水果來認出當前水果。

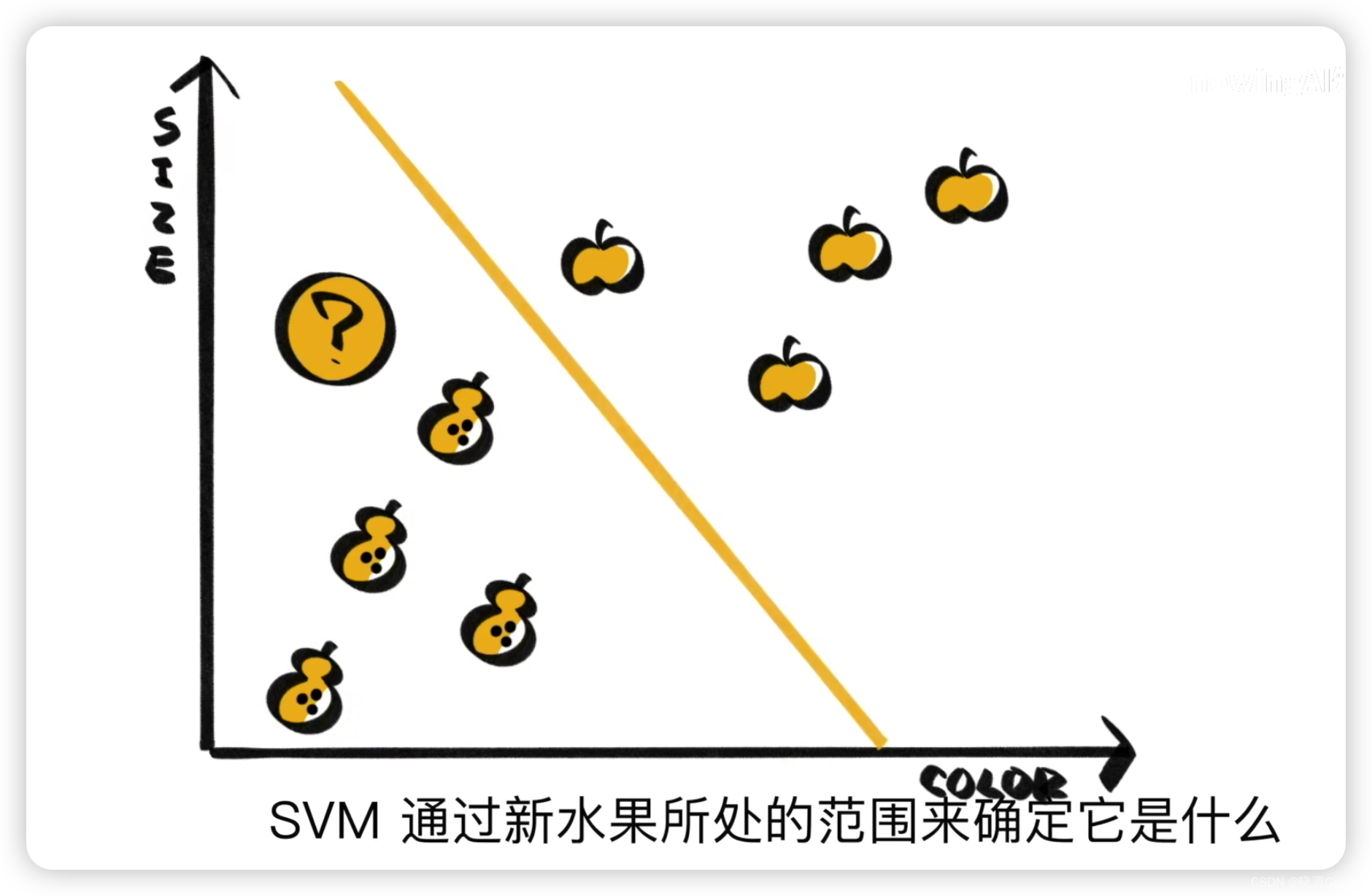
而SVM可以通過劃分好的直線來將水果區分開，只需看水果落入的是哪一個范圍，就可認為是哪一種水果。（實際處理中可能涉及到軟間隔的影響）
而不管是KNN還是SVM，都是建立在已有標簽的樣本的數據之上。（KNN中的K個樣本是需要知道這K個樣本到底是啥，而SVM需要知道一些具有標簽的樣本，從而來畫出能夠區分開的線）

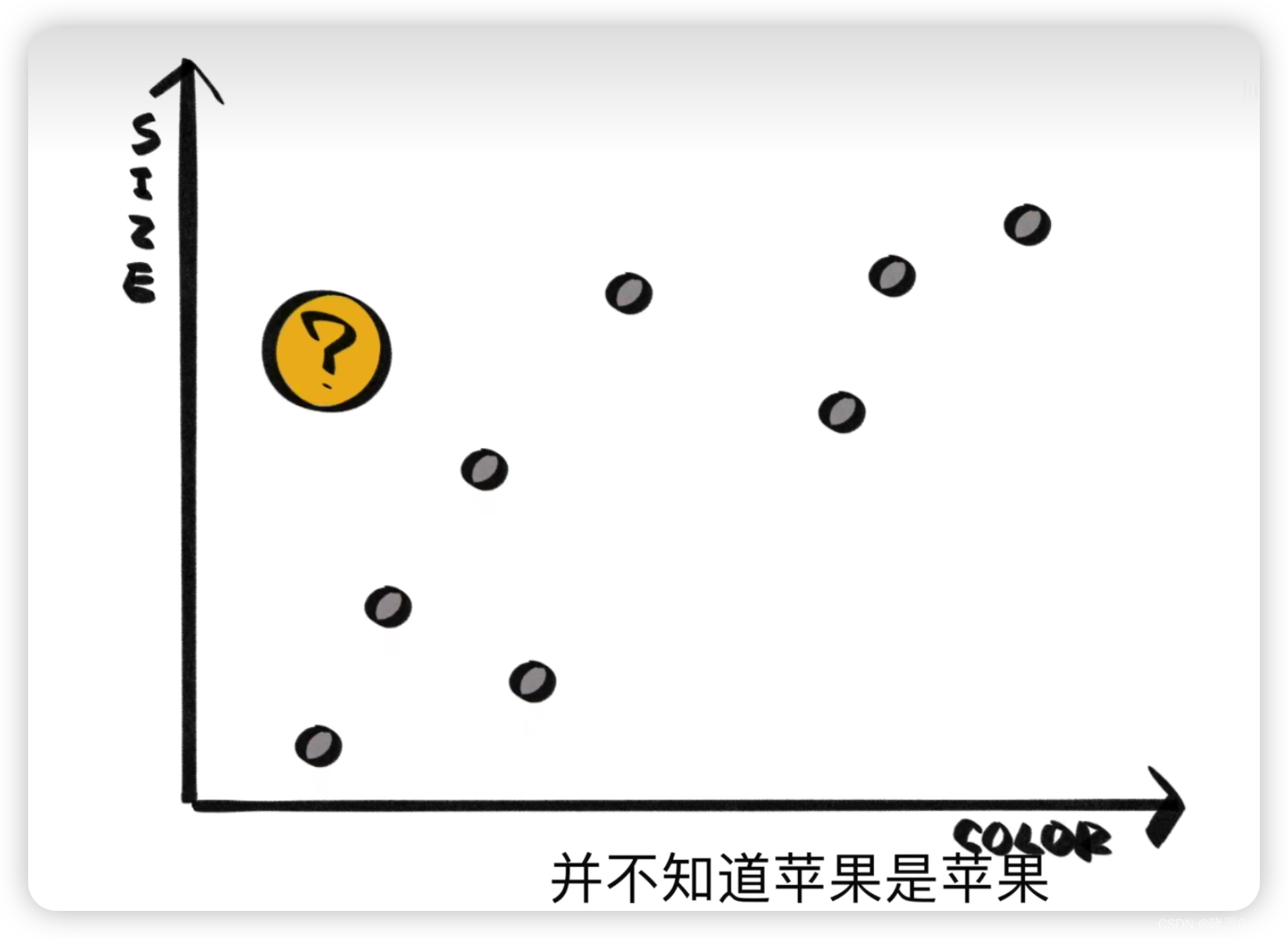
而只知道樣本分布，不知道樣本具體是啥的時候就需要用到Kmeans。
可以人為設置具體要分為幾類，從而讓Kmeans確認出最終各個點的歸屬。
打個比方，就好像有一片居民居住地，作為城市規劃的專家，你要設置幾個村中心，并將哪些人劃分到這個村落中去來進行管理。
如果這個人居住地和某個村中心A相距比另一個村中心B來得更遠，那么這個人應該被劃分到村中心B中去。
也就是說，可以先認為離誰近就可以歸于誰。

Kmeans步驟

可以粗略歸納為——選取樣本中心->各點計算距離來歸于某一個樣本中心->不斷迭代，直至樣本中心穩定。

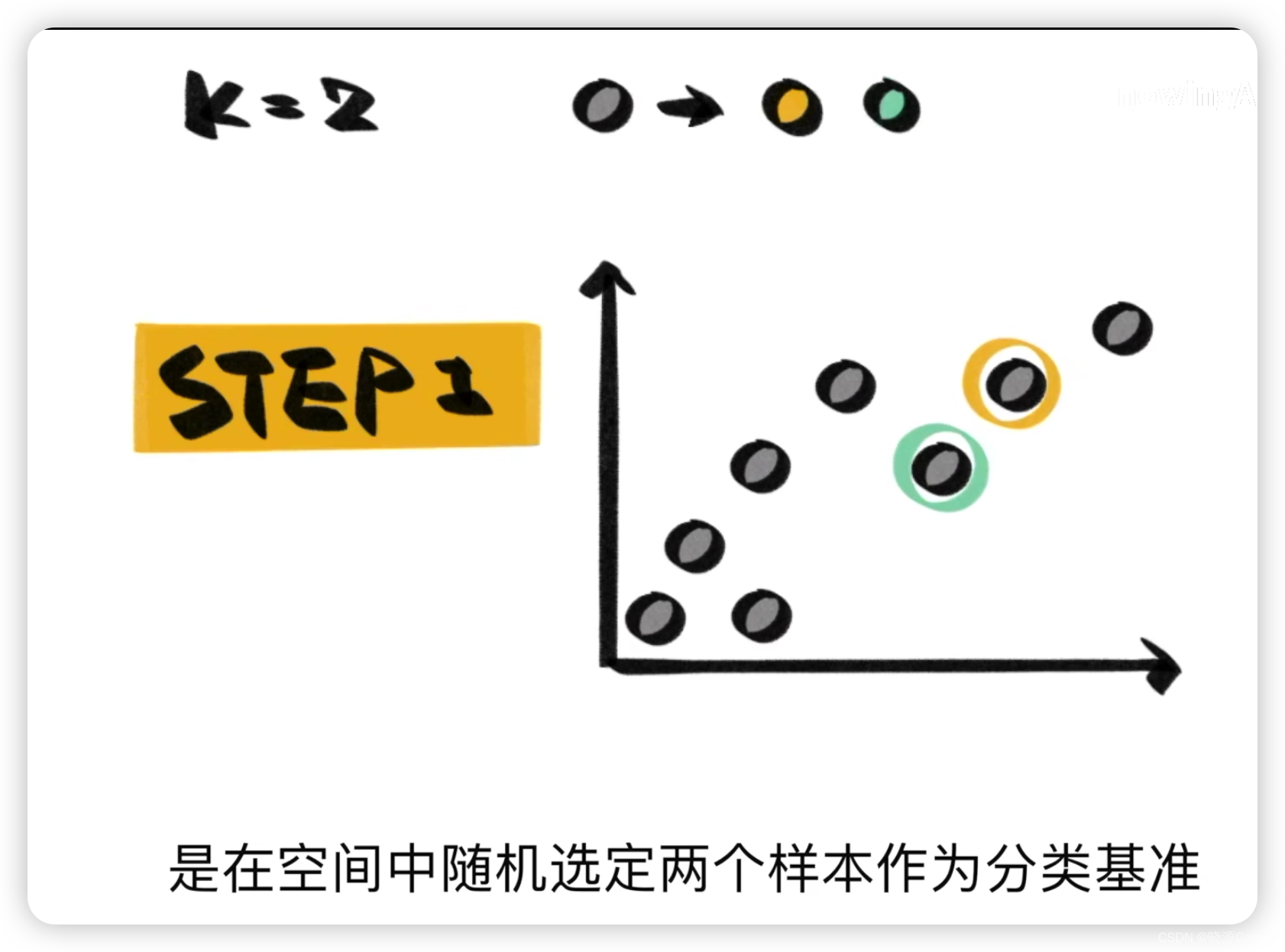
首先在圖中隨機找到兩個點來作為樣本中心（因為K=2，所以挑兩個點）。
然后每一個點計算與這兩個樣本點的距離，從而來進行歸類。
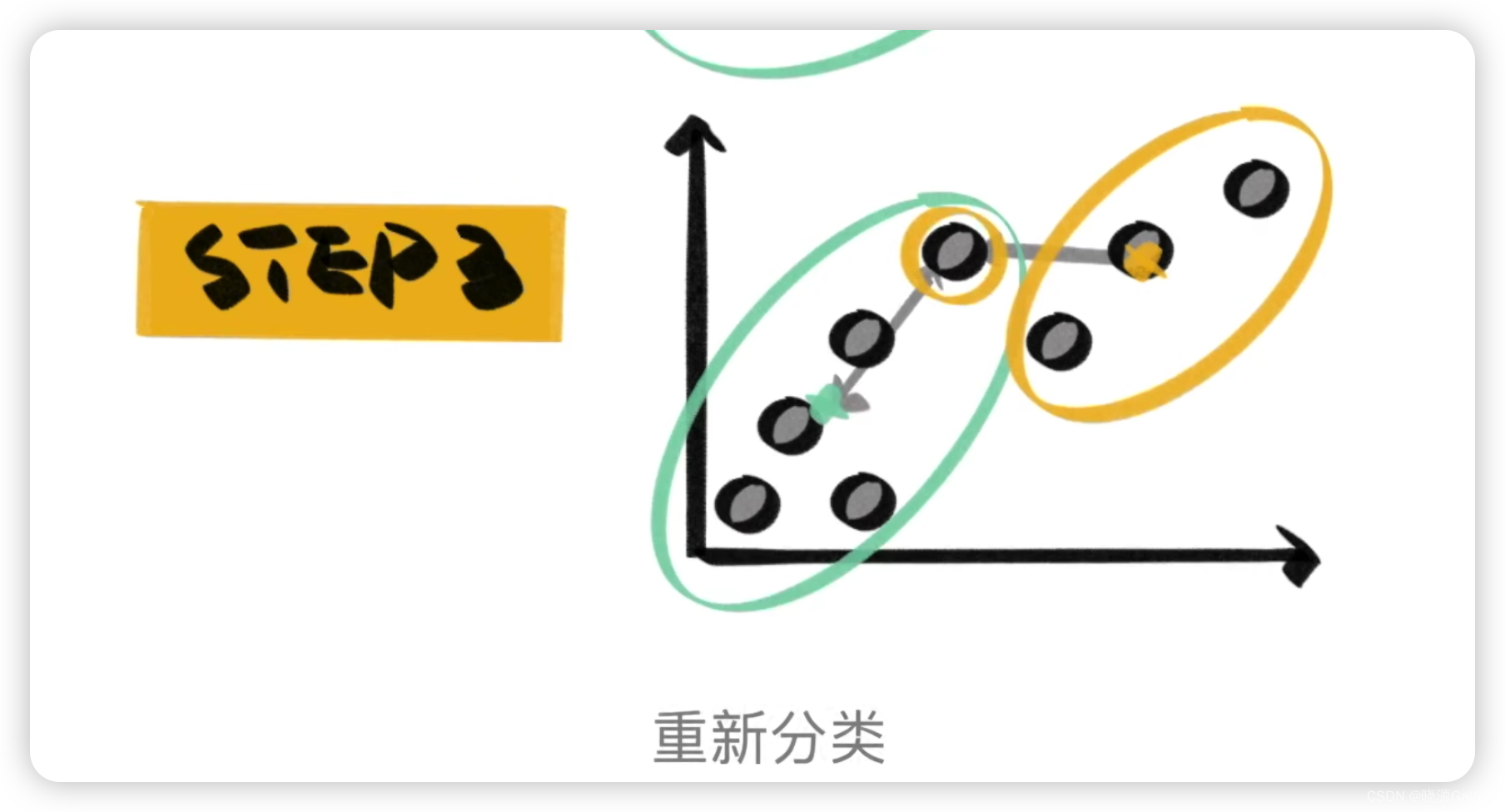
然后每一個點都計算出來到底歸于哪一個類。
然后可以將類的點再取平均來作為這個類新的樣本中心。
然后所有點再與新的樣本中心進行計算，迭代，直至新的樣本中心，沒有再發生改變。
則可認為基本穩定。

所以Kmeans相對簡單，容易上手，是一種無監督學習（不需要樣本帶有標簽，只需要知道樣本的分布即可，打標簽是需要成本的，相關的工作可以在boss上面找到數據標注員的工作）。
而Kmeans也有缺點，比如效果并不一定比有監督學習來得好，并且效果比較依賴K的選取。